Lektsii / теория ОМД / Прямые задачи ОМД / Кузнечная протяжка

4

Кузнечная протяжка

Рассмотрим вторую наиболее распространенную операцию свободной ковки – кузнечную протяжку. При ковке крупных поковок стремятся “разбить” линейную структуру слитка, однако с помощью только операции осадки это сделать не удается. Достаточно равномерную “проработку’’слитка получают, комбинируя осадку и протяжку.

При протяжке увеличивается длина заготовки за счет уменьшения её поперечного сечения. Заготовка деформируется участками при последовательной подаче её под бойки.

После каждой подачи участок полосы обжимается бойками. Объём, который находится под непосредственным воздействием бойков, называется геометрическим очагом деформации. При протяжке на плоских бойках поковка кантуется на 90 вокруг продольной оси.

Кузнечная протяжка применяется при производстве роторов турбин, прокатных валков и других крупных деталей.

При кузнечной протяжке металл находится в весьма неблагоприятном напряженном и деформированном состоянии, вследствие чего возможно образование некоторых внутренних дефектов или развитие имеющихся несплошностей.

Следует отметить, что при благоприятных соотношениях размеров очага деформации ковка при определенных условиях способствует ликвидации дефектов металла.

Определим усилие деформирования при вытяжке на плоских бойках.

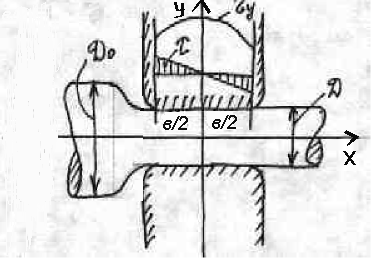
Примем допущение, что протяжка прямоугольного бруса при воздействии на него бойками по схеме приведенной на рисунке происходит в условиях плоской деформации. Это допущение будет тем ближе к действительности, чем меньше отношение ширины бойка к ширине поковки.

Значительное влияние на уширение оказывают недеформируемые части поковки, наличие которых, так же как высокие значения коэффициента трения, значительно уменьшают уширение металла при ковке.

При сделанном допущении протяжку можно рассматривать как случай плоского деформированного состояния и воспользоваться основными соотношениями для этого случая.

Для расчета усилия, развиваемого прессом, и удельного давления деформирования воспользуемся приближенным уравнением равновесия в виде (1.3).

Так как ширина бойка в обычно бывает меньше, чем двойная высота поперечного сечения, то есть , то, очевидно, эпюра контактных касательных напряжений состоит только из одного участка

Подставляем это значение в уравнение равновесия, интегрируем его совместно с условием пластичности

(1.28)

Причем последнее выражение предварительно упростим сделав допущение, что напряжение на площадках перпендикулярных к выбранным осям координат являются главными. Тогда соотношение (1.28) примет вид

(1.29)

где (для плоского деформированного состояния)

Дифференцируя (1.29), находим

(1.30)

Условие пластичности (1.30) в рассматриваемом случае является точным, поскольку касательное напряжение в этом случае не зависит от нормальных напряжений.

Его и интегрируем совместно с уравнением равновесия.

Определяя постоянную интегрирования при условии, что на границе контактной плоскости (при , где в ширина бойка) , имеем для нормального напряжения

(1.31)

То есть получили параболическую эпюру распределения вертикального контактного напряжения. Интегрирование по контактной площади бойка и поковки и деление на эту площадь дает для удельного давления протяжки следующее выражение

(1.32)

Полное усилие, развиваемое прессом

(1.33)

Здесь а и h – размеры сечения поковки.

Так как отношение в силу его малости не оказывает заметного влияния на величину удельного давления, а площадь контактной поверхности при протяжке будет максимальной в начале процесса протяжки поковки (или слитка), пресс для протяжки должен рассчитываться по исходному сечению слитка или поковки.

При вытяжке под вырезными бойками, часть поверхности которых цилиндрическая, для определения усилия и удельного давления деформирования можно воспользоваться приближенным дифференциальным уравнением равновесия в цилиндрических координатах в виде (с учетом поправочного коэффициента )

(1.34)

Здесь D – диаметр поковки.

Поправочный коэффициент учитывает то обстоятельство, что контактная поверхность бойков является только частью цилиндра с центральным углом .

Полагая, что ширина бойка меньше, чем двойной диаметр поковки, то есть , примем, что эпюра касательных напряжений на контактной поверхности по оси Х состоит только из одной нисходящей ветви, имея максимум на границе и нулевое значение в центре контактной поверхности.

Тогда интегрируя уравнение (1.34) совместно с уравнением (1.30) и определяя постоянную интегрирования С из условия, что при

,

находим

(1.35)

то есть параболическую эпюру нормальных контактных напряжений.

Для определения полного усилия протяжки необходимо вычислить интеграл

Подставляя значение из формулы (1.35) и производя интегрирование, находим

Замечая, что (где F – площадь проекции на горизонтальное сечение бойков цилиндрической части поверхности бойка), имеем для удельного давления протяжки следующее выражение

(1.37)

Формулы (1.32) и (1.37) являются расчетными для определения удельного давления протяжки под плоскими и вырезными бойками, а следовательно, и для определения необходимого пресса.