Lektsii / МСС / ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ

ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ

Основные определения. Тензор напряжения.

В однородном поле напряжение – это сила, которая приходится на единицу площади некоторого сечения, мысленно выделенного в теле. Причем эта сила показывает как действует отброшенная часть тела на оставшуюся.

На рисунке показана оставшаяся часть тела и вектор силы , которая действует от отброшенной части тела на элемент поверхности сечения , внешняя единичная нормаль к которому . Тогда более точно напряжение, действующее в точке М сечения запишется так

Рассмотрим в некоторой точке деформируемого тела бесконечно малый тетраэдр. По каждой грани выделенного из тела тетраэдра действуют свои векторы напряжений .

Подстрочные индексы показывают, как направлена нормаль к площадке, на которой они действуют ( напряжение действует по площадке, нормаль к которой параллельна оси Х и т.д. ) . Напряжение на наклонной площадке .

Каждый из указанных векторов напряжений можно задать его проекциями на координатные оси

Здесь второй индекс у указывает координатную ось на которую проецируется напряжение . Величины _xy , _xz , _yx , _yz , _zx , _zy - компоненты векторов напряжений, лежащие в плоскостях граней тетраэдра соответственно ВОС, АОС, АОВ – называются касательными напряжениями. Величины _xx , _yy , _zz – являются компонентами напряжений , перпендикулярными к граням тетраэдра и называются нормальными напряжениями.

Если заданы компоненты напряжений по трем взаимно перпендикулярным площадкам, проходящим через данную точку деформируемого тела, то напряжения на любой площадке, наклонной к координатным плоскостям можно подсчитать по формулам.

(1.1)

Здесь n_x , n_y , n_z – направляющие косинусы наклонной площадки по отношению к координатным плоскостям.

Коэффициенты (напряжения) при направляющих косинусах n_i в уравнениях (1.1.) образуют так называемый тензор напряжения

(1.2)

содержащий шесть существенных компонент, т.к. является симметричным ( _ij = _ji , т.е. _xy = _yx и т.д. ) .

Главные нормальные напряжения

Инварианты тензора напряжения

Площадки, на которых отсутствуют касательные напряжения, называются площадками главных нормальных напряжений ₁₁ , ₂₂ , ₃₃ . Индексы при последних назначаются по правилу

т.е. индекс "1" присваивается большему, а "3" – меньшему из значений.

Тензор напряжений, записанный в ортогональной системе координат, совпадающей с направлениями главных напряжений, имеет вид

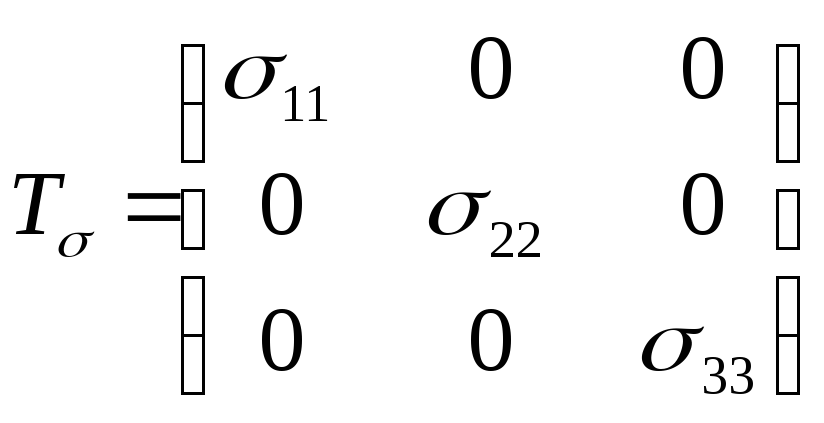(1.3)

Это означает, что напряженное состояние в любой точке деформируемого тела вызвано чистым растяжением или сжатием по трем взаимно перпендикулярным главным направлениям.

Главные напряжения являются корнями кубического уравнения

(1.4)

Коэффициенты , , этого уравнения называются инвариантами тензора напряжений. В произвольной ортогональной системе координат и ортогональной системе координат, совпадающей с направлениями главных нормальных напряжений они имеют вид

(1.5)

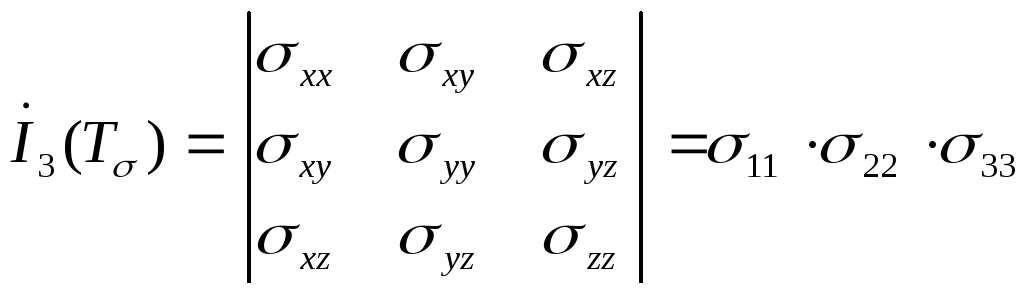
Величина, составленная из первого инварианта

(1.6)

называется средним ( или гидростатическим ) давлением в точке и имеет большое значение в теории пластичности и теории ОМД. В тензорной форме она записывается так :

Девиатор тензора напряжения и его инварианты

Так как материалы обладают, как правило, различными механическими свойствами по отношению к сдвигу и равномерному всестороннему сжатию, целесообразно представить тензор напряжения в виде суммы двух тензоров

(1.7)

Здесь   Е – так называемый шаровой тензор, соответствующий среднему давлению в некоторой точке деформируемого тела и отвечающий за изменение его объема.

, ( Е - единичный тензор )

а – тензор, характеризующий касательные напряжения в той же точке, называется девиатором напряжения и отвечает за изменение формы. Он характеризует насколько заданное напряженное состояние отличается от всестороннего равного растяжения или сжатия с главными напряжениями равными  .

Главные направления девиатора напряжения и тензора напряжения Т_ совпадают, а главные значения S₁₁ , S₂₂ , S₃₃ отличаются от ₁₁ , б₂₂, ₃₃ на величину среднего давления  .

Компоненты девиатора будем обозначать через S_ij . Тогда компоненты тензора Т_ можно представить через компоненты девиатора и шарового тензора   Е так :

(1.8)

Инварианты девиатора напряжения имеют вид:

(1.9)

Большую роль в теории пластичности играет второй инвариант. Неотрицательную величину

(1.10)

называют интенсивностью касательных напряжений. В главных напряжениях она имеет вид

(1.11)

В тензорной форме она запишется так

(1.12)

Интенсивность касательных напряжений обращается в нуль, когда напряженное состояние является состоянием гидростатического давления

Для чистого сдвига

; ;

Здесь  – напряжение чистого сдвига. Следовательно

В случае одноосного растяжения ( сжатия ) в направлении, например, оси Х

; ;

Тогда

(1.13)

Дифференциальные уравнения движения

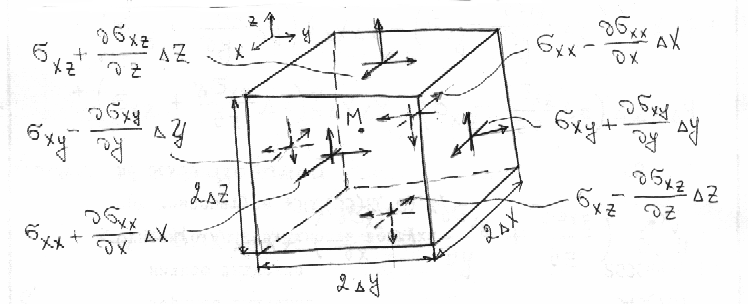
Рассмотрим окрестность точки М деформируемого тела, имеющего форму параллелепипеда с гранями, параллельными координатным плоскостям и центром в точке М . Длины ребер равны 2x , 2y , 2z .

Пусть _ij – напряжения в точке М , действующие по плоскостям, проходящим через эту точку и параллельным граням параллелепипеда. На гранях параллелепипеда напряжения будут несколько отличаться от _ij . На рисунке обозначены только те компоненты напряжений, действующих по граням, которые параллельны оси Х .

Определим составляющую _Х равнодействующей силы от напряжений на гранях элементарного параллелепипеда. Одинаковые напряжения на противоположных гранях отличаются на некоторое приращение.

После преобразований

Если сила, действующая на единицу массы элементарного параллелепипеда , скорость его движения , а ускорение , то уравнения движения параллелепипеда запишутся так :

Здесь V – объем параллелепипеда,  - плотность.

После преобразований получим

(1.14)

Уравнения (1.14) называются дифференциальными уравнениями движения. В тензорной форме они имеют вид

(1.15)

В частном случае, который чаще всего встречается в задачах теории ОМД, если отсутствуют массовые силы , а движение частиц достаточно медленное ( w_i  0 ) , уравнения (1.15) упрощаются

(1.16)

или в развернутом виде

(1.17)

и называются уже дифференциальными уравнениями равновесия.

Дифференциальные уравнения движения (1.14) и даже дифференциальные уравнения равновесия (1.16) не образуют замкнутой системы уравнений, так как три уравнения (1.14) содержат при заданных массовых силах девять неизвестных ( _ij и v_i ), а в случае медленных течений в уравнения (1.17) входит шесть искомых компонентов тензора напряжения.

Примечание.

Наличие запятой в подстрочных индексах соотношений (1.15) и (1.16) означает дифференцирование по соответствующей координате (индексу).