Lektsii / МСС / Теория деформированного состояния

Теория деформированного состояния.

В общем случае движение твердого недеформируемого тела можно представить суммой поступательного и вращательного движений. Если же тело ещё и деформируется, то движение будет более сложным. Из него можно выделить поступательное и вращательное движения, считая их переносными, а остальное – относительное движение – будет обусловлено только деформацией тела.

Тензор скорости деформации.

Пусть деформируемое тело в некоторый момент имело объем V и было ограничено поверхностью S . Внутри тела имеет место движение частиц. Это движение представлено векторным полем скорости .

Рассмотрим точку М деформируемого тела вместе с её окрестностью. Положение точки М в трехмерном пространстве задается радиусом вектором , компоненты (проекции) которого х, у, z.. Бесконечно малая окрестность окружает точку М . Положение произвольной точки М₁ в этой окрестности задается дополнительным вектором , с компонентами х , у , z .

Пусть точка М как точка деформируемого тела имеет в данный момент скорость движения с компонентами вдоль осей координат v_x , v_y, v_z . Скорость точки М₁ из области, окружающей точку М , будет отличаться от скорости точки М на величину , компоненты которой определяются соотношениями

(2. 1)

Коэффициенты при компонентах вектора в уравнениях (2.1) образуют так называемый тензор абсолютной производной векторного поля

(2.2)

Этот тензор может быть представлены в виде суммы

(2.3)

Здесь - тензор вращения с компонентами ( элементами матрицы )

, (2.4)

а - тензор скорости деформации с компонентами ( элементами матрицы )

(2.5)

Таким образом движение окрестности точки М сплошной среды состоит из: чистой деформации, определяемой тензором скорости деформации с компонентами (2.5); вращения области относительно точки М , определяемого тензором вращения с компонентами (2.4) и поступательного движения, определяемого вектором скорости точки М.

Компоненты тензора скорости деформации в развернутой форме имеет вид

(2.6)

(2.7)

и называются: (2.6) – скоростями удлинения в направлении осей соответственно Х,У,Z, а удвоенные (2.7) – скоростями сдвига в плоскостях соответственно ХОУ, УОZ, ZОХ.

Уравнения (2.6) и (2.7) называются геометрическими или кинематическими соотношениями связи скоростей течения и компонентов тензора скорости деформации.

Тензор скорости деформации имеет вид

(2.8)

Главные скорости удлинения.

Инварианты тензора скорости деформации.

Тензор скорости деформации имеет взаимно перпендикулярные главные направления с соответствующими главными скоростями удлинения по ним , , . Индексация главных скоростей удлинения принята такой

.

При этом деформацию в любой точке тела можно представить удлинением или укорочением по трем взаимно перпендикулярным главным направлениям некоторого элементарного параллелепипеда.

Инварианты тензора скорости деформации запишутся

(2.9)

Особое значение в прикладной теории пластичности играет первый инвариант, определяющий скорость относительного изменения объема тела

=++

Девиатор тензора скорости деформации и его инварианты.

Уравнение неразрывности.

Выделим из тензора скорости деформации новый тензор, который связан только с изменением формы и называется девиатором скорости деформации

(2.10)

где Е – единичный тензор.

Компоненты определяются соотношениями

(2.11)

или более подробно

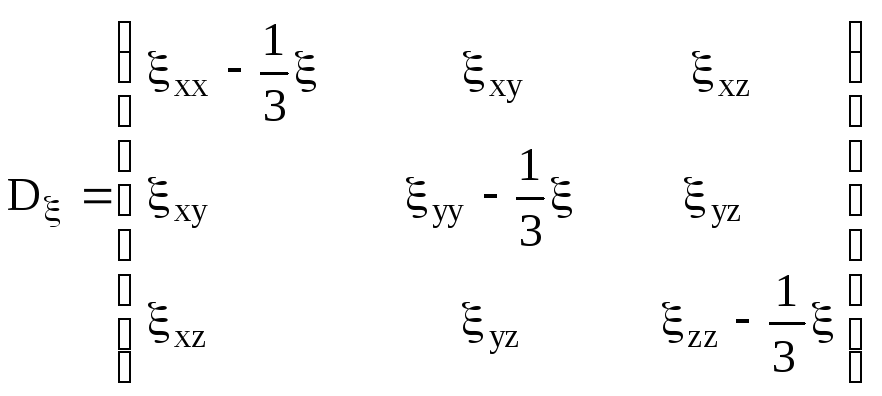(2.12)

Тензор - называется шаровым и соответствует только изменению объема.

Главные направления девиатора скорости деформации и тензора скорости деформации совпадают. Это следует из соотношения (2.10), так как для единичного тензора Е главным направлением будет любое направление.

Если материал несжимаем ( довольно распространенная гипотеза ), то

=0 и =

то есть в этом случае компоненты девиатора и тензора скорости деформации совпадают

,

а соотношение

=++ = 0 или =++=0 (2.13)

представляет собой условие несжимаемости.

Инварианты девиатора скорости деформации имеют вид

Большую роль в теории пластичности играет второй инвариант, неотрицательную величину, составленную из которого

.(2.15)

называют интенсивностью скоростей деформации сдвига. В тензорной форме для несжимаемого материала она запишется так

(2.16)

Интенсивность скоростей деформации сдвига обращается в нуль, если материал равномерно расширяется или сжимается, когда

==.

Для чистого сдвига, когда =0, кроме, например 0

Для одноосного растяжения или сжатия несжимаемого материала, когда 0,

Уравнение неразрывности определяет монотонность процесса деформации и отсутствие нарушения сплошности ( разрывов и т.п. ) в деформируемом теле.

Данное уравнение выводится как следствие закона сохранения массы тела в процессе деформации

(2.17)

Здесь - массовая плотность; - объем малой окрестности, окружающей точку М; - её масса. Скорость частицы в точке М - .

Исходя из отмеченных условий процесса деформации функции и предполагаются непрерывными и достаточное число раз дифференцируемыми функциями своих аргументов.

Уравнение неразрывности имеет вид

(2.18)

В частном случае несжимаемого материала (=const) оно переходит в следующее уравнение

(2.19)

или, что то же самое

++=0

и представляет собой условие несжимаемости (отмеченное ранее).

Уравнение непрерывности и рассмотренные ранее дифференциальное уравнения движения еще не образуют замкнутой системы уравнений, так как четыре уравнения содержат десять неизвестных ( шесть компонентов тензора напряжений , плотность и три компоненты вектора скорости v_i ).

Несколько позднее эта система будет замкнута путем введения шести физических уравнений , которые не содержат дополнительных неизвестных, а объединяют напряжения и скорости движения.

Теория течения в приращениях и перемещениях.

В случае, когда механические свойства металлов зависят не от скорости деформации, а от величины самой деформации, то кинематические уравнения теории деформированного состояния целесообразно составить в приращениях перемещений.

Рассмотрим некоторый момент времени t . Введем как параметр бесконечно малый и достаточный, для того чтобы теория была точной, промежуток времени dt . За этот отрезок времени частица материала в произвольной точке деформируемого тела получила приращение перемещения

Если повторить все выкладки, выполненные ранее, но для приращения перемещений, то можно показать, что деформированное состояние в окрестности точки будет характеризоваться симметричным тензором бесконечно малого приращения деформации

, (2.20)

где

(2.21)

Кроме того, частицы окрестности произвольной точки получат поступательное смещение на величину и поворот, тензор которого имеет компоненты

(2.22)

Тензор , записанный относительно главных приращений деформаций имеет вид

(2.23)

Правило присвоения индексов главным приращениям деформаций остаётся прежним

.

Тензор приращения деформаций имеет три инварианта, значения которых легко получить из инвариантов тензора заменой соответствующих компонентов .

Первый инвариант выражает изменение приращения объема

(2.24)

Девиатор приращения деформации определен так

(2.25)

Его компоненты равны

(2.26)

Девиатор приращения деформации имеет свои инварианты. Так второй инвариант имеет вид

(2.17)

Важное значение имеет интенсивность приращения степени деформации сдвига

(2.28)

Если материал несжимаем и =0 , то справедлива формула

(2.29)

Как видно из изложенного, между теорией деформированного состояния в скоростях течения и в приращениях перемещений имеет место полная аналогия. Следуя этому, всегда можно дополнить рассмотренную теорию недостающими уравнениями.

Рассмотрим, далее, бесконечно малый промежуток времени dt . Величина dt играет роль параметра

(2.30)

Следовательно, из формулы (2.29) вытекает

, (2.31)

где =0.

При движении частицы в поле тензора будет накапливаться деформация. Величина определяемая формулой

, (2.32)

в которой интегрирование производится вдоль траектории движения частицы, называется степенью деформации сдвига.

9