
ОТЦ_заочники_2014 / ОТЦ л_р_5_6_7_8
.pdf
4. Обработка результатов |
|
4.1. По результатам измерений рассчитайте АЧХ KU ( f ) Um2 |
Um1 |
и ФЧХ в градусах U(f) = 360 f tз или в радианах U(f) = 2 |
f tз |
исследуемых цепей, результаты занесите в таблицы (см. п. 3.1.6).
4.2.Постройте графики АЧХ и ФЧХ исследуемых цепей.
4.3.По экспериментальным графикам АЧХ определите частоты среза, составьте таблицу сравнения результатов расчета и эксперимента.
fср, кГц |
RC |
CR |
RL |
LR |
|
RLC |
|
|
2Rкр |
Rкр |
0,5Rкр |
||||||
|
|
|
|
|
||||
Расч. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Эксп. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4.4. Сформулируйте выводы по проделанной работе.
5. Контрольные вопросы
1.Что такое комплексная частотная характеристика цепи? Какие существуют виды КЧХ? Как определяется размерность КЧХ?
2.Что такое амплитудно-частотная характеристика? Какой ее физический смысл?
3.Что такое фазо-частотная характеристика? Какой ее физический смысл?
4.Какими свойствами обладают КЧХ линейных цепей? Как рассчитать КЧХ цепи?
5.Как определить реакцию цепи на заданное гармоническое воздействие, если известна КЧХ?
6.Что такое частота среза?
7.Какой вид имеют КЧХ цепей, состоящих только из сопротивлений?
8.Какой вид имеют КЧХ цепей, содержащих один реактивный элемент (емкость или индуктивность)?
9.Какой вид имеют КЧХ цепей, содержащих различные реактивные элементы (емкость и индуктивность)?
10.От чего зависит вид КЧХ последовательной RLC-цепи и каким образом?
11
Лабораторная работа № 6
РЕЗОНАНСНЫЕ ЯВЛЕНИЯ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Цель работы
Практическое знакомство с частотными характеристиками резонансных цепей. Экспериментальная проверка правильности соотношений, описывающих характеристики простого и сложного колебательных контуров.
1.Основные теоретические положения
Втеории цепей используют следующее определение резонанса. Резонансом называют такой режим работы электрической цепи, содержащей емкости и индуктивности, при котором ее комплексное входное сопротивление (или проводимость) имеет чисто резистивный характер и, следовательно, ток и напряжение на входе совпадают по фазе.
Последовательный колебательный контур
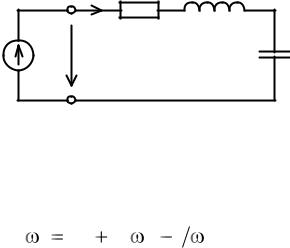
Простейшей электрической цепью, в которой наблюдается резонанс, является последовательный колебательный контур, состоящий из катушки индуктивности и конденсатора, подключенных последовательно к источнику энергии (рис. 6.1). Сопротивление Rп учитывает потери энергии в контуре.
|
i(t) |
Rп |
L |
e(t) |
u(t) |
|
C |
Рис. 6.1. Эквивалентная схема последовательного колебательного контура
Комплексное входное сопротивление последовательного контура
Z( j ) Rп j( L 1 C) , |
(6.1) |
откуда следует, что резонансная частота
12
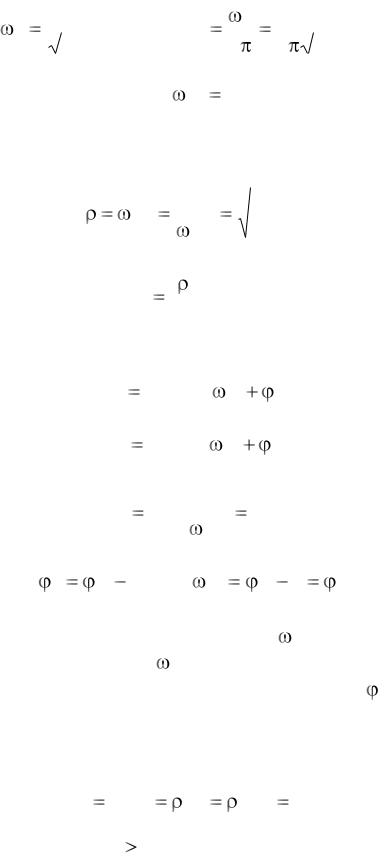
|
|
1 |
|
или |
f0 |
|
0 |
1 |
|
, |
(6.2) |
||
0 |
|
|
|
|
|
|
|
|
|||||
|
|
|
2 |
|
|
|
|
|
|||||
|
LC |
|
|
|
2 LC |
||||||||
|
|
|
|
|
|
|
|
|
|
||||
при этом
Z ( j 0 ) Rп .
Кроме резонансной частоты основными параметрами контура являются характеристическое сопротивление, равное полному сопротивлению индуктивности или емкости при резонансе,
|
|
0L |
|
1 |
|
|
|
|
|
L |
|
, |
|
(6.3) |
||
|
|
|
0C |
|
|
|
C |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||
и добротность |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Q |
|
. |
|
|
|
|
|
|
|
|
|
(6.4) |
||
|
|
Rп |
|
|
|
|
|
|
|
|
|
|||||
Если к контуру приложить напряжение с частотой, равной |
||||||||||||||||
резонансной |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u(t) |
Um cos( |
0t |
|
|
|
U ) , |
|
||||||||
то в контуре будет протекать ток |
|
|
|
|
|
|
|
|
|
|
||||||
|
i(t) |
Im cos( |
0t |
|
|
|
I ) . |
|
||||||||
При этом амплитуда тока |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Im |
|
|
Um |
|
|
|
|
Um |
, |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
| Z ( j |
0 ) | |
|
Rп |
|
|||||||||||
|
|
|
|
|
||||||||||||
а начальная фаза |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I |
U |
arg Z ( j |
0 ) |
|
|
|
U |
|
0 |
U . |
||||||
Любое отклонение частоты от резонансной приведет к появлению реактивной составляющей Z(j ), увеличению полного сопротивления контура |Z(j )|, следовательно, к уменьшению амплитуды тока Im и отклонению начальной фазы I от начальной фазы приложенного напряжения.
Амплитуды напряжений на реактивных элементах при резонансе
UmL UmC Im |
Um |
QUm . |
|
Rп |
|||
|
|
Поскольку добротность Q 1, то в последовательном контуре имеет место увеличение амплитуд напряжений на индуктивности и емкости, поэтому такой резонанс называется резонансом напряжений.
13

Параллельный колебательный контур
Другим примером электрической цепи, в которой имеют место резонансные явления, служит параллельный колебательный контур. В этом случае катушка индуктивности и конденсатор подключаются параллельно источнику. На практике обычно рассматривают эквивалентную схему, показанную на рис. 6.2, при этом все потери энергии в контуре относят к индуктивной ветви и учитывают в виде
сопротивления RL ( Rп |
RL ). |
|
|
|
||||||
|
|
|
|
i(t) |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
iL(t) |
|
iC(t) |
|
|
|
|
|
|
|
|
|
|||
j(t) |
|
|
|
u(t) |
|
|
RL |
|
|
C |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
L |
|
|
||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 6.2. Эквивалентная схема параллельного колебательного контура
Комплексное входное сопротивление параллельного контура
|
|
|
|
Z ( j |
) |
|
(RL |
j |
L)(1 |
j C) |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
(6.5) |
||||
|
|
|
|
|
RL |
j( |
L |
1 |
|
C) |
||||||||||
Если рассматривать контур на относительно высоких частотах, |
||||||||||||||||||||
считая |
L |
RL , то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
( j L)(1 |
j |
C) |
|
|
|
|
L C |
|
|
|
|
2 |
|
|
||||
Z ( j ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
, (6.6) |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
RL |
j( L |
1 |
C) |
|
RL |
j( |
L |
1 |
C) |
|
|
RL j( L 1 |
C) |
||||||
где |
характеристическое сопротивление (6.3), и на резонансной |
|||||||||||||||||||
частоте |
р |
0 , см. формулу (6.2), |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
||
|
|
|
Z ( j |
р ) |
|
Z ( j |
0 ) |
Roe |
|
|
|
|
|
Q , |
(6.7) |
|||||
|
|
|
|
|
RL |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Q |
|
RL |
добротность. Величина Roe |
называется резонансным |
||||||||||||||||
сопротивлением контура. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Если к контуру подвести ток с частотой, равной резонансной, |
||||||||||||||||||||
|
|
|
|
|
i(t) |
|
Im cos( рt |
|
I ) , |
|
|
|||||||||
то напряжение на контуре будет изменяться по закону
14
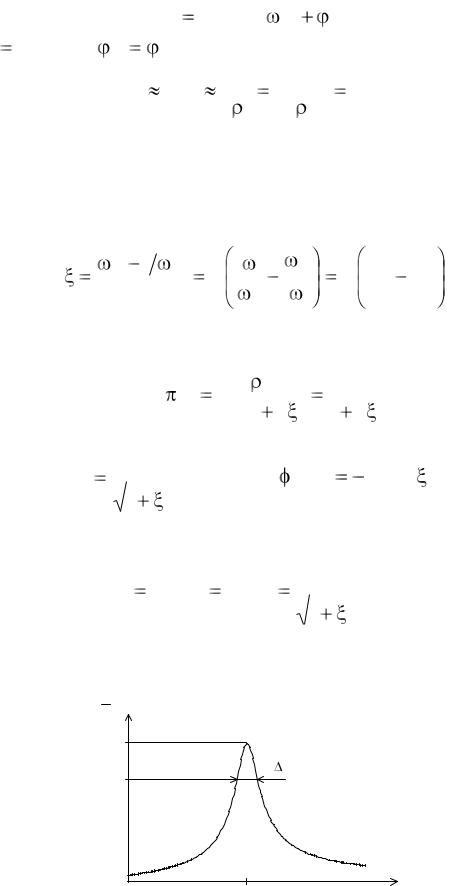
|
u(t) Um cos( |
рt U ), |
|||
где Um RoeIm , а U |
I . Амплитуды токов в ветвях контура |
||||
|
Um |
RoeIm |
QIm . |
||
ImL |
ImC |
|
|
|
|
|
|
||||
Таким образом, в параллельном колебательном контуре имеет место увеличение амплитуд токов в индуктивности и емкости на резонансной частоте в Q раз или резонанс токов.
Для описания частотных характеристик колебательных контуров (6.1), (6.6) вводится определение обобщенной расстройки
L 1 |
C |
Q |
|
|
р |
Q |
f |
|
fр |
. |
(6.8) |
RL |
|
р |
|
|
fр |
|
f |
||||
|
|
|
|
|
|
|
|
И тогда зависимость комплексного входного сопротивления контура от частоты (6.6) описывается выражением:
|
|
2 |
|
|
Roe |
|
|
Z ( j2 f ) |
|
|
|
|
. |
(6.9) |
|
|
|
|
|
||||
|
RL (1 |
|
j ) 1 j |
|
|||
АЧХ и ФЧХ соответственно будут равны:
Z ( f ) |
|
|
Roe |
и |
z ( f ) |
|
|
arctg( ) . |
(6.10) |
||||||||
|
|
|
|
|
|
|
|
||||||||||
1 |
2 |
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Для сравнения колебательных контуров с различными |
|||||||||||||||||
параметрами удобнее пользоваться нормированными АЧХ |
|
||||||||||||||||
|
|
|
|
|
|
Z ( f ) |
|
Z ( f ) |
1 |
|
|
. |
(6.11) |
||||
Z ( f ) |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Z ( fр ) |
|
Roe |
1 |
2 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||
На рис. 6.3 показана нормированная АЧХ параллельного колебательного контура.
Z(f) |
|
1 |
|
|
2 f |
0,707 |
|
0 |
f |
fр |
|
Рис. 6.3. Нормированная АЧХ параллельного |
|
|
колебательного контура |
15
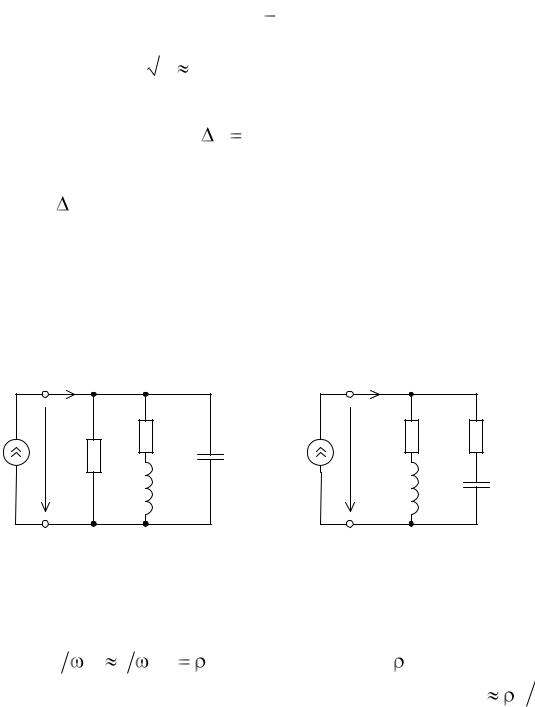
Полное сопротивление контура, т.е. АЧХ, существенно зависит от частоты. Если подать на такой контур сумму гармонических токов с различными частотами и одинаковыми амплитудами, то на контуре выделятся токи с частотами, лежащими в окрестности резонансной частоты fр, поскольку сопротивление контура для них будет велико и близко к Roe. Для токов с частотами, далеко отстоящих от fр, сопротивление контура будет мало, и они пройдут через контур со значительным ослаблением. Такое свойство электрических цепей – выделять одни сигналы среди других называется избирательностью.
Диапазон частот, на границах которого полное сопротивление
|
|
|
|
|
|
контура изменяется в 2 0,707 |
раз от максимального |
значения, |
|||
называется полосой пропускания |
|
|
|
||
|
|
2 f |
fр |
. |
(6.12) |
|
|
Q |
|||
|
|
|
|
|
|
Отсюда видно, что чем выше добротность Q, тем меньше полоса пропускания 2 f и тем лучше избирательные свойства контура.
Врадиотехнических устройствах колебательный контур входит
всостав более сложных цепей, при этом параллельно с ним
включается некоторое сопротивление нагрузки Rн (рис. 6.4), которым может быть, например, выходное сопротивление источника или входное сопротивление следующего каскада.
|
i(t) |
|
|
i(t) |
|
|
RL |
|
|
RL |
R’н |
j(t) |
u(t) Rн |
C |
j(t) |
u(t) |
|
|
L |
|
|
L |
C |
Рис. 6.4. Эквивалентная схема параллельного контура, зашунтированного сопротивлением Rн
В этом случае, преобразуя параллельное соединение элементов Rн и C в последовательное, рассматривая диапазон частот, близких к
резонансной (1 С 1 0С |
), и допуская Rн >> , получаем, что в |
||
контур вносится дополнительное сопротивление потерь |
R' |
2 R . |
|
|
|
н |
н |
В таком случае эквивалентная добротность получается равной
16
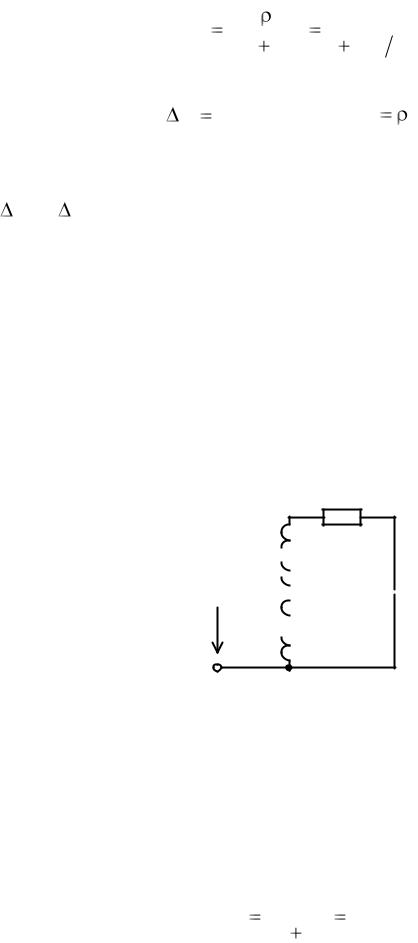
Qэ |
|
|
|
Q |
. |
(6.13) |
|
|
|
|
|
||||
RL |
R'н |
1 Roe Rн |
|||||
|
|
|
|||||
Остальные параметры также меняются на эквивалентные:
2 f |
|
fр |
, |
R |
Q . |
(6.14) |
э |
|
|||||
|
Qэ |
|
oeэ |
э |
|
|
|
|
|
|
|
|
|
Таким образом, сопротивление Rн |
приводит |
к снижению |
||||
добротности контура (Qэ < Q) |
и расширению полосы пропускания |
|||||
(2 fэ > 2 f), т.е. к ухудшению его избирательных свойств.
Сложный колебательный контур
Сложный колебательный контур или контур с частичным включением реактивного элемента позволяет уменьшить влияние Rн на избирательные свойства за счет меньшего резонансного сопротивления Roe. Кроме того, такой контур обладает свойством трансформации сопротивлений, что позволяет использовать его для согласования источника с нагрузкой. На рис. 6.5 показана эквивалентная схема колебательного контура с частичным включением индуктивности.
RL
L1 i(t)
i(t) 



 C u(t) L2
C u(t) L2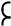
Рис. 6.5. Эквивалентная схема контура с частичным включением индуктивности
Частичное включение реактивного элемента учитывается с помощью коэффициента включения p, который равен отношению амплитуды напряжения на зажимах, которыми контур включается во внешнюю цепь, к амплитуде напряжения на всем контуре. В случае частичного включения индуктивности, если L1 и L2 являются отдельными катушками (рис. 6.5), коэффициент включения
p |
|
L2 |
|
L2 |
, |
(6.15) |
|
L1 |
L2 |
L |
|||||
|
|
|
|
17

где L L1 L2 общая индуктивность контура.
Основным резонансом в сложном контуре является резонанс токов, частота которого
|
|
1 |
1 |
|
. |
(6.16) |
|||
|
|
|
|
|
|
|
|
||
р 0т |
|
|
|
|
|
|
|||
LC |
|
|
|
(L1 L2 )C |
|||||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
В окрестности частоты резонанса токов сложный контур ведет себя аналогично простому параллельному колебательному контуру, но его резонансное сопротивление
R p2 |
Q. |
(6.17) |
oe |
|
|
Поскольку коэффициент включения p принимает значения от 0 до 1, Roe сложного контура будет меньше Roe простого параллельного контура в p2 раз.
Как правило, на практике частичное включение индуктивности реализуется путем выполнения отвода от катушки колебательного контура, в этом случае формула для коэффициента включения усложняется (см. расчетную часть), а простой и сложный контура имеют одинаковые резонансную частоту р (fр), характеристическое сопротивление , добротность Q и отличаются только резонансным сопротивлением Roe и эквивалентными параметрами Qэ, 2 fэ, Roeэ.
Особенностью частотной характеристики (рис. 6.6) сложного контура является резонанс напряжений в последовательной ветви L1C
(см. рис. 6.5), частота которого 0н 1 
 L1C . В окрестности этой
L1C . В окрестности этой
частоты сложный контур ведет себя аналогично последовательному колебательному контуру.
Z(f) |
|
|
|
Roe |
|
|
|
RL |
|
|
|
0 |
|
f |
|
f0т |
f0н |
||
|
|||
Рис. 6.6. АЧХ сложного колебательного контура |
|||
с частичным включением индуктивности |
|||
18
2. Расчетная часть
Данные для расчетов (резонансная частота fр, индуктивности L1, L1 , L1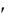 , сопротивление потерь RL1 и величины сопротивлений Ri, Rш) находятся в таблице в лаборатории.
, сопротивление потерь RL1 и величины сопротивлений Ri, Rш) находятся в таблице в лаборатории.
2.1.Для простого параллельного незашунтированного колебательного контура (рис. 6.7) рассчитайте:
 характеристическое сопротивление ;
характеристическое сопротивление ;
 добротность Q;
добротность Q;
 резонансное сопротивление Roe;
резонансное сопротивление Roe;  полосу пропускания 2 f.
полосу пропускания 2 f.
2.2.Определите Qэ, Roeэ, 2 fэ для случаев, когда контур зашунтирован:
 сопротивлением источника тока Ri;
сопротивлением источника тока Ri;
 одновременно сопротивлением источника тока Ri и шунтом
одновременно сопротивлением источника тока Ri и шунтом
Rш.
Uвх SUвх |
Ri |
Rш |
RL1 |
L1' |
|
C1 |
L1 |
||||
|
|
|
|||
|
|
|
|
L1" |
Рис. 6.7. Эквивалентная схема измерительной установки
2.3.Рассчитайте нормированную зависимость модуля входного сопротивления простого параллельного колебательного контура
Z ( f ) от частоты f (АЧХ) см. формулы (6.8), (6.11), для случаев, когда контур зашунтирован:
 сопротивлением Ri;
сопротивлением Ri;
 одновременно сопротивлениями Ri и Rш. Постройте графики нормированных АЧХ Z ( f ) .
одновременно сопротивлениями Ri и Rш. Постройте графики нормированных АЧХ Z ( f ) .
Расчет и построение графиков нормированных АЧХ проведите в интервале частот от fмин до fмакс, которые находятся из условия:
Z ( fмин ) Z ( fмакс ) 0,2Z ( fр ) .
Графики постройте на одном рисунке.
2.4.Повторите пп. 2.1 2.3 для сложного контура с двумя индуктивностями L1 и L1 (рис. 6.7). При расчете коэффициента
(рис. 6.7). При расчете коэффициента
19
включения p учтите, что L1 и L1
и L1 являются частями одной катушки L1 и поэтому между ними существует взаимная индуктивность M. Таким образом,
являются частями одной катушки L1 и поэтому между ними существует взаимная индуктивность M. Таким образом,
L1 |
L1' L1'' 2M , |
|||
p |
|
L1 |
'' M |
. |
|
|
L1 |
||
|
|
|
|
|
Расчет и построение АЧХ сложного контура произведите для частот вблизи частоты параллельного резонанса (резонанса токов) fр. Диапазон частот выбирается аналогично п. 2.3.
2.5.Изучите методику измерения АЧХ и порядок выполнения работы. Ответьте на контрольные вопросы.
3. Методика измерения АЧХ
3.1.Данная работа выполняется на блоке «Избирательные цепи» лабораторного стенда. Колебательный контур является нагрузкой резонансного усилителя. Если в цепи действуют только гармонические токи и напряжения, то усилительный элемент можно представить как источник тока, управляемый напряжением (см. рис. 6.7), ток которого
I SUвх ,
где S – крутизна вольт-амперной характеристики усилительного элемента; Uвх – входное напряжение усилителя.
Внутреннее сопротивление источника Ri равно выходному сопротивлению усилительного элемента.
Пользуясь эквивалентной схемой (см. рис. 6.7), напряжение на контуре можно записать следующим образом
Uк ( f ) IZ( f ) SUвх Z( f ), |
(6.18) |
где Z(f) – модуль входного сопротивления контура, зависящий от частоты входного воздействия f. При этом сопротивление Ri (или Ri и Rш), подключенное параллельно контуру, пересчитывается последовательно в контур (см. рис. 6.4), что приводит к уменьшению эквивалентной добротности и изменению эквивалентных параметров согласно формулам (6.13), (6.14).
На резонансной частоте
Uк ( fр ) SUвх Z ( fр ). |
(6.19) |
20
