Лабораторные работы по СВЧ / ЛР №4

Лабораторная работа № 4

ИССЛЕДОВАНИЕ ПОЛОСНОПРОПУСКАЮЩИХ ВОЛНОВОДНЫХ ФИЛЬТРОВ СВЧ

Цель работы: Освоение методики расчетов фильтров СВЧ. Исследование частотных характеристик полосковых полоснопропускающих фильтров с помощью авто­матической измерительной линии.

Продолжительность работы -2ч

Коллоквиум -2ч

Самостоятельная подготовка - 2 ч

Основные определения, методы расчёта фильтров СВЧ

Фильтрами СВЧ называют пассивные четырехполюсники с резко выраженной частотной избирательностью. Они находят широкое приме­нение в радиотехнических системах для частотной селекции сигналов, подавления помех. Наиболее широкое распространение в диапазоне частот от 1 до 20ГГц получили фильтры, выполненные на основе полосковых линий. Подробное описание методики расчета фильтров СВЧ находится в [1].

Расчетное задание: по приведенным ниже техническим данным рассчитать геометрические размеры полосковых фильтров 2-го и 4-го порядков с четвертьволновыми связями. Колебательные контуры фильтра реализовать в виде двух шлейфов холостого хода.

Номер бригады	1	2	3	4	5	6	7	8
Центральная частота f0, МГц	900	900	950	950	1000	1000	1050	1050
Полоса пропускания по уровню -3дБ Δf, МГц	100	150	100	150	100	150	100	150

допустимый уровень вносимого фильтром затухания в полосе пропускания В_ф1=3дБ,

эффективная относительная диэлектрическая проницаемость подложки ε_эфф=1,4,

ширина полоски с волновым сопротивлением 50Ом W_50Ом=11мм.

Порядок расчета:

1. Расчет АЧХ идеального фильтра:

В этом пункте выполняется расчет АЧХ идеального фильтра Баттерворта заданного порядка.

1.1. Расчет верхней и нижней частот диапазона.

f_в=f₀+Δf/2, f_н=f₀-Δf/2.

1.2. Расчет и построение идеальной АЧХ фильтра.

Вносимое фильтром затухание [дБ], где

,

– нормированная частота для полосно-пропускающего фильтра,

n – порядок фильтра.

При построении идеальной АЧХ необходимо помнить, что модуль коэффициента передачи равен -В_ф [дБ]. АЧХ необходимо строить в диапазоне частот от f₀-3Δf до f₀+3Δf. Также при использовании пакетов математического моделирования необходимо помнить, что нормированная частота является функцией частоты.

2. Расчет элементов фильтра на линиях передачи с четвертьволновыми связями:

2.1. Расчет g-параметров фильтра-прототипа

2.2. Расчет нагруженной добротности контуров эквивалентной схемы

.

2.3. Определение по графикам длин шлейфов при реализации колебательных контуров на линиях передачи [2]

Топология контуров фильтра в виде двух шлейфов ХХ и КЗ(рис.А) и в виде двух ХХ шлейфов(рис.Б)

Для ХХ и КЗ шлейфов Для ХХ шлейфов

Необходимо помнить, что при реализации контура в виде двух шлейфов ХХ и КЗ , а при реализации контура в виде двух ХХ шлейфов , где

– длина волны в линии,

– длина волны в свободном пространстве.

Частоту при расчете длин отрезков необходимо принять равной центральной частоте f₀. В дальнейших расчетах частота – переменная. Определить l₁ и l₂ по графику.

Ниже на рисунке изображена топология фильтра второго порядка.

Ниже на рисунке изображена топология фильтра четвертого порядка.

3. Расчет АЧХ фильтра на линиях

В этом пункте производится расчет АЧХ фильтра с учетом того, что частотная зависимость реактивного сопротивления шлейфов носит тангенциальный характер, в отличие от линейного характера такой зависимости для элементов с сосредоточенными параметрами.

3.1. Расчет эквивалентной нормированной входной проводимости контура.

Проводимость контура складывается из двух входных проводимостей реактивных шлейфов (ХХ и КЗ или ХХ и ХХ):

, , где

– коэффициент фазы линии,

l – длина соответствующего шлейфа.

Соответственно входная нормированная проводимость контура рассчитывается как сумма проводимостей двух шлейфов или .

3.2. Расчет характеристической матрицы А фильтра (классическая матрица передачи).

Матрица А фильтра рассчитывается как произведение матриц А его составляющих. То есть для фильтра с четвертьволновыми связями:

, где А₁, А₃, А₅ и т.д. – матрицы А параллельных колебательных контуров; А₂, А₄, А₆ и т.д. – матрицы А четвертьволновых отрезков линии передачи, связывающих контуры.

Для отрезка линии передачи без потерь длиной l .

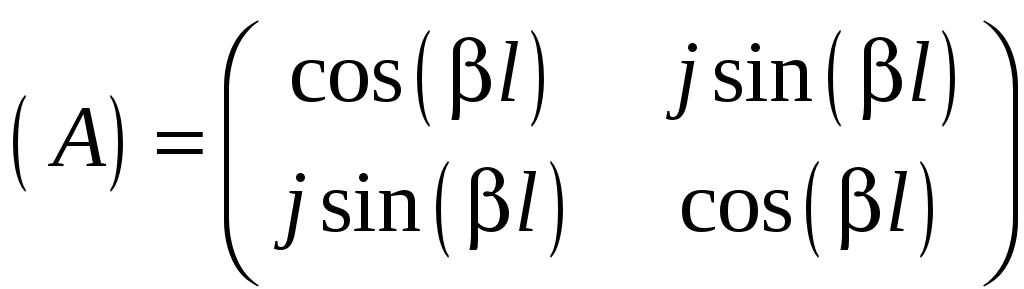Для параллельно включенной нормированной проводимости .

3.3. Расчет модуля коэффициента передачи фильтра на микрополосковых линиях.

Необходимо найти коэффициент S₂₁ или S₁₂ (фильтр - реактивный взаимный четырехполюсник):

.

Для пересчета в дБ следует пользоваться формулой.

.

Файл для расчета находится в папке.

3.4. Выполнить построение АЧХ фильтра на линиях передачи на том же графическом поле, которое используется в п.1.

При выполнении расчетов в пакете математического моделирования для построения АЧХ фильтра на линиях передачи по п. 3 необходимо помнить, что коэффициент фазы в линии является функцией частоты, а длины отрезков линий передачи частотно не зависимы.

Задание к экспериментальной части.

По результатам расчетов п. 2 реализовать топологию фильтров 2-го и 4-го порядков. Исследовать АЧХ фильтров. Определить полосу пропускания фильтров по уровню -3дБ и -15дб. На графические поля из п.1 нанести экспериментальные АЧХ фильтров.

Описание лабораторной установки

В лабораторной работе исследуются полоснопропускающие фильтры реализованные на полосковых линиях. Для снятия частотных характеристик коэффициента передачи используется панорамный измеритель Р4-11. Инструктаж по работе с прибором проводится преподавателем.

Элементы фильтров вырезаются из фольги и наклеиваются на рабочий стенд с полосковой линией передачи.

Содержание отчёта:

1. Цель работы.

2. Результаты расчетов фильтров.

3. Эскизы топологии исследуемых фильтров с указанием рассчитанных или заданных размеров шлейфов.

4. Схемы измерений.

5. Результаты измерений.

6. Выводы по проделанной работе.

Контрольные вопросы

1. Что такое низкочастотный прототип фильтра СВЧ?

2. Факторы, влияющие на уровень потерь в полосе пропускания для полоснопропускаюших фильтров СВЧ.

3. Чем определяется требуемое число резонаторов полоснопропускающего фильтра?

5. Особенности фильтров с четвертьволновыми связями.

8. Способы настройки полосковых резонаторов в фильтрах СВЧ.

9. Чем определяется собственная добротность полосковых резонато­ров и как она влияет на характеристики полоснопропускающих фильтров?

10. Методика измерения частотных характеристик фильтров с помощью панорамного измерителя Р4-11.

Литература:

1. Вольман, Пименов. Техническая электродинамика.

2. Фельдштейн А.Л.Явич Л.Р.Синтез четырехполюсников и восьмиполюсников на СВЧ.Изд.2-е,пер.и доп.1971.djvu стр.319