Лабораторная работа № 7 «Щелевые волноводные антенны»

Цель работы: Изучение принципа действия и конструкций щелевых волноводных антенн, выполненных на прямоугольном волноводе; исследование эквивалентных параметров щелей и диаграмм направленности многощелевых решёток.

Продолжительность работы – 2 часа. Коллоквиум – 2 часа. Домашняя подготовка – 2 часа.

1. Краткие сведения о щелевых волноводных антеннах

На стенках волновода протекают электрические токи, поверхностная плотность которых определяется соотношением

, (1)

где – вектор магнитного поля у стенки,

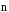– единичный вектор нормали.

Таким образом, плотность электрического тока численно равна напряжённости магнитного поля, а силовые линии тока и поля взаимно перпендикулярны. В прямоугольном волноводе с волной на широкой стенке имеются продольная и поперечная составляющая тока, а на узкой стенке – только поперечная – . Распределение этих составляющих по контуру поперечного сечения показано на рис. 1.

Рис. 1

Излучающая щель на стенке волновода располагается так, чтобы она пересекалась линиями поверхностных токов. Наиболее часто применяют поперечные и продольные щели на широкой стенке и наклонные щели на узкой стенке. Длина щелей берётся ~ , чтобы щели были резонансными, то есть представляли для волновода чисто активную нагрузку. При этом щели, возбуждаемые продольным током, имеют эквивалентную схему в виде последовательного сопротивления, а возбуждаемые поперечным током – параллельной проводимости (рис. 2).

Рис. 2

Формулы для безразмерных нормированных эквивалентных сопротивлений и проводимостей (отнесённых к волновому сопротивлению или проводимости волновода) имеют следующий вид:

1. Сопротивление поперечной щели

(2)

2. Проводимость продольной щели

(3)

3. Проводимость наклонной щели на узкой стенке при малых углах наклона

(4)

Диаграммы направленности (ДН) одиночной щели в плоском бесконечном экране можно определить, используя принцип двойственности. Хотя волновод является экраном ограниченных размеров сложной формы, однако, в плоскости, проходящей через ось волновода, где размеры экрана велики по сравнению с длиной волны, можно использовать приближённо следующие формулы:

1. Плоскость (для продольных щелей)

. (5)

2. Плоскость (для поперечных и наклонных щелей)

. (5а)

Угол в формуле (4) отсчитывается от нормали к экрану, а длина щели равна ~ .

Наклонные щели излучают поле с наклонной поляризацией, причем соотношение между вертикальной и горизонтальной составляющими вектора определяется углом наклона щелей (=0 – вертикальная щель, =90⁰ – горизонтальная щель).

.

Обычно

Для увеличения направленности в волноводе прорезают несколько щелей, образующих равномерную решётку. Различают два основных типа многощелевых волноводных антенн:

1. резонансные,

2. нерезонансные.

В резонансных антеннах все щели питаются синфазно. Для этого расстояния между поперечными щелями должны быть равны , что даёт сдвиг фаз питания на . Продольные щели на широкой стенке и наклонные на узкой располагаются на расстояниях , что даёт сдвиг фаз на . Дополнительный сдвиг фаз на , необходимый для синфазного питания, обеспечивается для продольных щелей противоположным смещением соседних щелей или возбуждающих их элементов от оси волновода, а для наклонных щелей – противоположным наклоном (см. рис. 5). С одного конца волновод резонансной антенны закорачивается поршнем так, что в волноводе устанавливается стоячая волна, а щели располагаются в пучностях продольной или поперечной составляющих поверхностного тока. Для этого расстояние между последней щелью и поршнем должно быть равно целому числу для поперечных щелей и нечётному числу для продольных и наклонных щелей. Для согласования резонансной антенны из щелей с питающим волноводом необходимо, чтобы эквивалентное сопротивление (проводимость ) каждой щели определялось из соотношений

. (6)

Как следует из формул (2, 3, 4), подбор требуемой величины или производится путём расчёта смещения щели или угла наклона . Очевидно, что при изменении частоты резонансная антенна будет рассогласовываться, поскольку меняется относительная длина щели и расстояние между ними . Рассогласование проявляется тем резче, чем больше щелей в антенне.

В нерезонансной антенне расстояние между щелями не кратно 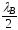, а в конце волновода помещается поглощающая нагрузка. В этом случае в волноводе устанавливается режим, близкий к режиму бегущей волны, и входное сопротивление антенны мало изменяется от частоты. Часть мощности в нерезонансной антенне поглощается в оконечной нагрузке.

При увеличении частоты главный лепесток ДН нерезонансной антенны поворачивается в сторону нагрузки, а при уменьшении – в сторону генератора, т.е. происходит частотное сканирование луча, хотя сектор сканирования невелик для прямолинейной линии передачи (волновода).

В резонансной антенне, работающей в режиме стоячей волны, ДН формируется и падающей, и отражённой волной. В точке резонанса обе ДН совпадают, и главный лепесток ориентирован по нормали. При изменении частоты ДН по падающей и отражённой волне получают противоположное смещение так, что главный лепесток вначале расширяется, а при значительной частотной расстройке – раздваивается. Амплитуды этих отклонённых лепестков будут различными, т.к. отражённая волна имеет меньшую мощность, чем падающая.

ДН антенны из щелей в плоскости оси волновода определяется соотношением

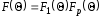, (7)

где – ДН одиночной щели, рассчитываемая по формулам (5) и (5а),

– множитель равномерной линейной решётки.

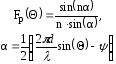, (8)

где отсчитывается от нормали к решётке (рис. 3) ( – к нагрузке, 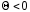– к генератору (приёмнику)),

– расстояние между щелями,

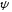– сдвиг фаз питания:

. (9)

Рис. 3

Дополнительный фазовый сдвиг 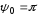обусловлен противоположным смещением соседних щелей, возбуждающих элементов или углов наклона щелей. Если положение щелей и их ориентация одинаковы, то . Длина волны в волноводе для основного типа колебаний определяется по формуле

(10)

Множитель решётки имеет многолепестковый характер. Он является периодической функцией обобщённого аргумента с периодом . На рис. 4 изображён для .

Рис. 4

Как видно, между двумя главными максимумами находятся боковых лепестков, а их величина уменьшается к середине интервала. Для вещественных углов излучения , соответствующих реальному пространству, где , аргумент принимает определённые значения:

. (11)

Эти границы определяют «видимую часть» множителя решётки (заштрихованная область на рис. 4), т.е. каждая точка из этой области соответствует угловому направлению в реальном пространстве.

. (12)

«Видимая часть» множителя решётки позволяет быстро оценить форму ДН и рассчитать характерные точки. Так, из примера на рис. 4 следует, что решётка работает в однолучевом режиме (один главный максимум в видимой части), а характерные угловые точки можно рассчитать по формуле (12). Например, максимум главного лепестка , ; нули главного лепестка , ; ; максимум бокового лепестка справа ; , . Таким же образом из графика «видимой части» можно определить и другие характерные точки – нули и максимумы других боковых лепестков или побочных главных максимумов, если они входят в «видимую часть».

Как уже отмечалось, антенна с наклонными щелями излучает поле с горизонтальной и вертикальной поляризациями по вектору Е. При междуэлементных расстояниях 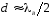поля с горизонтальной поляризацией суммируются синфазно вблизи нормали к антенне, образуя главный лепесток ДН по главной (основной) поляризации. Вертикальные составляющие противофазны вблизи нормали, но могут синфазно суммироваться в областях близких к плоскости решетки, определяя ДН по паразитной (кросс) поляризации.

Более подробные сведения о щелевых антеннах содержатся в литературе [1 – 3].