4. Расчет равновесной концентрации носителей заряда

Как определить концентрацию носителей в заданном полупроводнике при заданной температуре? Это важнейшая задача статистической физики. Для решения этой задачи необходимо знать число квантовых состояний в заданном интервале энергий и вероятность нахождения частиц в этих состояниях. Следовательно, для определения концентрации носителей заряда в полупроводнике необходимо знать фактическое число состояний занятых электронами и дырками.

Графическая интерпретация расчета концентрации носителей заряда в собственном полупроводнике представлена на рис. 7.

Рис. 7 I – это энергетическая (зонная) диаграмма собственного полупроводника.

В теории твердого тела показывается, что энергетические уровни распределены по высоте разрешенной зоны неравноменно: плотность их меняется от границы в глубь зоны

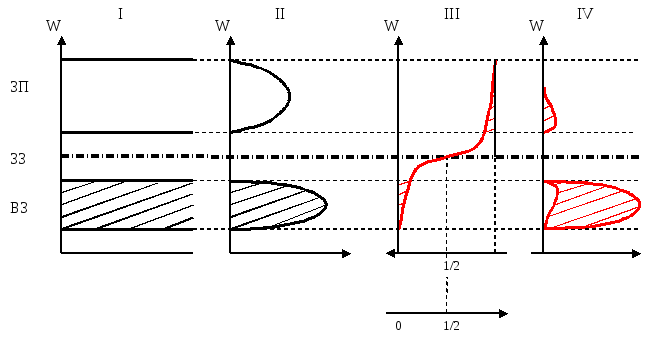
Рис. 7 Графическая интерпретация расчета концентрации носителей заряда в собственном полупроводнике

Обозначим через N(W)– плотность состояний, т.е. число квантовых состояний в единичном интервале энергии для единичного объема кристалла (рис.7II). Наиболее простым частным случаем будет идеальный (безпримесный), другими словами, собственный, кристалл полупроводника, находящийся при температуре абсолютного нуляТ = 0. В этом случае все возможные уровни в валентной зоне будут заполнены электронами, в зоне проводимости нет электронов и распределение электронов по энергиям будет строго соответствовать закону изменения плотности разрешенных уровней (на рис. 7IIэто распределение заштриховано).

С ростом температуры некоторое количество электронов покидает валентную зону и переходит на уровни зоны проводимости. Возникает вопрос: какова вероятность того, что тот или иной уровень валентной зоны лишится электрона и превратится в дырку? Ответ на этот вопрос дает статистика Ферми-Дирака.

Согласно статистике Ферми-Дирака вероятность того, что состояние с энергией Wпри заданной температуреТ занято электроном, выражается функцией Ферми для электронов

,

где k – постоянная Больцмана,Т – абсолютная температура,W_F – энергия, называемая уровнем Ферми.

Вероятность выражается в долях единицы (рис. 7 III). Имеется только две возможности: уровень занят электроном или уровень не занят электроном. Вероятность того, что уровень валентной зоны не занят электроном, есть вероятность нахождения на этом уровне дырки. Сумма вероятностей этих событий должна быть равна 1:(обратите внимание на масштаб осейина рис. 7III). Функция Ферми для дырок

.

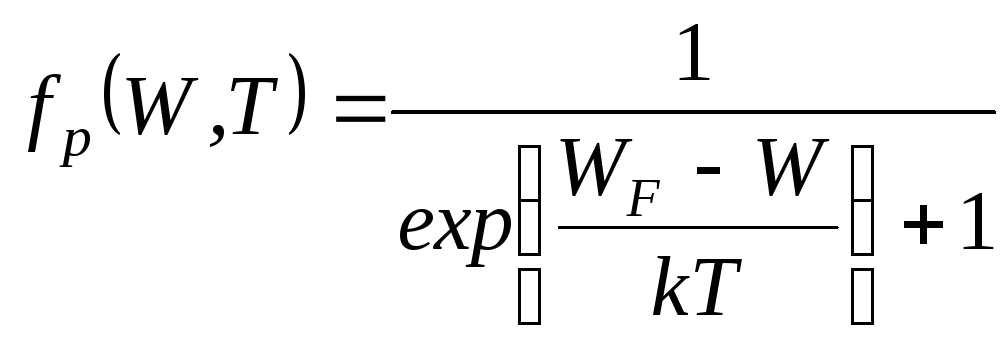При Т = 0 функция Ферми имеет вид ступеньки и показывает, что все энергетические состояния превышающие уровень Ферми свободны, а все энергетические состояния ниже уровня Ферми – заняты.

.

С ростом температуры функция Ферми превращается в плавную (симметричную) кривую (рис. 7 III). Вероятность нахождения электрона в зоне проводимости становится отличной от нуля, а в валентной зоне становится отличной от нуля вероятность появления свободных уровней – дырок. Т.к. эта кривая симметрична, то эти вероятности равны.

Количество электронов, занимающих разрешенные уровни в некоторой элементарной полосе с плотностью уровнейN(W), определяется числом разрешенных уровней в данной элементарной полосеN(W)·и вероятностью их заполнения.

.

Следовательно, количество электронов, находящихся в зоне проводимости равно

,

а число дырок в валентной зоне

.

После преобразований можно получить следующий результат: концентрация электронов n_i будет определяться выражением

,

а концентрация дырок p_i –

.

Здесь – эффективная плотность разрешенных состояний в зоне проводимости, а – эффективная плотность разрешенных состояний валентной зоны,m^*_nиm^*_p– эффективные массы электрона и дырки соответственно,h– постоянная Планка.

Если подставить численные значения универсальных констант, то будем иметь: .

Если положить m^*_n=m^*_p = m₀ , то при Т = 300 КN_C =N_V ≈ 2,5·10¹⁹см^-3. Это составляет приблизительно 1/2000 числа атомов в 1 см³.

Распределения электронов и дырок по энергиям представлено на рис. 7 IVиз которого видно, что эти распределения носителей заряда по энергиям носят экспоненциальный характер. С ростом энергии число электронов в зоне проводимости быстро уменьшается. ПриТ = 300 К основная часть электронов проводимости имеет энергию близкую к энергии дна зоны проводимости, дырки проводимости имеют энергию близкую к энергии потолка валентной зоны.

Равновесная концентрация носителей заряда зависит от температуры

,

причем экспонента является определяющим множителем в этом выражении. Приблизительно можно считать, что n_iбудет возрастать на (5–7)% при увеличении температуры на 1 градус.

Равновесная концентрация носителей заряда зависит от ширины запрещенной зоны полупроводника (табл. 3): чем больше ширина запрещенной зоны, тем меньше равновесная концентрация.

Таблица 3

Равновесная концентрация носителей при комнатной температуре

	Германий	Кремний	Арсенид галлия
ni, см-3	2,5 1013	1,4 1010	1,5 106

Можно сделать следующие выводы:

1. Собственный полупроводник –беспримесный полупроводник.

2. Дырка – это разорванная ковалентная связь, ведущая себя как подвижный носитель заряда, равный по модулю заряду электрона или незаполненный уровень валентной зоны.

3. Энергетический спектр твердого тела состоит из дискретных разрешенных зон. Все существенные процессы в полупроводниковых приборах можно изучить, рассматривая только две смежные зоны: зону проводимости и валентную.

4. При Т = 300 К основная часть электронов имеет энергию близкую к энергии дна ЗП, а дырок - энергию близкую к энергии потолка ВЗ.

5. Распределения носителей заряда по энергиям носят экспоненциальный характер.

6. Равновесная концентрация носителей заряда зависит от ширины запрещенной зоны полупроводника: чем больше ширина запрещенной зоны, тем меньше равновесная концентрация.

7. Равновесная концентрация носителей заряда экспоненциально зависит от температуры.