Лекция 8. Поляризация электромагнитных волн

8.1. Поляризация плоских однородных волн

Поляризацией электромагнитной волны называют изменения величины и ориентации векторов и в фиксированной точке пространства в течение периода колебания волны. Волна, у которой в фиксированной точке пространства в любой момент времени величина и ориентация векторов и являются детерминированными (точно определенными), называется поляризованной. Поляризация волны ориентационная характеристика. В плоской однородной волне векторы и взаимосвязаны (6.36), характер их поведения в пространстве одинаков, поэтому ограничиваются рассмотрением одного вектора . Плоскость, проходящую через вектор и направление распространения волны, называют плоскостью поляризации.

Предположим, что волна создается двумя взаимно перпендикулярными элементарными электрическими вибраторами с токами и (рис. 8.1).

Рис. 8.1. К введению понятия поляризации волны

Вектор имеет две составляющие Е_х и Е_у, которые имеют разные амплитуды и изменяются с некоторым фазовым сдвигом в зависимости от соотношения между амплитудами и фазами токов вибраторов. Вектор при этом также имеет две составляющие Н_х и Н_у, связанные с Е_х и Е_у характеристическим сопротивлением. Таким образом, в общем случае выражение для вектора плоской волны в среде без потерь записывается в виде

. (8.1)

Здесь и – начальные фазы составляющих Е_х и Е_у в точке z = 0 при t = 0. Волну (8.1) можно рассматривать как суперпозицию(сумму) двух плоских волн одинаковой частоты с взаимно перпендикулярной ориентацией векторов и , распространяющихся в одном направлении (вдоль оси z). Определим ориентацию суммарного вектора (8.1) углом (рис. 8.2).

Рис. 8.2. Мгновенное положение вектора

Угол отсчитывается по часовой стрелке, если смотреть вдоль направления распространения волны и определяется соотношением

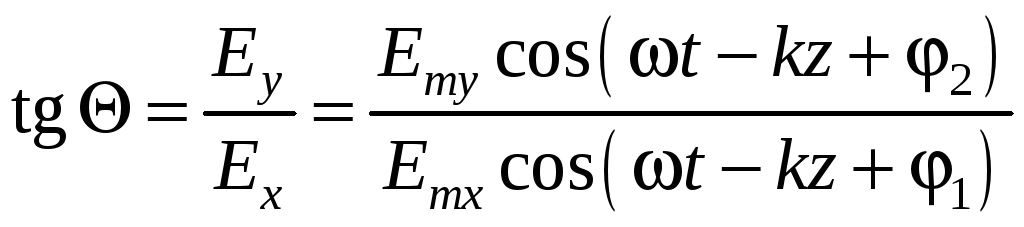. (8.2)

Характер изменения вектора (8.1) с течением времени в фиксированной точке пространства зависит от сдвига фаз и от равенства или неравенства амплитуд и . В общем случае угол может изменяться во времени. Конец вектора с течением времени в фиксированной точке пространства будет описывать линию, называемую годографом. По форме годографа выделяют три вида поляризации.

1. Линейная поляризация. Составляющие Ех и Еу синфазны или противофазны

, где n = 0,1,2,… (8.3).

Для простоты возьмем n = 0, то есть начальные фазы и совпадают. Полагая в формуле (8.2) , получаем постоянное значение угла ориентации

. (8.4)

Величина вектора (8.1) меняется во времени

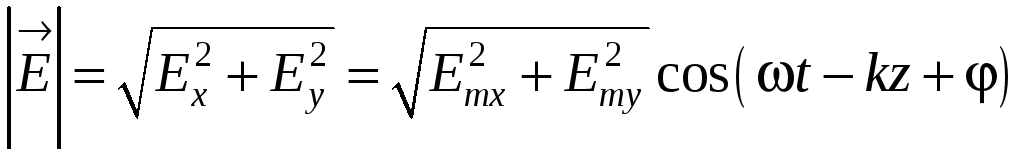. (8.5)

В фиксированной точке пространства вектор , не меняя ориентации ( = const) изменяется по модулю, конец вектора с течением времени перемещается вдоль отрезка прямой линии, составляющей с осью х угол

. (8.6)

При четных значениях числа n (Е_х и Е_у синфазны) угол величина положительная; при нечетных n (Е_х и Е_у противофазны) угол величина отрицательная. Таким образом, волна (8.74) при выполнении условия (8.3) имеет линейную поляризацию. Отметим, что если вектор плоской волны имеет одну составляющую, волна линейно поляризована.