Рекурсия Основные определения

Рекурсия – это способ определения объекта, при котором он частично определяется через такой же объект. Определение, содержащее рекурсию, называется рекурсивным определением. Например, натуральное число – это либо 1, либо целое число, следующее за натуральным.

Рекурсивно можно определять не только объекты, но и математические функции. Функция называется рекурсивной, если ее значение при некоторых значениях аргументов определяется через значение этой функции при других значениях аргументов. Например:

В программировании рекурсия – это описание функции, содержащее прямой или косвенный вызов этой подпрограммой самой себя. Если функция р вызывает себя в своем теле, то такая рекурсия называется прямой, если же подпрограмма р вызывает подпрограмму q, которая прямо или косвенно вызывает р, то такая рекурсия называется косвенной. Рекурсией также называют процесс выполнения рекурсивной функции.

Простые примеры использования рекурсии

Рассмотрим несколько примеров рекурсивных функций.

Пример 1.

void re_1();

void main()

{

re_1();

}

void re_1()

{

cout<<'1'<<endl;

re_1();

}

При вызове процедуры p произойдёт рекурсивное зацикливание: будет выводиться 1, после чего процедура снова будет вызывать себя и т.д. до бесконечности. Поскольку при каждом вызове процедуры на программный стек помещается ее запись активации, то в конце концов, программный стек переполнится, и программа завершится с ошибкой. Таким образом, чтобы рекурсия завершалась, необходимо, чтобы рекурсивный вызов происходил не всегда, а лишь при выполнении некоторого условия.

Пример 2.

#include <iostream>

using namespace std;

void re_2(int);

void main()

{

re_2(5);

}

void re_2(int n)

{

cout<<n<<' '<<endl;

if (n>0) re_2(n-1);

}

При вызове re_2(5) вначале выведется 5, после чего вызовется re_2(4), выведется 4 и вызовется re_2(3) и т.д. до вызова re_2(0), который выведет 0 и, поскольку условие n>0 станет ложным, рекурсия завершится. Итак, в результате вызова re_2(5) на экран будет выведено

5 4 3 2 1 0

Таким образом, использование рекурсии позволяет заменить цикл. Отметим, что в простых примерах такая замена неэффективна, так как накладные расходы на рекурсивный вызов процедур (копирование параметров на программный стек, запоминание адреса возврата и т.д.) намного превосходят затраты на организацию цикла.

Пример 3.

void p(int n)

{

if (n>0) p(n-1);

cout<<n<<' '<<endl;

}

При вызове p(5) вначале проверится условие n>0 и, поскольку оно истинно, вызовется p(4), затем p(3) и т.д. до p(0). Так как при вызове p(0) условие n>0 уже не выполняется, то осуществится вывод 0 и произойдет выход из вызова p(0) в вызов p(1) сразу после условного оператора. Далее осуществится вывод 1 и выход из вызова p(1). Процесс возврата из уже сделанных рекурсивных вызовов продолжится, пока не будет осуществлен выход из вызова p(5). В результате на экран будет выведено

0 1 2 3 4 5

Схема рекурсивных вызовов в примерах 2 и 3 изображена на рисунке:

Процесс рекурсивных вызовов называется рекурсивным спуском, а процесс возврата из них – рекурсивным возвратом. Глубиной рекурсии называется максимальное число вложенных рекурсивных вызовов (в примерах 2 и 3 глубина рекурсии равна 5). Число вложенных рекурсивных вызовов в данный момент выполнения программы называется текущим уровнем рекурсии.

Отметим, что в примере 2 действия осуществляются на рекурсивном спуске, поэтому порядок действий – прямой (в порядке вызова рекурсивных процедур). В примере 3, напротив, действия осуществляются на рекурсивном возврате, т.е. откладываются до достижения наивысшей глубины рекурсии, после чего начинают выполняться в порядке, обратном порядку вызова.

Реализуем рекурсивные функции из примеров в начале пункта.

Пример 4. Вычисление n!

int Nfact(int);

void main()

{

cout<<"n! = "<<Nfact(5)<<endl;

}

int Nfact(int n)

{

cout<<n<<' '<<endl;

if (n==0) return 1;

else return n*Nfact(n-1);

}

Пример 5. Вычисление .

Рассмотрим рекурсивное определение , которое является более эффективным и, кроме того, учитывает случай :

Реализация также не вызывает затруднений:

double Power(double, int);

void main()

{

cout<<"a^n = "<<Power(5,3)<<endl;

}

double Power(double a, int n)

{

cout<<n<<' '<<endl;

if (n==0) return 1;

else if (n<0) return Power(a,-n);

else if (n%2) return a*Power(a,n-1);

else return pow((Power(a,n/2)), 2);

}

При программировании рекурсивных функций следует следить за глубиной рекурсии: она не должна быть очень большой, чтобы программный стек не переполнился.

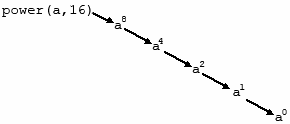
Нетрудно видеть, что при вычислении глубина рекурсии равна 5:

При вычислении же функция Power последовательно вызывается для аргументов 15, 14, 7, 6, 3, 2, 1, 0, и глубина рекурсии составляет 7. 

Недостаток данного алгоритма состоит в том, что переменная a не меняется, но передается в каждый рекурсивный вызов. Сделаем переменную a глобальной по отношению к рекурсивной функции, например:

Пример 6.

int a;

double Power0(int);

void main()

{

a = 5;

cout<<"a^n = "<<Power0(3)<<endl;

}

double Power0(int n)

{

cout<<n<<' '<<endl;

if (n==0) return 1;

else if (n<0) return Power0(-n);

else if (n%2) return a*Power0(n-1);

else return pow((Power0(n/2)), 2);

}

Пример 7. Минимум в массиве.

Чтобы найти минимум в массиве из n элементов, достаточно найти минимум в массиве из первых n – 1 элементов, после чего выбрать минимальный из этого минимума и последнего элемента массива. Если в массиве всего один элемент, то он – минимальный.

Запишем данный алгоритм в виде рекурсивной функции MinA:

Реализация повторяет рекурсивное определение:

int a[]={45,2,3,4,654,3,2,1,4,-1,0,23};

int MinA(int);

void main()

{

cout<<"min a[] = "<<MinA(sizeof(a)/sizeof(int))<<endl;

}

int MinA(int n)

{

if (n==1) return a[n];

else {

int m =MinA(n-1);

if (a[n]<m) return a[n];

else return m;}

}

Сделаем несколько замечаний, касающихся рекурсивных функций.

Замечание 1. При каждом рекурсивном вызове на программный стек помещается запись активации подпрограммы. Поэтому если количество рекурсивных вызовов большое или локальные переменные рекурсивной процедуры имеют большой размер, то программный стек может переполниться и возникнет ошибка времени выполнения программы.

Замечание 2. Накладные расходы на рекурсивные вызовы достаточно велики, поэтому если есть явное нерекурсивное решение, то следует предпочесть его.

Замечание 3. Можно доказать, что любая прямая рекурсия может быть заменена итерацией.