5.10. Адаптивная дискретизация

Если ранее рассмотренные методы и алгоритмы дискретизации были рассчитаны на все множество возможных реализаций сигнала и потому опирались на предельные значения его динамических характеристик, то при адаптивной дискретизациимы ориентируемся на динамические характеристики конкретной реализации, что позволяет получить минимальное число выборок, обеспечивающих восстановление этой реализации с заданной точностью.

В основе принципа адаптивной дискретизации лежит непосредственное слежение за текущей погрешностью восстановления сигнала ε.

Наиболее широкое применение на практике получили алгоритмы дискретизации с адаптацией по длине интервала аппроксимации. В процессе последовательного наращивания интервала аппроксимации производится сравнение сигнала u(t) с воспроизводящей функциейu*(t),формируемой с учетом текущих значений динамических характеристик сигнала. Когда погрешность воспроизведения достигает заданного значенияε₀, наращивание интервала прекращается и производится отсчет. Интервалы времени между отсчетами при этом оказываются произвольными.

Вкачестве воспроизводящих функций наиболее часто используются степенные алгебраические полиномы нулевой и первой степеней.

а б

Рис.5.10. Адаптивная дискретизация

При этом возможны как интерполяционные, так и экстраполяционные способы адаптивной дискретизации. Интерполяционные способы не нашли широкого применения, поскольку их реализация связана с запоминанием сигнала на интервале аппроксимации и выполнением большого числа вычислительных операций. Поэтому ограничимся рассмотрением примеров адаптивной дискретизации на основе экстраполяции.

Пример.Провести адаптивную дискретизацию реализации сигналаи(t),изображенной на рис.5.10,а, с использованием аппроксимирующего многочлена нулевой степени. Наибольшее допустимое отклонение равноε₀.

На момент t_jначала каждого интервала аппроксимирующий полиноми*(t) принимаем равнымu(t_j) и вычисляем разность Δu(t)=u(t)-u*(t_j),которую сравниваем сε₀. Установление равенства

|Δu(t)|= ε0

соответствует моменту t_j+1окончания интервала и проведения очередного отсчета.

Результаты дискретизации отображены на том же рисунке.

Пример. Провести адаптивную дискретизацию реализации сигналаи(t),изображенного на рис.5.10,б, многочленом первой степени. Наибольшее допустимое отклонение равноε₀.

На момент tj начала каждого интервала аппроксимации

u*(t)=u(t_j)+u'(t_j)t,

где u'(t_j) —производная сигналаи(t) в момент времениt_j.

Момент очередного отсчета определяется выполнением равенства

Δu(t)=u(t)-u(tj)-u'(tj)t=ε0.

Результаты дискретизации приведены на том же рис. 5.10. При аппаратной реализации данного алгоритма следует иметь в виду, что вследствие наличия операции дифференцирования сигнала он неэффективен при наличии высокочастотных помех.

5.11. Квантование сигналов

Поскольку математической моделью непрерывного сигнала является случайный процесс U(t),мгновенное значение сигналаU=U(t) представляет собой случайную величину. Диапазон ее изменения, называемый непрерывной шкалой мгновенных значений сигнала, ограничен значениямиU_minиU_max, что отражает условие физической реализуемости сигнала.

Непрерывную шкалу мгновенных значений U_n=U_max  U_minсигнала разбивают наiинтервалов, называемыхшагами квантования.Границами шагов квантования являются значенияU₀= U₁,...,U_n-1,U_n=U_max. Из множества мгновенных значений, принадлежащихi-му шагу квантования (U_i-₁ <U< U_i ), только одно значениеU'₁,является разрешенным (i-й уровень квантования). Любое другое из указанного множе­ства значений округляется доU'i.Совокупность величинU'_i(i= 1, 2, ...,п) образует дискретную шкалу уровней квантования. Если эта шкала равномерна, т. е. разность значенийΔU'_i=U'_i,— U'_i-₁постоянна на всем протяжении непрерывной шкалы мгновенных значений сигналаи,квантование называютравномерным.Если постоянство значе­нийΔU'iне выдерживается, то квантованиенеравномерное. Благодаря простоте технической реализации равномерное квантование получило наиболее широкое распространение.

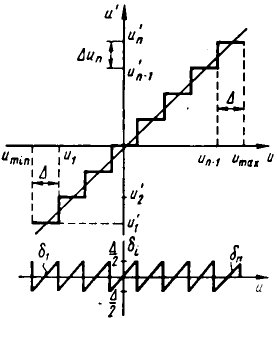
Рис. 5.11. Квантование сигнала

В результате замены мгновенного значения сигнала U соответствующим уровнем квантованияΔU'_iвозникает по­грешностьΔ=U—U'_i, которую называютошибкой квантования.Эта погрешность является случайной величи­ной. Нас чаще всего интересует ее максимальное значениеΔm=mах|Δ_i| и среднеквадратическое отклонениеΔ для всего диапазона измене­ния мгновенных значений сигнала. Используются также приведенные значения этих величин

Δ_M0= Δ_M/(U_max - U_min),

Δ

Рис.5.13

₀ = Δ/(U_max - U_min)

С позиций минимизации наибольшей возможной ошибки квантования непрерывную шкалу мгновенных значений сигнала целесообразно разбить на подинаковых шагов квантованияΔ=(U_max-U_max)/nи уровни квантования разместить в середине каждого шага (рис. 5.11). При этом максимальная ошибка квантования не превышает 0,5Δ. Если каждый уровень квантования выбран равным нижней (верхней) границе шага квантования, максимальная ошибка квантования возрастает до величиныΔ.

С

(166)

реднеквадратическое отклонение ошибки квантования дляi-го шагаΔ_i, зависит не только от шагаΔи расположения в немi-го уровня квантования, но и от закона распределения мгновенных значений сигнала в пределах этого шага:

где р(U) —функция плотности вероятности мгновенных значений сигналаU.

Рис. 5.12. Ошибка равномерного квантования

(44)

Шум квантования. При квантовании сигнала по уровню случайный процесс заменяется ступенчатой зависимостьюV(t).Изменяющуюся во времени ошибку квантования, также представляющую собой случайный процесс, называютшумом квантования:

(45)

Δ(t)=U(t)-U’(t)

С

охраняя ранее введенные предположения (о малости ша­га квантования и равномернос­ти распределения в нем мгно­венных значений сигнала) и считая случайные процессыU(t) иΔ(t) эргодическими, среднеквадратическую ошибку рав­номерного квантования о мож­но определить по реализацииΔ₁(t) (рис.5.12). В пределах каждого шага квантованияΔзависимостьΔ₁(t) заменяется прямойttgβ_i, гдеβ- перемен­ный угол наклона прямой. При размещении уровней квантования в

Рис.14

середине каждого шага математическое ожидание ошибки квантования равно нулю, а ее среднеквадратическое значение определяется выражением

(167)

(46)

Так как tgβ=Δ/T, тоΔ=Δ/23 что соответствует ранее полученному значению.

(47)

П

(168)

ри заданной допустимой среднеквадратической ошибке квантования и отсутствии помех число уровней квантования находим из соотношения

Однако при неравномерном законе распределения мгновенных значений сигнала квантование с постоянным шагом не является оптимальным по критерию минимума среднеквадратической ошибки. Квантуя участки с ме­нее вероятными значениями сигнала с большим шагом, указанное значение среднеквадратической ошибки можно уменьшить.