5.6.2. Теорема Котельникова

Теорема устанавливает принципиальную возможность полного восстановления детерминированной функции с ограниченным спектром по ее отсчетам и указывает предельное значение интервала времени между отсчетами, при которой такое восстановление еще возможно. Она формулируется следующим образом: функция u(t),допускающая преобразование Фурье и имеющая непрерывный спектр, ограниченный полосой частот от 0 доF_c=_C/(2), полностью определяется дискретным рядом своих мгновенных значений, отсчитанных через интервалы времени

Физическая основа теоремы выявляется при рассмотрении связи между формой функции и шириной ее спектра. Только в случае, когда спектр функции безграничен, ее значения в сколь угодно близкие моменты времени могут изменяться произвольно (корреляционная связь между ними отсутствует). Сокращение высокочастотной части спектра до граничной частоты ₁равнозначно устранению из временной функции выбросов, которые могли быть сформированы этими высокочастотными составляющими (рис5.2,а). При меньших граничных частотах₂(рис.5.2,б) и₃(рис.5.2,в) имеем более сглаженные функции времени. Поскольку значения этих функций в моменты времениu(t₁) иu(t₁+t) в пределах некоторого интервалаtне могут изменяться существенно, можно ограничиться значениями функции, взятыми через интервалыt(отсчетами).

Рис.5.2.

В результате сложных вычислений, окончательно получим

(147)

Итак, функция u(t) выражена через ее дискретные значения, взятые в моменты времениt_n=nΔt=nπ/ω_c.

Так как при любых целых k и п справедливы соотношения

ω_c(kΔt-nΔt)=(k-n)ω_cΔt=(k-n)π ,

то

(148)

Благодаря этому свойству значения функции u(k) в моменты времениt_n= nΔtпредставляют собой не что иное, как ее отсчеты.

Представление функции u(t) в виде ряда (147) (ряда Котельникова) является частным случаем разложения

Роль коэффициентов С_kвыполняют отсчетыu(nΔt) функцииu(t).Базисными являются функции вида

(149)

Они называются функциями отсчетов.

Графики этих функций прип=0 ип=1 приведены на рис.5.3. Каждая функцияψ_n(t) имеет неограниченную протяженность во времени и достигает своего наибольшего значения, равного единице, в момент времениt=nπ/ω_c;относительно этого момента времени она симметрична. В моменты времениt=kπ/ω_c,гдеkп, функция обращается в нуль. Все функции ортогональны между собой на бесконечно большом промежутке времени, что легко проверяется путем вычисления интеграла:

(150)

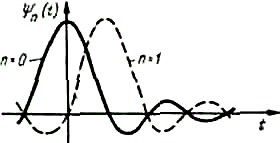
Рис.5.3. Графики функций отсчетов

Каждую функцию отсчета можно рассматривать как реакцию (отклик) идеального фильтра нижних частот с граничной частотой fcна дельта-импульс, приходящий в момент времениt_n=nΔtи имеющий площадь, равнуюu(nΔt).

Теорема Котельникова распространяется на непрерывный в среднеквадратическом смысле стационарный случайный процесс с ограниченным энергетическим спектром (S_n(ω)=0 при|ω|>ω_П=2πF_п).

Такой процесс представляется суммой квазидетерминированных процессов, где роль ортогональных детерминированных функций выполняют функции отсчета, а случайных коэффициентов — величины выборок: