Перевод чисел из одной системы счисления в другую

Сначала рассмотрим перевод из двоичной системы счисления в шестнадцатеричную и наоборот. Это наиболее просто в связи с тем, что 16 = 2⁴.

Правило 1. Для перевода шестнадцатеричного числа в двоичное надо каждую цифру заменить четырехразрядным двоичным числом. Незначащие нули отбросить.

Пример 10

305,4₁₆ =0011 0000 0101,0100₂ =1100000101,01₂

Правило 2. Для перевода числа из двоичной системы счисления в шестнадцатеричную надо число разбить на четверки влево и вправо от запятой. Крайние группы, если необходимо дополнить нулями. Затем каждую четверку двоичных цифр заменить соответствующей шестнадцатеричной цифрой.

Пример 11

1010111,1101101₂ =0101 0111,1101 1010₂ =57,DA₁₆

Рассмотрим общие правила перевода чисел из одной системы счисления в другую. Эти правила зависят от того, в какой системе счисления осуществляются арифметические операции, связанные с преобразованием чисел, - в той, в какой представлено исходное число, или в той, в которую оно переводится.

Правило 3. Задано число С, представленное в системе счисления с основанием S: C = C_n C_n-1 …C₁ C₀ C_-1 C_-m . Нужно перевести его в h-систему, выполняя действия в новой системе счисления.

Для этого нужно представить его в виде суммы степеней S :

C = C_n Sⁿ +C_n-1 S^n-1 +…+C₁ S¹ +C₀ S⁰ +C_-1 S^-1 +…+C_-m S^-m,

где основание S, коэффициенты С и номера разрядов i выражены в новой h-системе. Все действия надо выполнять в h-системе.

Пример 12

1. Перевести 2Е5,А₁₆ в десятичную систему счисления:

2Е5,А₁₆ =2 16² +1416¹ +516⁰ +1016^-1 =741,625₁₀.

2. Перевести 52₁₀ в двоичную систему счисления:

52₁₀=1011010¹ +101010⁰ =110010+10=110100₂.

3. Перевести 1101,101 в десятичную систему счисления:

1101,101₂ = 1 2³ +1 2² +0 2¹ +1 2⁰ +1 2^-1 +0 2^-2+1 2^-3 =13,625₁₀.

Этот способ удобен при S < h и особенно для ручного перевода в десятичную систему счисления.

Рассмотрим перевод целого числа С из S-системы в h-систему в арифметике S-системы счисления.

Правило 4. Для перевода целого числа из S-системы в h-систему счисления в арифметике S-системы нужно последовательно делить это число и получающиеся частные на h до тех пор, пока частное не станет меньше h. Старшей цифрой в новой записи числа будет последнее частное, а следующие за ней цифры дают остатки, вписанные в последовательность, обратную их получению. Все вычисления производятся в старой S-системе. (При S<h прежде, чем записать число, надо получившиеся остатки переписать в цифры h-системы).

Приме 13

1. Перевести число 70 в двоичную систему счисления

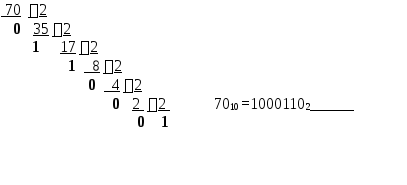
Прямой, обратный и дополнительный коды чисел

В ЭВМ с целью упрощения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов:

• автоматически определяется знак результата;

• операция вычитания сводится к арифметическому сложению кодов чисел;

• упрощается операционная часть ЭВМ.

В ЭВМ используется прямой, обратный и дополнительный коды чисел. Знак “+” кодируется нулем (0), “-” - единицей (1), которые записываются в дополнительном старшем разряде - знаковом разряде.

Возьмем целое число С = + C_n C_n-1 C_n-2 ...C₁ C₀ .

1. Прямой код для целых чисел определяется:

.

Для отрицательных двоичных чисел имеем:

C = 2 +-C_n C_n-1 ...C₀ = 1.C_n C_n-1 ...C₀,

где точкой отделен знаковый разряд.

Таким образом, для получения прямого кода числа надо в знаковый разряд записать 0 для положительных и 1 для отрицательных чисел.

C = +10110, C_пр = 0.10110; C = -10110, C_пр = 1.10110.

Сложение в прямом коде не вызывает затруднений, когда у слагаемых одинаковые знаки: сложить модули и сумме присвоить знак слагаемых. При вычитании чисел в прямом коде нужно сначала определить больший модуль, от него отнять меньший и результату присвоить знак большего модуля.

2. Обратный код определяется:

.

Для отрицательных двоичных чисел имеем:

C_обр = 2ⁿ⁺² - 1 --C_n C_n-1 …C₀ = 11…1 – 0.C_n C_n-1…C₀= 1._{n n-1}…_0,

где _I = 1 при C_i = 0 и _I = 0 при C_i = 1 .

Таким образом, для представления чисел в обратном коде надо в знаковый разряд записать 0 или 1, для отрицательных чисел в значащие разряды нужно записать дополнение модуля исходного числа до наибольшего числа без знака, помещающегося в данных разрядах. Для двоичной системы счисления последнее означает, что в случае отрицательных чисел для получения обратного кода надо значение разрядов инвертировать: вместо 0 записать 1, вместо 1 – 0.

C = +10110, C_обр = 0.10110; С = -10110, С_обр = 1.01001.

2. Дополнительный код чисел определяется:

.

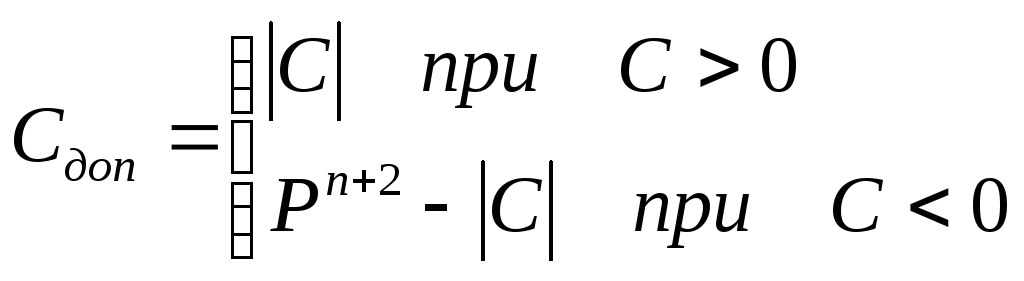При представлении двоичного отрицательного числа в дополнительном коде в знаковый разряд надо записать 1, а цифровую часть заменить дополнением числа до 2ⁿ⁺¹ .

Сравним выражения для представления обратного и дополнительного кода числа. Становится очевидно, что дополнительный код отрицательных чисел получается из обратного прибавлением единицы в младший разряд.

C_доп = С_обр +1, при С < 0 .

C = +10110, C_доп = 0.10110; С = -10110, С_доп = С_обр+1 = 1.01001+1 = 1.01010.

Как можно увидеть, при вычислениях в ЭВМ в прямом и обратном коде может получиться как положительный, так и отрицательный нуль (+0, -0).

(+0)_пр=0,00…0, (-0)_пр=1,00..0;

(+0)обр=0,00…0, (-0)_обр=1,11…1.

И только в дополнительном коде нуль представляется однозначно:

(+0)_доп = 0,00…0, (-0)_доп = 1,11…1+2^-m = 0.

Нетрудно доказать, что (по модулю):

• Обратный код от обратного кода дает прямой код числа.

• Дополнительный код от дополнительного кода дает прямой код числа.