Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет – УПИ имени первого Президента России Б.Н.Ельцина»
В.Н. Круглов
Цифровая обработка изображений
Лабораторный практикум
Екатеринбург
2009
УДК 004.9
Составитель: доц. канд. техн. наук В.Н. Круглов
ЦИФРОВАЯ ОБРАБОТКА ИЗОБРАЖЕНИЙ
Лабораторный практикум по курсу «Цифровая обработка изображений» по направлению 230100 – «Информатика и вычислительная техника» / В.Н.Круглов – Екатеринбург: ГОУ ВПО ВПО «УГТУ-УПИ имени первого Президента России Б.Н.Ельцина», 2009. 69 с.
Лабораторный практикум содержит описание, теоретические положения и методические указания 5 лабораторных работ по курсу «цифровая обработка изображений». За время выполнения практикума студенты должны изучить, запрограммировать и получить практические навыки использования алгоритмов видоизменения гистограмм, пространственной фильтрации, метода медианной фильтрации, а также линейные и нелинейные методы выделения границ областей и операции математической морфологии. Приводятся задания для самостоятельной работы студентов в вычислительной лаборатории.
Библиогр.: 20 назв. Табл. 7. Рис. 47.
ГОУ ВПО «Уральский государственный технический университет – УПИ имени первого Президента России Б.Н.Ельцина»
Лабораторная работа № 1
«Сглаживающие пространственные фильтры»
1. Цель лабораторной работы.
Целью работы является углубление знаний по разделу «Сглаживающие пространственные фильтры» и приобретение практических навыков подавления шумов на изображениях.
2. Теоретическая часть
2.1. Основы пространственной фильтрации
Пространственные фильтры изменяют значения пикселя в зависимости от изменений яркости световой интенсивности его соседних пикселей. Соседние пиксели определяются исходя из размера матрицы, или маски, центр которой приходится на рассматриваемый пиксель.
В случае матрицы 3x3, как показано на нижеследующем рисунке, значение центрального пикселя (показан сплошной заливкой) устанавливается в зависимости от значений восьми окружающих его пикселей (показаны штриховкой).
Рис. 1. Восьмисвязная окрестность
Некоторые локальные преобразования оперируют одновременно как со значениями пикселей в окрестности, так и с соответствующими им значениями некоторой матрицы, имеющей те же размеры, что и окрестность. Такую матрицу называют фильтром, маской, ядром. Значения элементов матрицы принято называть коэффициентами.
2.2. Схема пространственной фильтрации
Процесс основан на простом перемещении маски фильтра от точки к точке изображения; в каждой точке (х, у) отклик фильтра вычисляется с использованием предварительно заданных связей. В случае линейной пространственной фильтрации отклик задается суммой произведений коэффициентов фильтра на соответствующие значения пикселей в области, покрытой маской фильтра. Для маски 3x3 элемента, показанной на рис.2, результат (отклик) R линейной фильтрации в точке {х, у) изображения составит
что, как видно, есть сумма произведений коэффициентов маски на значения пикселей непосредственно под маской.
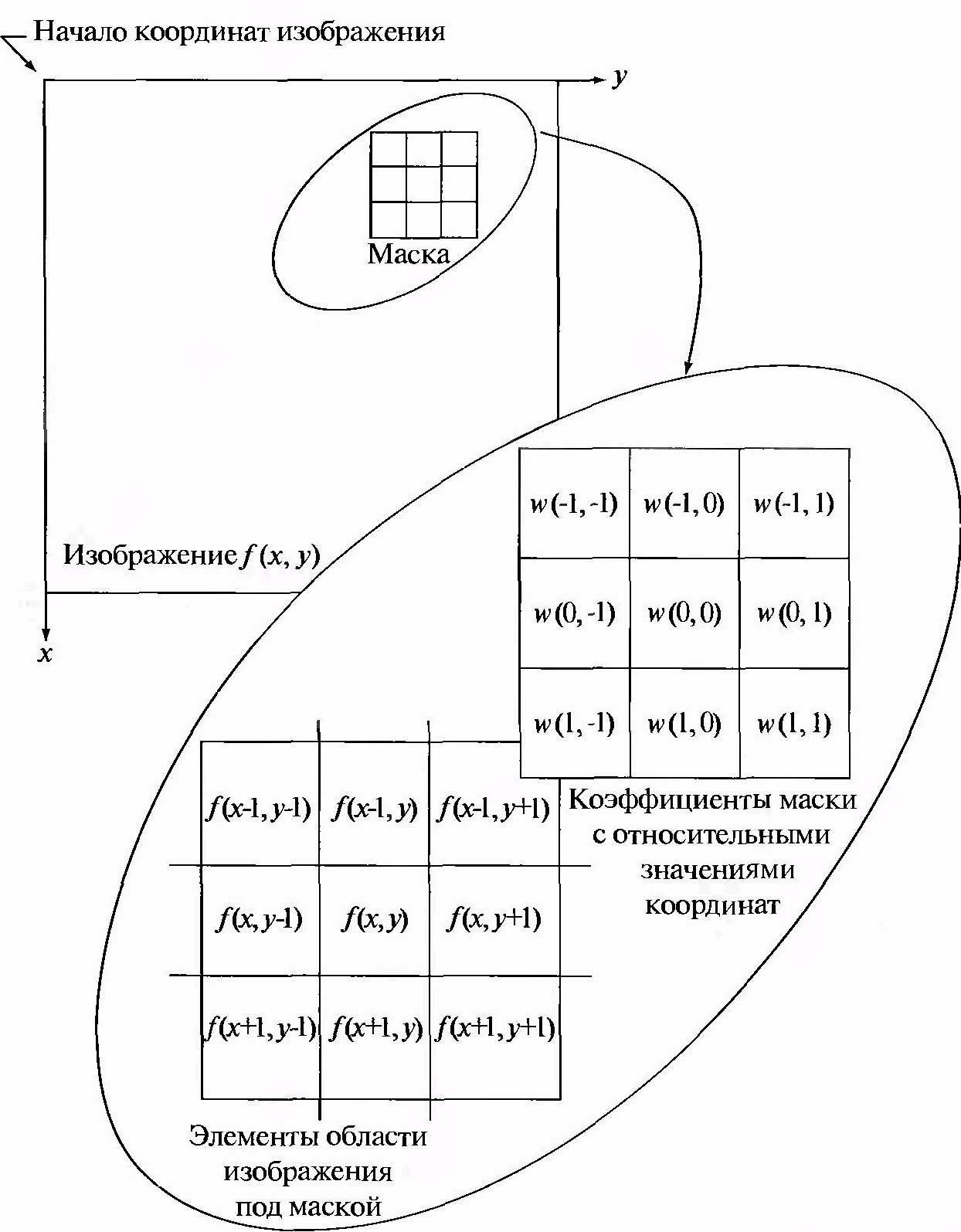
Рис.2. Схема пространственной фильтрации
Фильтрация изображения, имеющего размеры MxN, с помощью фильтра размерами т*п задается выражением общего вида:
Нелинейные пространственные фильтры также работают по окрестности. Схема действий операции нелинейной фильтрации зачастую зависит от значений элементов анализируемой окрестности, и не обязательно должна использовать коэффициенты линейной комбинации.