Фильтрация изображений

Добавление шума

Синтаксис:

Id=imnoise(Is, type, params)

Описание:

Функция imnoiseсоздает новое изображение Id путем добавления шума к исходному полутоновому изображению Is. В основном данная функция предназначена для создания тестовых изображений, используемых при выборе методов фильтрации шума, однако может применяться и для придания фотореалистичности искусственно синтезированным изображениям.

Функция imnoiseможет добавлять шум трех типов. Тип шума задается строковой константой type, которая может принимать одно из следующих значений: -‘gaussian’- для гауссова белого шума; - ‘salt&pepper’ - для импульсного шума (шум типа “соль и перец”); - ‘speckle’ - для мультипликативного шума.

Количество и смысл параметров params определяются выбранным типом шума. Если параметры не указаны, то будут использованы значения по умолчанию.

Id=imnoise(Is, ‘gaussian’, m, v) добавляет к изображению Is гауссов белый шум с математическим ожиданием m и дисперсией v. По умолчанию математическое ожидание равно 0, а дисперсия - 0.01.

Id=imnoise(Is, ‘salt&pepper’, d) добавляет к изображению Is импульсный шум. Параметр d определяет плотность шума и равен доле искаженных пикселов. По умолчанию d=0.05.

Id=imnoise(Is, ‘speckle’, v) добавляет к изображению Is мультипликативный шум Id=Is+n*Is, где n - равномерно распределенный случайный шум с математическим ожиданием 0 и дисперсией v. По умолчанию v=0.04.

Форматы представления данных исходного и результирующего изображений совпадают.

Свертка изображений

Синтаксис:

Z=conv2(X, Y) Z=conv2(hcol, hrow, X) Z=conv2(…, shape)

Описание:

Функция Z=conv2(X, Y)вычисляет свертку Z двух изображений [1], представленных в виде двумерных массивов X и Y. Если эти массивы соответственно имеют размеры mx*my, то размер массива Z равен (mx+my-1)*(nx+ny-1).

Функция Z=conv2(hcol, hrow, X)выполняет свертку двумерного массива X с вектором-столбцом hcol и вектором-строкой hrow.

Функция Z=conv2(…, shape)с помощью параметра shape управляет размером массива Z. Параметр shape может принимать следующие значения: - ‘full’ - полноразмерная свертка; - ‘same’ - центральная часть размера mx*my; - ‘valid’ - центральная часть размера (mx-my+1)*(nx-ny+1) при условии, что (mx*my)>(my*ny).

При использовании значений ‘same’ и ‘valid’ изображение необходимо задавать в параметре X, а коэффициенты фильтра (маску) - в параметре Y. Если используется значение ‘full’, то порядок задания параметров может быть произвольным.

Процедура conv2 выполняется наиболее эффективно при условии, что (mx*my)>(my*ny), т.е. если количество элементов массива X превосходит количество элементов массива Y.

Результирующий массив Z имеет формат представления данных double.

Сопутствующие функции: FILTER2, CONV,CONVN,DECONV.

Задание маски предопределенного типа

Синтаксис:

h=fspecial(type, P1, P2)

Описание:

Функция h=fspecial(type, P1, P2)возвращает маску h предопределенного двумерного линейного фильтра, задаваемого строкой type. Маска h предназначена для передачи в функцииfilter2илиconv2, выполняющих двумерную линейную фильтрацию. В зависимости от типа фильтра для него могут быть определены один или два дополнительных параметра Р1, Р2. Ниже будут рассмотрены возможные варианты функцииfspecial.

Функция h=fspecial(‘gausian’, n, sigma)возвращает маску h фильтра нижних частот Гаусса. Размер маски определяет параметр n. Если n - двухкомпонентный вектор, то размер маски n(1)n(2). Если n скаляр, то размер маски nn. Параметр sigma задает среднеквадратическое отклонение распределения Гаусса, которое используется при формировании маски h. Если при вызове функции параметры n и sigma опущены, то размер маски устанавливается равным 33, а среднеквадратическое отклонение 0.5.

Функция h=fspecial(‘sobel’)возвращает маску фильтра Собеля для выделения горизонтальных границ:

.

Для выделения вертикальных границ достаточно транспонировать данную маску h.

Функция h=fspecial(‘prewitt’)возвращает маску фильтра Превита для выделения горизонтальных границ:

.

Для выделения вертикальных границ достаточно транспонировать данную маску h.

Функция h=fspecial(‘laplasian’, a)возвращает маску h ВЧ фильтра Лапласа. Размер маски 33. Параметрауправляет соотношением между центральным и граничными элементами маски. Данный параметр должен устанавливаться в диапазоне [0, 1]. По умолчаниюа=0.2.

Функция h=fspecial(‘log’, n, sigma)возвращает маску h фильтра, аналогичного последовательному применению фильтров Гаусса и Лапласа, так называемого лапласиана-гауссиана. Размер маски определяет параметр n. Если n - двухкомпонентный вектор, то размер маски n(1)n(2). Если n - скаляр, то размер маски nn. Параметр sigma задает среднеквадратическое отклонение Гаусса, которое используется при формировании маски h. Если при вызове функции параметры n и sigma опущены, то размер маски устанавливается равным 55, а среднеквадратическое отклонение 0.5.

Функция h=fspecial(‘average’, n)возвращает маску h усредняющего НЧ фильтра. Размер маски определяет параметр n. Если n - двухкомпонентный вектор, то размер маски n(1)n(2). Если n - скаляр, то размер маски nn. Если при вызове функции параметр n опущен, то размер маски устанавливается равным 33.

Функция h=fspecial(‘unsharp’, a)возвращает маску h фильтра, повышающего резкость изображения. Размер маски 33. Параметрауправляет соотношением между центральным и граничными элементами маски. Данный параметр должен устанавливаться в диапазоне [0, 1]. По умолчаниюа=0.2.

Алгоритмы:

Усредняющий фильтр относится к фильтрам нижних частот. Он предназначен для фильтрации высокочастотного шума, и его работа сопровождается размытием изображения. Каждый элемент маски равен 1/MN, где М и N - размеры маски (количество строк и столбцов).

Фильтр Гаусса также относится к НЧ фильтрам. В отличие от усредняющего фильтра он в меньшей мере размывает обрабатываемое изображение [1]. Маска фильтра такова, что центральный элемент маски имеет наибольшее значение, он соответствует пику распределения Гаусса. Значения остальных элементов уменьшаются по мере удаления от центрального элемента. Уменьшение происходит в соответствии с распределением Гаусса. Маска формируется с использованием следующих соотношений:

;

,

где M и N - размеры маски; - среднеквадратическое отклонение распределения Гаусса.

Фильтр Лапласа относится к ВЧ фильтрам и предназначен для выделения границ (перепадов) во всех направлениях [1]. Маска фильтра конструируется следующим образом:

,

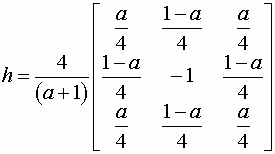где - параметр в диапазоне [0,1], передаваемый в функцию fspecial.

Лапласиан-гауссиан также относится к ВЧ фильтрам, но в отличие от фильтра Лапласа выделяет более резкие перепады. Маска фильтра создается по формуле

,

где M и N - размеры маски;

- среднеквадратическое отклонение распределения Гаусса.

Формула для вычисления выведена выше.

Маска фильтра, повышающего резкость изображения, создается следующим образом:

,

где - параметр в диапазоне [0,1], передаваемый в функцию fspecial.

Пример:

Рассмотрим, каким образом влияет среднеквадратическое отклонение распределения Гаусса на элементы маски фильтра Гаусса, возвращаемые функцией fspecial. Получим значения маски фильтра Гаусса размера 55 для среднеквадратического отклонения 0.5 и 0.7. На рис. 1а приведена частотная характеристика фильтра Гаусса с маской h05, а на рис. 1б- частотная характеристика фильтра Гаусса с маской h07.

%Пример демонстрирует формирование маски фильтра Гаусса %с помощью функции fspecial. %Создание маски для фильтра Гаусса размера 55 %и со среднеквадратическим отклонением 0.5. h05=fspecial(‘gaussian’, 5, 0.5) %Будет выведено: %h05 = % 0.0000 0.0000 0.0002 0.0000 0.0000 % 0.0000 0.0113 0.0837 0.0113 0.0000 % 0.0002 0.0837 0.6187 0.0837 0.0002 % 0.0000 0.0113 0.0837 0.0113 0.0000 % 0.0000 0.0000 0.0002 0.0000 0.0000 %Создание маски для фильтра Гаусса размера 55 %и со среднеквадратическим отклонением 0.7. h07=fspecial(‘gaussian’, 5, 0.7)%Будет выведено: %h07 = % 0.0001 0.0020 0.0055 0.0020 0.0001 % 0.0020 0.0422 0.1171 0.0422 0.0020 % 0.0055 0.1171 0.3248 0.1171 0.0055 % 0.0020 0.0422 0.1171 0.0422 0.0020 % 0.0001 0.0020 0.0055 0.0020 0.0001 %Вывод на экран частотных характеристики линейных фильтров %с масками h05 и h07.freqz2(h05, [32 32]); figure, freqz2(h07, [32 32]);

а)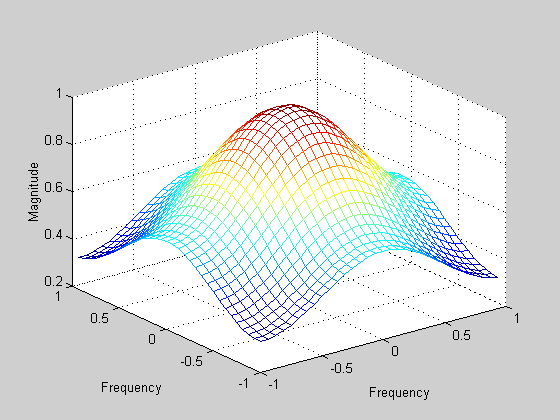

б) 

Двумерная линейная свертка

Синтаксис:

D=filter2(h, S) D=filter2(h, S, shape)

Описание:

Функция D=filter2(h, S)выполняет фильтрацию данных, заданных в двумерном массиве S, двумерным КИХ-фильтром, коэффициенты которого сведены в матрицу h, называемую также маской фильтра. Как правило, S и D являются полутоновыми изображениями. Результат фильтрации, возвращаемый в матрице D, вычисляется как двумерная свертка, выполняемая с помощью функцииconv2. Матрица D имеет тот же размер, что и S. Для этого при проведении вычислений исходная матрица временно дополняется необходимым количеством нулевых строк и столбцов.

Результат выполнения функции D=filter2(h, S, shape)зависит от значения параметра shape. Если параметру присвоено значение ‘same’, то в D возвращается центральная часть свертки, размер которой равен размеру исходных данных - S. Это параметр используется по умолчанию. Если параметру присвоено значение ’full’, возвращается весь результат свертки. При этом size(D)>size(S). Если параметру присвоено значение valid, возвращается только та часть свертки, при вычислении которой использовались краевые части исходных данных, дополненные нулями. При этом size(D)>size(S).

Результат D имеет формат представления данных double.

Алгоритм:

В функции filter2для выполнения двумерной свертки исходных данных с маской фильтра используется функцияconv2. Для передачи в функцию conv2 маска h поворачивается на 180⁰: conv2(S, rot90(h, 2), shape).

Сопутствующие функции: CONV2, FILTER,FSPECIAL,FTRANS2,FWIND1,FWIND2.

Адаптивная винеровская фильтрация

Синтаксис:

Id=wiener2(ls, [m n], noise) [Id, noise]=wiener2(ls, [m n])

Описание:

Функция Id=wiener2(Is, [m n], noise)формирует полутоновое изображение Id, которое является результатом адаптивной фильтрации Винера исходного полутонового изображения Is. Параметры m иn задают размеры скользящего окна, в пределах которого оцениваются среднее и среднеквадратичное отклонение значений яркости. Если при вызове функции параметры m и n опущены, то размер окна устанавливается равным 33.

Параметр noise устанавливает мощность гауссова белого шума, которым повреждено изображение. Этот параметр должен быть определен из каких–либо априорных сведений об изображении. Если это сделать не удается, то при вызове функцииwiener2параметр noise можно опустить. В этом случае мощность шума будет оцениваться автоматически.

Функция [Id, noise]=wiener2(Is, [m n])работает аналогично описанной выше и дополнительно возвращает оценку мощности гауссова белого шума.

Форматы представления данных исходного и результирующего изображений совпадают.

Алгоритм:

Функция wiener2использует алгоритм адаптивной винеровской фильтрации для подавления аддитивного гауссова белого шума. Данный алгоритм основан на статистических оценках фрагментов изображения в пределах скользящего окна размера nm пикселей [1, 2].

Для всех положений скользящего окна с центральным пикселем и координатами (r, с) вычисляются:

– средние значение яркости;

– дисперсия.

Данная формула применяется нерекурсивно для всех положений скользящего окна.

Если мощность гауссова белого шума не задана, то она оценивается как среднее из всех .

Обработка блоков изображения

Синтаксис:

D=blkproc(S, [m n], fun) D=blkproc(S, [m n], fun, P1, P2, …) D=blkproc(S, [m n], [mborder nborder], fun, …) D=blkproc(S, ‘indexed’, …)

Описание:

Функция D=blkproc(S, [m n], fun)формирует новое изображение D, пиксели которого являются результатом обработки функцией fun каждого из неперекрывающихся блоков размераисходного изображения S. Данная функция предназначена для обработки бинарных или полутоновых изображений. Исходное изображение S разбивается на неперекрывающиеся блокипикселей. Блоки располагаются вплотную друг к другу, начиная с левого верхнего угла изображения. При проведении вычислений исходное изображение временно дополняется столбцами нулей справа и строками нулей снизу так, чтобы размеры изображений были кратны соответствующим размерам блока. Например, на рис. 1 исходное изображение имеет 10 строк и 9 столбцов. Если для обработки использовать блок [3 4], то изображение дополняется двумя строками и тремя столбцами нулевых пикселей.

Рис. 1.

Существует 3 варианта задания параметра fun. Имя х является условным обозначением обрабатываемого блока изображения.

Параметр fun	Пример	Комментарий
Строка - имя функции	D=blkproc(S, [m n], ‘myfunc’);	Предварительно должна быть реализована функция myfunc, которая получает в качестве параметра блок х и возвращает матрицу или скаляр y: y=myfunc(x).
Строка - выражение языка	D=blkproc(S, [m n], ‘mean2(x)*ones(size(x))’);	В строку помещается выражение, допустимое синтаксисом MATLAB. Это выражение интерпретируется при выполнении каждого блока.
inline - функция	f=inline(‘std2(x)*ones(size(x))’); D=blkproc(S, [m n], f);	В качестве параметра функции inlineуказывается строка - выражение языка MATLAB. Оно компилируется и создается так называемая функция inline - функция, которая вызывается при обработке каждого блока. Использование inline - функций предпочтительнее по временным затратам.

В результате обработки каждого блока создается матрица, вектор или скаляр, из которых формируется результирующее изображение D. Таким образом, размеры исходного и результирующего изображения, как правило, различаются.

Функция D=blkproc(S, [m n], fun, P1, P2, …)формирует изображение D, передавая в функцию fun дополнительные параметры Р1, Р2 и т.д.

Функция D=blkproc(S, [m n], [mborder nborder], fun, …)формирует изображение D, пиксели которого являются результатом обработки функцией fun частично перекрывающихся блоков размераисходного изображения S. Каждый блок размерарасширяется вверх и вниз на mborder строк, а также вправо и влево на nborder столбцов. При этом центральные части размера(ядра) расширенных блоков не перекрываются друг с другом и располагаются, как и в предыдущем рассмотренном случае, последовательно начиная от левого верхнего угла изображения. В этом случае при проведении вычислений исходное изображение временно дополняется столбцами нулей справа и строками нулей снизу, чтобы размеры изображений были кратны соответствующим размерам блока, и дополнительно на mborder строк вверх и вниз и на nborder столбцов вправо и влево. Рис. 2 демонстрирует расположение двух соседних по диагонали блоков с размерами ядра 3х4 и mborder=1 nborder=2 на изображении, имеющем 10 строк и 9 столбцов. При вычислении изображение будет расширено на 3 строки вниз, 1 строку вверх, 5 столбцов вправо и 2 столбца влево.

Рис. 2.

Формат представления данных изображений S и D определяется реализацией функции fun.

Функция D=blkproc(S, ‘indexed’, …)аналогична рассмотренным выше, но предназначена для обработки палитровых изображений. При проведении вычислений исходное изображение временно дополняется либо единицами при формате представления данных Xs-double, либо нулями при формате представления данных Xs-uint8.

Повысить эффективность обработки блоков можно с помощью функции colfilt, которая предварительно преобразует блоки в столбцы.

Пример:

Рассмотрим выравнивание фона изображения с использованием функции blkproc. Неравномерный фон является серьезным дефектом изображений, который ухудшает визуальное восприятие и мешает выделению объектов с помощью порогового ограничения.

Исходное биомедицинское изображение показано на рис. 3,а. Это изображение характеризуется значительной неравномерностью фона. С помощью функцииblkprocоценим яркость фона как среднее значение яркостей пикселей в блоках 25х25 пикселей. В результате работы blkproc получается изображение с размером в 25 раз меньшим, чем исходное. Для того чтобы изображение фона и исходное изображение были одинакового размера, изображение фона увеличивается с помощью функцииimresize. Полученная оценка фона показана на рис. 3,б.

Если вычесть изображение фона из исходного изображения, то получится изображение с равномерным фоном. Добавление константы 0.5 необходимо для того, чтобы значения пикселей получившегося изображения были в диапазоне [0, 1]. Функцией imadjastрезультирующее изображение дополнительно контрастируется. Получившийся результат показан на рис. 3,в.

%Пример демонстрирует выравнивание фона. %Чтение изображения. I=imresd(‘image03.tif’); I=im2double(I); %Вывод на экран. imshow(I); %Получение оценки фона изображения как среднего %в блоках 25х25 пикселей. F=inline(‘mean2(x)’); fon=blkproc(I, [25 25],f); fon=imresize(fon, size(I), ‘bicubic’); figure, imshow(fon); %Вычитаем фон и контрастируем получившееся изображение. I=I-fon+0.5; I=imadjust(I, [0.2 0.7], 1); % Вывод на экран результата. figure, imshow(I);

а)

б)

в)

Рис. 3.

Сопутствующие функции:BESTBLK,COLFILT.

б) 

Рис. 1.

Сопутствующие функции: FILTER2,CONV2,EDGE.

Выделение границ

Синтаксис:

BW=edge(l, method) BW=edge(l, method, thresh) BW=edge(l, method, thresh, P) [BW, thresh]=edge(l, method, ...)

Описание:

Для сегментации на изображениях часто необходимо обнаружить границы объектов - участки изображения, в которых есть перепад яркости.

Функция BW=edge(I, method)предназначена для выделения границ на исходном полутоновом изображении I. Данная функция возвращает бинарное изображение BW такого же размера, как исходное I. Пиксель BW(r, с) равен 1, если пиксель I(r, с) принадлежит границе. Для обнаружения границ может использоваться несколько методов. Применяемый метод задается в параметре method в виде одной из следующих строк: 'sobel', 'prewitt', 'roberts', 'log', 'zerocross', 'canny'. Если параметр method при вызове функции опущен, то по умолчанию он полагается равным 'sobel'.

Для каждого из методов определения границ можно задать дополнительные параметры. Для этого используется одна из функций BW=edge(I, method, thresh), BW=edge(I, method, thresh, P),где параметр thresh задает порог для определения того, принадлежит ли пиксель к границе, а в параметре Р передаются настройки, специфичные для каждого из методов.

Если при вызове функции параметр threshопущен, то значение порога выбирается автоматически. Получить значение порога можно, дополнительно определив выходной параметр thresh: [BW, thresh]=edge(I, method,...).

Рассмотрим использование функции edgeдля каждого из методов выделения границ.

Функция BW=edge(I, 'sobel', thresh)для определения границ использует фильтрацию исходного изображения I фильтром Собеля [1, 3]; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh. Для данного метода можно указать дополнительный параметр direction: BW=edge(I, 'sobel', thresh, direction), который определяет, какие границы будут обнаруживаться. Параметр direction может принимать значения:

'horizontal' - выделение горизонтальных границ;

'vertical' - выделение вертикальных границ;

'both' - выделение границ во всех направлениях (данное значение используется по умолчанию, когда параметр direction не определен).

Функция BW=edge(I, 'prewitt', thresh)для определения границ использует фильтрацию исходного изображения I фильтром Превита [1,3]; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh. Для данного метода можно указать дополнительный параметр direction: BW=edge(I, 'prewitt', thresh, direction), который определяет, какие границы будут обнаруживаться. Возможные значения параметра direction описаны выше.

Функция BW=edge(I, 'roberts', thresh)для определения границ использует фильтрацию исходного изображения I фильтром Робертса; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh.

Функция BW=edge(I, 'log', thresh)для определения границ использует фильтрацию исходного изображения I фильтром лапласиан–гауссиана [1, 2]; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh. Для формирования маски фильтра используется функцияfspecialс параметрами sigma=2 (среднеквадратичное отклонение) и n=ceil(sigma*3)*2+1 (размер маски). Параметр sigma можно задать в параметре функцииedge: BW=edge(I, 'log', thresh, sigma).

Функция BW=edge(I, 'zerocross', thresh, h)для определения границ использует фильтрацию исходного изображения I линейным фильтром с маской h; пиксель считается относящимся к границе, если соответствующий ему пиксель результата фильтрации имеет значение, большее thresh.

Функция BW=edge(I, 'canny', thresh)использует для определения границ метод Канни. Это достаточно сложный метод, состоящий из большого числа этапов [4]. Суть метода состоит в поиске локальных участков с перепадами яркости. Перепады яркости ищутся с помощью фильтрации по каждой из осей одномерным фильтром лапласиан–гауссиана (см. функциюfspecial). В методе Канни для классификации перепадов на "слабые" и "сильные" используется два порога - нижний и верхний. "Слабые" границы отмечаются в результирующем изображении, только если они соединены с "сильными". Для зашумленных изображений данный метод обеспечивает наилучшее обнаружение границ по сравнению с остальными методами функцииedge, но требует существенно большего времени.

Параметр thresh может являться двухэлементным вектором. В этом случае первый элемент вектора задает значение нижнего порога, а второй элемент - значение верхнего порога. Если параметр thresh является скалярным значением, то thresh задает значение верхнего порога, а для нижнего порога используется значение 0.4*thresh. Если параметр thresh при вызове функции опущен или в качестве thresh передан пустой массив ([ ]), то значения порогов определяются автоматически.

В функцию BW=edge(I, 'canny', thresh, sigma)дополнительно передается параметр sigma, задающий среднеквадратичное отклонение распределения Гаусса, которое используется при формировании маски фильтра, выделяющего перепады яркости.

Пример:

Рассмотрим выделение границ методом Собеля. Исходное изображение показано на рис. 1,а. Результирующее изображение, на котором отмечены границы, показано на рис. 1,б.

% Пример демонстрирует выделение границ методом Собеля. % Чтение исходного изображения и вывод его на экран. I=imread(‘lena.bmp’); imshow(l); % Выделение границ методом Собеля и вывод результата на экран. BW=edge(l, ‘sobel^’, 0.09); figure, imshow(BW);

а) б) Рис. 1.

Сопутствующие функции: FILTER2,FSPECIAL.

26