1. Абстрактные автоматы

Определение. Абстрактным автоматом Милиназывается преобразователь, представимый пятёркой

S=<Z,W,A,,>,

где Z– входной алфавит {z1,z2, …,zr},

W– выходной алфавит {w1,w2,…,wp},

A – алфавит состояний {a1,a2,…,at},

– функция переходов AxZА,

 – функция выходов AxZW.

Если, кроме того, определено начальное состояние автомата a₀(a₀– символ изА), то говорят обинициальном автомате Мили.

Семантика: автомат функционирует в дискретном времени. В лю-бой момент времени он находится в некотором состоянииa_iиз множест-ваA, и на его вход поступает входной сигналz_iиз множестваZ. В зави-симости от состояния и входного сигнала в следующий момент автомат переходит в новое состояниеa_j, определяемое функцией перехода,a_j=(a_i,z_i), при этом на его выходе формируется выходной сигналw=(a_i,z_i) (рис.1.1). В инициальном автомате в начале функционирова-ния автомат находится в состоянииa₀.

Автомат МилиPпредставляется матрицей переходов и матрицей выходов, описывающими соответствующие функции.

Пример 1. Автомат задан на множествах входовZ={z1,z2,z3}, состоянийA={a1,a2,a3,a4,a5,a6} и выходовW={w1,w2}. Его функционирование описывается матрицами переходов и выходов, приведёнными в табл.1.1 и 1.2.

Таблица 1.1

Таблица 1.2

a1

a2

a3

a4

a5

a6

a1

a2

a3

a4

a5

a6

z1

a3

a5

a6

a6

a1

a5

z1

w1

w1

w2

w1

w2

w1

z2

a1

a6

a4

a4

a4

a1

z2

w1

w1

w1

w1

w1

w1

z3

a5

a1

a3

a2

a5

a3

z3

w1

w1

w2

w2

w2

w1

Автомат Мили может быть также представлен в виде объединённой матрицы. В этом случае каждая клетка матрицы состоит из двух частей, в одной из которых записывается следующее состояние (функция (ai,z)), во второй части – выход (функция(ai,z)).

Таблица 1.3
	a1	a2	a3	a4	a5	a6
z1	a3w1	a5w1	a6w2	a6w1	a1w2	a5w1
z2	a1w1	a6w1	a4w1	a4w1	a4w1	a1w1
z3	a5w1	a1w1	a3w2	a2w2	a5w2	a3w1

Объединённая матрица представленного выше автомата показана в табл. 1.3.

Автомат Мили может быть описан в виде графа. Вершинам этого графа сопоставлены состояния, дугам – переходы. При этом на каждой дуге записывается значение входа, определяющего этот переход, и значение выхода на этом переходе. Эта пара вход-выход называется весом дуги. Для рассмотренного автомата граф имеет вид как на рис.1.2

Рис.1.2

Автоматом Мураназывают автомат, в котором функция выходов зависит только от состояния, то есть для него функция выходов автомата::AW.

Пример2. Автомат Мура задан на тех же множествах, что и автомат в примере 1, а его функционирование описывает табл. 1.4.

В графе автомата Мура дуги взвешиваются только значением соответствующего входа, значение выходов приписываются его вершинам.

Таблица 1.4
	w a1	w1 a2	w2 a3	w1 a4	w2 a5	w1 a6
z1	a3	a5	a6	a6	a1	a5
z2	a1	a6	a4	a4	a4	a1
z3	a5	a1	a3	a2	a5	a3

Для приведённого автомата граф будет иметь вид как на рис.1.3

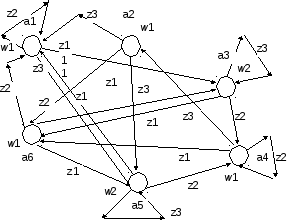
Рис.1.3

Реакция автомата в состоянии aiна входное словоz* определяется по таблицам переходов и выходов. Для последнего примера реакцией автомата в состоянииa2 на словоz1z2z1 будет словоw2w1w1.