2.2.2. Задача размещения

Задача размещения заключается в том, чтобы на основе принципиальной схемы устройства и информации об упаковке элементов по блокам разместить эти элементы в блоке (например, на печатной плате) наилучшим образом.

Элементы могут размещаться как на одной, так и на обеих сторонах печатной платы. Размещение может быть оптимизировано по таким параметрам как

• плотность заполнения платы,

• суммарная длина связей между элементами, и др..

Алгоритмы размещения компонентов на плате в целом аналогичны алгоритмам компоновки. Точно также основными алгоритмами размещения являются:

• последовательный алгоритм

• итерационный алгоритм

Последовательный алгоритм

Сначала размещаются элементы, для которых положение на плате известно заранее (например, разъемы), или элементы с максимальным количеством связей с другими. Далее, элементы последовательно размещаются на плате таким образом, чтобы суммарная длина связей с уже размещенными элементами была минимальной.

Метод обладает тем же недостатком, что и последовательный метод компоновки.

Итерационный алгоритм

Итерационный алгоритм помогает оптимизировать начальное размещение элементов, путем перестановки мест некоторых элементов, и оценки полученного результата. Мы использовали такую модель: пусть как-то элементы размещены. Зафиксируем первый и третий уровни (первый уровень – это фиксированный разъём). Представим, что элементы второго уровня располагаются на условном «стержне», а связям соответствуют натянутые резинки или пружинки. Отпустим элементы второго уровня, под действием пружинок они займут положения, которые будут соответствовать минимуму натяжений. Зафиксируем это положение, и перейдем к определению расположения на третьем уровне, закрепив еще и элементы четвертого уровня. Для такой модели составлены соответствующие математические уравнения, решая которые получим некоторое локальное распределение элементов.

2.2.3. Задачи трассировки

Задачей трассировки является прокладка на печатной плате соединений между элементами. При трассировке учитывается стоимость прокладки проводников по каждому направлению, стоимость сверления переходных отверстий, минимизируется число изгибов проводников, а также ряд других параметров.

Алгоритмы трассировки:

• Волновой

• Лучевой

• Канальный

• Магистральный

Волновой алгоритм Ли

Волновой алгоритм Ли имитирует распространение сигнала в среде. Источником сигнала является одна из точек, между которыми прокладывается соединение. Все соседние с ней точки также становятся источниками волны следующего уровня. И так продолжается до тех пор, пока волна не дойдет до нужной точки.

После этого точки соединяются в обратном порядке:

16 – 15 – 14 - … - 0.

Ускорить процесс можно, если пустить волну одновременно из обеих точек навстречу друг другу.

На рис. показан результат трассировки по алгоритму Ли. Здесь затемненными прямоугольниками выделены зоны запрета, где трассы проводить нельзя, цифрами указаны шаги выполнения алгоритма.

Магистральный алгоритм

В магистральном алгоритме трассировки соединение строится следующим образом: начинаем движение из одной точки и делаем шаг в некотором направлении (горизонтальном или вертикальном), пытаясь приблизиться к нужной точке. Если на пути встречается препятствие – возвращаемся на шаг меняем направление.

М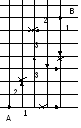ожно также двигаться навстречу из обеих точек до пересечения магистралей.

Рисунок 5

Канальный алгоритм

Канальный алгоритм трассировки предполагает размещение всех связей между элементами в канале связи.

Таким образом, задача трассировки сводится к задаче укладки отрезков по каналу.

Рисунок 6