
ФХНМ часть3 / Rempel ФХНМ-Л44
.pdfФизико-химия наноструктурированных материалов
Лекция 4.4. Дифракционные методы для
определения областей когерентного рассеяния и микродеформаций
Дифракция рентгеновских лучей, электронов и тепловых нейтронов на наноструктурированных материалах. Выбор оптимального метода дифракции для исследования атомной структуры наноматериалов. Понятия областей когерентного рассеяния, механических напряжений и микродеформаций. Уширение дифракционных линий с учетом инструментальной функции или функции разрешения прибора. Определение размера частиц по формуле Шеррера. Построение графика зависимости уширения линий от величины вектора рассеяния. Определение размеров областей когерентного рассеяния и микродеформаций по методу Вильямсона-Холла.
Профессор Ремпель А.А., член-корреспондент РАН, ИХТТ УрО РАН

Формула Шеррера для определения размеров областей
когерентного рассеяния рентгеновского излучения
D
Области когерентного рассеяния
 размер частицы
размер частицы

Статья Патерсона о формуле Шеррера
В статье приводится точный вывод формулы для частицы сферической формы. Особое внимание уделяется различным значениям коэффициента K, зависящим от способа описания дифракционного пика.
Scherrer P. Bestimmung der Grosse und der Inneren Struktur von Kolloidteilchen mittels Röntgenstrahlen // Nachrichten Gesellschaft Wissenschaft Gottingen, Math.-Phys. Kl. 2
(1918) 98-100
Вывод формулы выполнен позднее для частицы с формой элементарной ячейки Н. Селяковым Seljakow N. Eine röntgenographische Methode zur Messung der absoluten Dimension einzelner Kristalle in Körpern von fein-kristallischem Bau //
Zeitschrift für Physik Bd.31 No 516 (1925) 439-444

Схема съемки рентгенодифракционного спектра по
методу Брэгга-Брентано
1 – источник рентгеновского монохроматического излучения;
2 – поликристалл или порошок исследуемого вещества;
3 – кювета или держатель образца;
4 – детектор;
5, 6 – два круга, по которым в противоположных направлениях вращаются источник рентгеновского излучения и детектор;
- угол скольжения; 2 - угол рассеяния

Дифракция рентгеновских лучей на наноструктурированных материалах
Съемка в режиме Брэгга-Брентано ω-2θ
Исследование структуры порошка
10° < 2θ < 125°
|
|
Дифрактометр рентгеновский Philips X’Pert |
||
Источник |
|
|
|
|
рентгеновского |
|
|
|
|
излучения |
|
|
|
|
Cu Kα1,α2 |
|
|
|
Детектор |
|
|
|
|
|
U = 40 kV |
|
|
|
X’Celerator |
I = 35 mA |
|
|
|
|
Щель |
|
|
|
Щель |
вертикальная |
|
|
|
|
|
|
горизонтальная |
||
0.04 |
|
|
||
|
|
Щель |
¼° |
|
горизонтальная |
|
|||
¼° |
Щель |
|
вертикальная |
|
горизонтальная |
Образец |
0.04 рад |
|
|
½°

Экспериментальные рентгенодифракционные спектры нанокристаллического вещества и стандартного порошка в зависимости от угла рассеяния 2θ
Интенсивность рассеяния, усл. ед.
CuK 1,2
кристаллический LaB6
нанокристаллический PbS
20 |
30 |
40 |
50 |
60 |
70 |
80 |
2, град.

Рентгеноструктурный анализ: уширение пика, параметры уширения
Два различных параметра FWHM и IB, которые
описывают уширения пиков, учитывая их профиль
FWHM (full width at half maximum, полная ширина на половине высоты) – это разность между двумя крайними значениями независимой переменной, при которых зависимая переменная равна половине ее максимального значения.
Другими словами, это полная ширина пика на половине его высоты.
IB (integral breadth, интегральная ширина)
– это значение, равное отношению площади под кривой к максимальному значению функции.
Другими словами, IB – это ширина прямоугольника, высота которого равна максимальному значению функции, а площадь прямоугольника равна площади под кривой.
IB
Sпика= Sпрямоугольника

Две основные функции для описания профиля дифракционных пиков
Функция Гаусса
g( ) hG exp[ ( 0 )2 /(2G2 )]
IBG g( )d / hG 
 2 G 2.507 G
2 G 2.507 G
FWHMG 2
 2 ln 2 G 2.355 G
2 ln 2 G 2.355 G
Функция Коши-Лоренца
l( ) h |
1 ( |
|
) |
|
/ |
|
1 |
|
2 |
2 |
|
||||
|
|
|
|
|
|
||
L |
|
0 |
|
|
|
L |
|
IBL l( )d / hL π L
FWHML=2θL
θG =0,105 R=0.9698
θG =0,83 R=0.9293
Подгонка (аппроксимация) методом наименьших квадратов

Рентгеноструктурный анализ: уширение пика – функция псевдо-Фойгта
Функция псевдо-Фойгта – это взвешенная сумма функций Гаусса и Лоренца
V ( ) c l( ) (1 c) g( )
|
|
( 0 )2 1 |
|
( 0 )2 |
||
V ( ) ca 1 |
|
|
|
(1 c)a exp |
|
|
2 |
2 |
|||||
|
|
L |
|
|
2 G |
|
b =θ G= θL
с – коэффициент, учитывающий относительный вклад от функций Гаусса и Лоренца
b=0,098 c=0,209 R=0.9727
IB |
V |
I |
V |
( ) / a cIB |
L |
(1 c)IB |
G |
c(1 |
2 / )IB |
L |
IB |
G |
(0.635 c 2.507)b |
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|||||||||||||
FWHMV c FWHML (1 c) FWHMG |
2b(c (1 c) 2ln 2) ~1% |
|||||||||||||||
FWHMV b (2.355 0.276 c 0.079 c2 ) |
~0.1% |
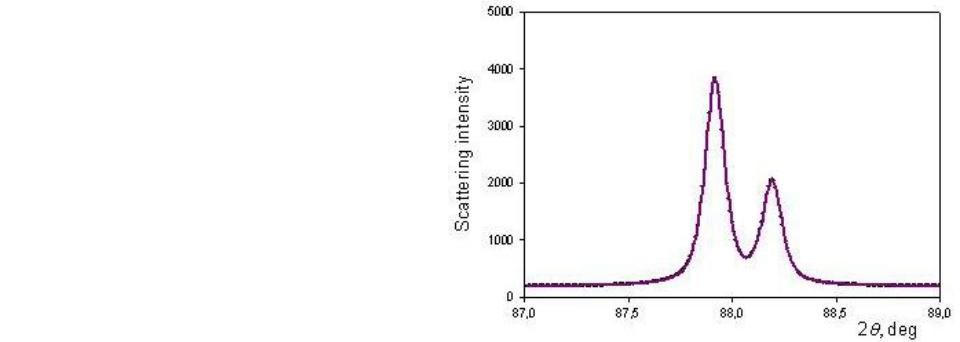
Рентгеноструктурный анализ: уширение пика – дублет
Рентгеновское излучение от медного источника имеет два монохроматических вклада:
CuK 1 с длиной волны λ1 = 0.154056 нм,
и
CuK 2 с длиной волны λ2 = 0.154439 нм.
Вот почему пики кристаллических веществ расщепляются на дублет!
2
Профиль дублета описывается суперпозицией двух функций псевдо-Фойгта, |
|||||
позиции максимумов 0,1 и 0,2 которых связаны уравнением: |
|||||
|
2arcsin (λ |
/ λ )sin(2 |
|
/ 2) |
CuKα1 |
0,2 |
2 |
1 |
0,1 |
|
|
|
|
||||
Интенсивность CuK 2-пика в |
|
дублете составляет 0.497 от |
CuKα2 |
интенсивности CuK 1-пика. |
I(θ)=I0+V1(θ, θ0,1)+0.497·V2(θ,
θ0,1)
