
- •Министерство образования и науки Российской Федерации
- •Основы теории управления
- •230100 - Информатика и вычислительная техника, 230101 - Вычислительные машины, комплексы, системы и сети, 230102 - Автоматизированные системы обработки информации и управления
- •Методические рекомендации
- •Экзаменационные вопросы Дисциплина: Основы теории управления
- •Приложение. Вид экзаменационного билета
|
|
|
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
ГОУ ВПО «Уральский государственный технический университет - УПИ»

 Кафедра
Автоматики и
Информационных
Технологий
Кафедра
Автоматики и
Информационных
Технологий
Основы теории управления
Вопросы и задачи для проведения итоговой аттестации
для студентов направлений и специальностей подготовки:
230100 - Информатика и вычислительная техника, 230101 - Вычислительные машины, комплексы, системы и сети, 230102 - Автоматизированные системы обработки информации и управления

Екатеринбург УГТУ – УПИ 2007
УДК 62-50
Составители: Л.А.Ванеева, Е.Э.Страшинин, А.В.Цветков
ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ: Вопросы и задачи для проведения итоговой аттестации / Ванеева Л.А., Страшинин Е.Э., Цветков А.В. Екатеринбург: УГТУ - УПИ, 2007. 15 с.
Приведены вопросы и задачи для проведения итоговой аттестации по дисциплине «Основы теории управления» в виде письменного экзамена. Все вопросы и задачи оценены в баллах от одного до трех в соответствии с их сложностью. В билет включается 6 позиций из разных разделов с общей суммой баллов 11.
Приведены рекомендации по проведению экзамена.
Библиогр.: 8 назв.
Подготовлено кафедрой “Автоматика и информационные технологии”
Ó Уральский государственный технический университет - УПИ, 2007
СОДЕРЖАНИЕ
МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ 4
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ 4
ПРИЛОЖЕНИЕ. Вид экзаменационного билета 16
Методические рекомендации
Изучение раздела дисциплины «Основы теории управления» предусматривает итоговую аттестацию в виде экзамена. Для повышения объективности экзамен проводится в письменном виде.
Все экзаменационные вопросы имеют трудность, оцененную в баллах от 1 до 3. В билет включается 6 вопросов: 2 со сложностью 1 балл, 3 со сложностью 2 балла и 1 со сложностью 3 балла. Вопросы каждого билета охватывают основные разделы дисциплины.
На экзамен отводится 2 астрономических часа. Студенты могут отвечать на вопросы в произвольном порядке. На экзамене разрешается пользоваться справочной литературой по преобразованию Лапласа и Z-преобразованию, отчетами по лабораторным работам.
При проверке преподаватель оценивает ответы студента и выставляет баллы в соответствии с принятой шкалой. Допускается дробление баллов с дискретностью 0.5. Оценка определяется делением суммы набранных баллов пополам и округлением по правилам арифметики. Таким образом, оценка отлично выставляется при сумме баллов не менее 9, удовлетворительно не менее 5.
После проверки и выдачи результатов студентам для ознакомления, отклонения или принятия возможных апелляций оценки выставляются в экзаменационную ведомость и зачетные книжки.
Экзаменационные вопросы Дисциплина: Основы теории управления
-
Перечислите и приведите функциональные схемы, характеризующие основные принципы управления. (1 балл).
-
Перечислите и приведите типовые передаточные функции систем автоматического управления. (1 балл).
-
Перечислите и приведите передаточные функции не менее пяти типовых звеньев систем автоматического управления. (1 балл).
-
Перечислите и приведите графики, характеризующие основные алгоритмы функционирования систем автоматического управления. (1 балл).
-
Динамическое звено описывается уравнением
![]()
Построить
для него логарифмические частотные
характеристики и привести вид
амплитудно-фазовой характеристики.
Записать выражение сигнала на выходе
в установившемся режиме, если входной
сигнал
![]() (2 балла).
(2 балла).
-
На вход линейной электрической цепи подается сигнал в виде одиночного прямоугольного импульса амплитудой 1 В и длительностью 1 сек. Определите выходной сигнал u2(t) и постройте его график, если R=1 МОм, С=1 мкФ (2 балла).

-
На вход линейной электрической цепи подается гармонический сигнал
 .
Какой вид и какие значения параметров
будет иметь выходной сигнал u2(t)
после окончания переходных процессов
(постройте его график), если Um
=10 В,
=1 c-1,
R=1 МОм, С=1 мкФ (2 балла).
.
Какой вид и какие значения параметров
будет иметь выходной сигнал u2(t)
после окончания переходных процессов
(постройте его график), если Um
=10 В,
=1 c-1,
R=1 МОм, С=1 мкФ (2 балла).

-
На вход электрической цепи подается гармонический сигнал
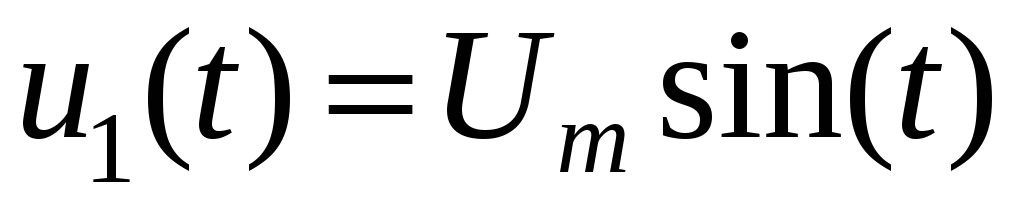 .
Какой вид и какие значения параметров
будет иметь выходной сигнал u2(t)
после окончания переходных процессов,
если Um
=10 В,
=0.1 c-1,
R=1 МОм, С=1 мкФ (2 балла).
.
Какой вид и какие значения параметров
будет иметь выходной сигнал u2(t)
после окончания переходных процессов,
если Um
=10 В,
=0.1 c-1,
R=1 МОм, С=1 мкФ (2 балла).

-
Для цепи

составить
векторно-матричное описание и вычислить
передаточную функцию от входа u(t) к
выходу uс(t)
при следующих значениях параметров:
L=0.1 Гн, C=0.001 Ф, R=2 Ом. Построить логарифмические
частотные характеристики и определить
амплитуду установившегося гармонического
сигнала на выходе, если на вход подается
![]() (2 балла).
(2 балла).
-
Для цепи

составить
векторно-матричное описание и вычислить
передаточную функцию от входа u(t) к
выходу uс(t)
при следующих значениях параметров:
L=0.1 Гн, C=0.001 Ф, R=2 Ом. Построить логарифмические
частотные характеристики и определить
амплитуду установившегося гармонического
сигнала на выходе, если на вход подается
![]() .
(2 балла).
.
(2 балла).
-
Оцените устойчивость замкнутой системы по критерию Найквиста, если передаточная функция разомкнутой системы:
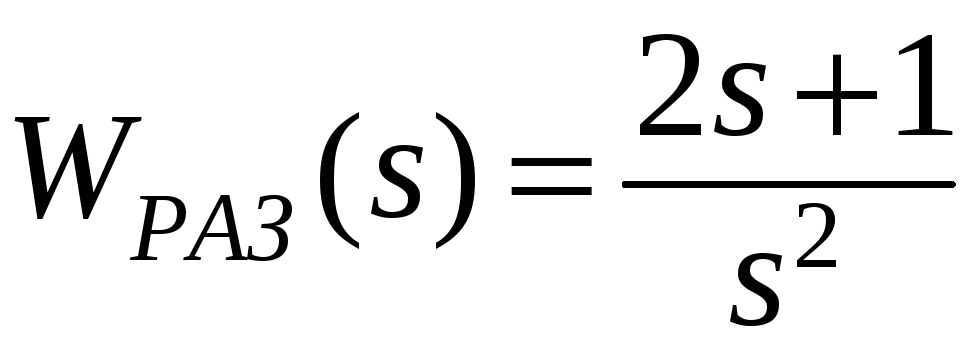 .
Приведите качественный вид АФХ,
определите количество правых корней
(2 балла).
.
Приведите качественный вид АФХ,
определите количество правых корней
(2 балла). -
Для электрической цепи

составить линеаризованную модель для вычисления отклонения выходного напряжения ∆u2 в зависимости от ∆u1 и ∆R1 . Номинальные значения: u10 =10 В, R10=R20=10 кОм. Представьте в виде структурной схемы связь приращений указанных входных переменных и выходной переменной. (2 балла).
-
Для системы, имеющей следующее расположение нулей и полюсов определить переходную функцию с точностью до коэффициента передачи и привести ее качественный вид (2 балла).
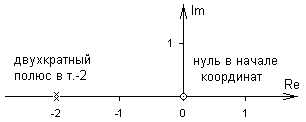
-
Для электрической цепи

составить линеаризованную модель для вычисления отклонения выходного напряжения ∆u2 в зависимости от ∆u1 и ∆R2 . Номинальные значения: u10 =10 В, R10=R20=10 кОм. Представьте в виде структурной схемы связь приращений указанных входных переменных и выходной переменной. (2 балла).
-
Для системы с передаточной функцией

оцените с использованием метода корневого годографа, как будут меняться ее свойства при введении отрицательной обратной связи и изменении коэффициента обратной связи (3 балла).
-
Для стабилизации неустойчивого маятника введена обратная связь по положению (углу). Используя метод корневого годографа определите (если возможно) значения коэффициента обратной связи, при котором в данной замкнутой системе будут затухающие процессы. Используйте линеаризованную модель маятника
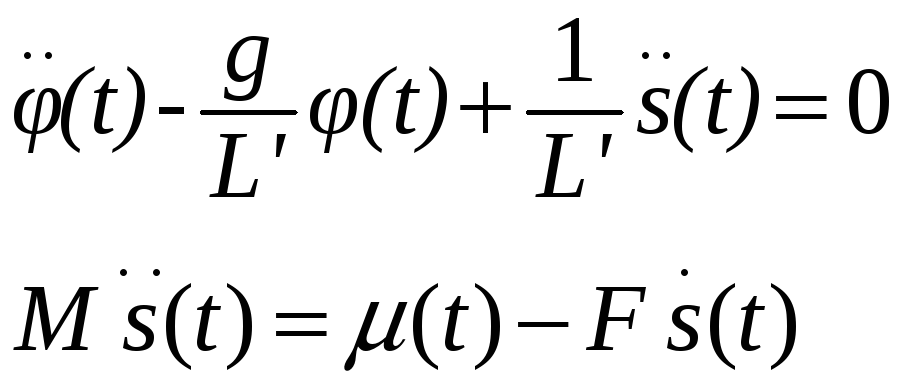
при следующих значениях параметров:
![]() c-1,
c-1,
![]() c-2,
c-2,
![]() Кг-1,
L'=0.84
м, g=9.81
м/с2.
(3 балла)
Кг-1,
L'=0.84
м, g=9.81
м/с2.
(3 балла)
-
Задана система
 ,
где
,
где
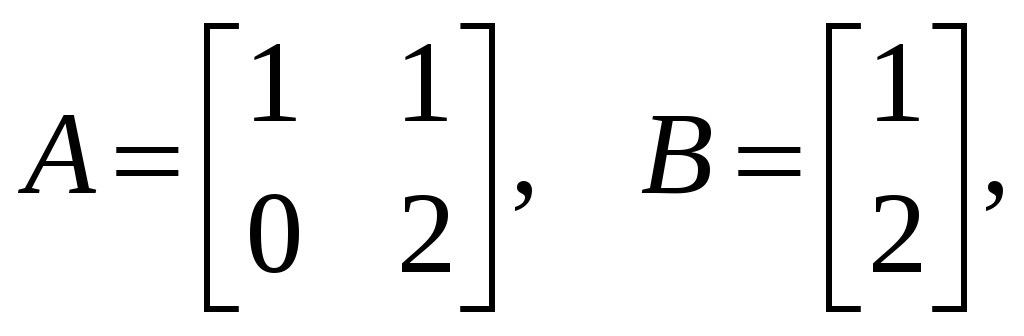
Рассчитать
вектор обратной связи L для управления
в виде обратной связи по состоянию
![]() ,
чтобы замкнутая система была генератором
гармонических колебаний с частотой =2
рад/сек. (3 балла).
,
чтобы замкнутая система была генератором
гармонических колебаний с частотой =2
рад/сек. (3 балла).
-
Для объекта управления с передаточной функцией
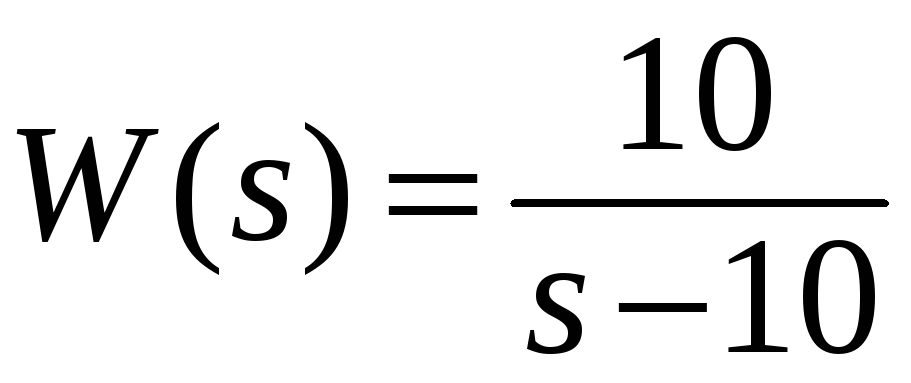 оцените, используя метод корневого
годографа, возможность обеспечить в
замкнутой системе полюсы передаточной
функции, равные
оцените, используя метод корневого
годографа, возможность обеспечить в
замкнутой системе полюсы передаточной
функции, равные
 и
и
 c помощью пропорциональной обратной
связи. В случае невозможности определите
необходимое корректирующее звено и
его параметры (3 балла).
c помощью пропорциональной обратной
связи. В случае невозможности определите
необходимое корректирующее звено и
его параметры (3 балла). -
Линейная система описывается дифференциальным уравнением
![]()
Определите
параметры выходного сигнала после
окончания переходного процесса, если
входной сигнал
![]() (2 балла).
(2 балла).
-
С помощью алгебраического критерия оцените устойчивость замкнутой системы и определите критическое значение коэффициента передачи, если передаточная функция разомкнутой имеет вид:
![]() (2
балла).
(2
балла).
-
Для объекта управления с передаточной функцией
 рассчитать обратную связь и коэффициент
при внешнем воздействии, обеспечивающие
длительность переходного процесса не
более 0.6 сек и установившееся значение
на выходе, равное 1 (2 балла).
рассчитать обратную связь и коэффициент
при внешнем воздействии, обеспечивающие
длительность переходного процесса не
более 0.6 сек и установившееся значение
на выходе, равное 1 (2 балла). -
Для объекта управления с передаточной функцией
 рассчитать обратную связь и коэффициент
при внешнем воздействии, обеспечивающие
длительность переходного процесса не
более 0.6 сек и установившееся значение
на выходе, равное 1. (2 балла).
рассчитать обратную связь и коэффициент
при внешнем воздействии, обеспечивающие
длительность переходного процесса не
более 0.6 сек и установившееся значение
на выходе, равное 1. (2 балла). -
Задана система
 ,
где
,
где

Рассчитать
вектор обратной связи L для управления
в виде обратной связи по состоянию
![]() ,
чтобы замкнутая система была генератором
гармонических колебаний с частотой
= 2 рад/сек. (3 балла).
,
чтобы замкнутая система была генератором
гармонических колебаний с частотой
= 2 рад/сек. (3 балла).
-
Для объекта управления с передаточной функцией разомкнутой системы
![]()
определить область устойчивости замкнутой системы по коэффициенту k.(2 балла).
-
По виду логарифмических частотных характеристик запишите выражение передаточной функции и приведите вид АФХ. (1 балл).

-
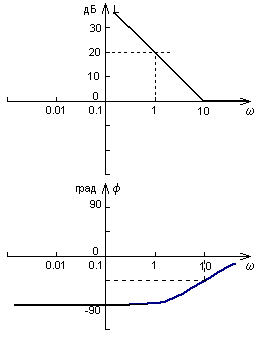
По виду логарифмических частотных характеристик запишите выражение передаточной функции и приведите вид АФХ(1 балл).
-
По виду логарифмических частотных характеристик запишите выражение передаточной функции и приведите вид АФХ. (1 балл).

-
По виду логарифмических частотных характеристик запишите выражение передаточной функции и приведите вид АФХ (1 балл).

-
По виду логарифмических частотных характеристик запишите выражение передаточной функции и приведите вид АФХ (1 балл)

-
Для объекта управления с передаточной функцией
![]()
используя метод корневого годографа, оцените характер процессов в замкнутой системе при различных значениях коэффициента k (3 балла).
-
Оцените устойчивость системы, имеющей следующую структурную схему:
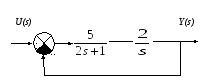
Определите сигнал y(t), если на вход системы подать единичный ступенчатый сигнал (2 балла).
-
Линейная система задана в виде структурной схемы:
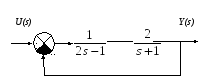
Оцените устойчивость разомкнутой и замкнутой систем (2 балла).
-
Оцените устойчивость a) разомкнутой, и б) замкнутой импульсной системы при:
а) T0=1 сек. и б) T0 =0.1 сек.(3 балла):

-
Определите и изобразите реакцию замкнутой системы на входное воздействие
 (1 балл).
(1 балл).

-
На вход электрической цепи подается сигнал
 .
Определите выходной сигнал u2(t)
и постройте его график, если R1=1
КОм, R2=1
КОм, C=1 мкФ.(2 балла).
.
Определите выходной сигнал u2(t)
и постройте его график, если R1=1
КОм, R2=1
КОм, C=1 мкФ.(2 балла).

-
Линейная система задана в виде следующей структурной схемы:

Определите величину ошибки стабилизации при действии единичного ступенчатого сигнала. (2 балла).
-
Линейная система задана в виде следующей структурной схемы:

Оцените устойчивость данной системы и приведите качественный вид процессов при действии на входе единичного ступенчатого сигнала.(2 балла).
-
Определите величину статической ошибки в системах при входном воздействии
 .
(2 балла).
.
(2 балла).
a)
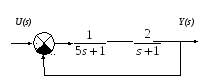
б)

-
Определите частотные свойства электрической цепи. Приведите график амплитудно-фазовой частотной характеристики, если R1=R2=10 Ком, С=1 мкФ. (2 балла).

-
Оценить устойчивость разомкнутой и замкнутой импульсной системы при T0=1 сек. Формирующее звено - фиксатор нулевого порядка. Определить переходную функцию замкнутой системы(3 балла).

-
Определить и изобразить реакцию непрерывной части импульсной системы на единичный импульс, T0=1 сек. Формирующее звено - фиксатор нулевого порядка (2 балла).

-
Для заданной структурной схемы приведите названия, выражения и укажите входные и выходные переменные типовых передаточных функций: (2 балла).

-
По передаточной функции дискретного корректирующего звена W(z) составьте разностное уравнение для расчета выходного сигнала: (2 балла).
 .
.
-
Динамическое звено описывается уравнением:

Построить
для него логарифмические частотные
характеристики и привести вид
амплитудно-фазовой характеристики.
Записать выражение сигнала в установившемся
режиме, если входной сигнал
![]() ,
,
![]() .
(2 балла).
.
(2 балла).
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
-
Юревич Е.И. Теория автоматического управления: Учебник для вузов. СПб.: БХВ-Петербург, 2007. 560 с. (Допущено Министерством образования и науки в качестве учебника для студентов вузов).
-
Мирошник И.В. Теория автоматического управления. Линейные системы: Учебное пособие для вузов. СПб.: Питер, 2005. 336 с. (Рекомендовано УМО по университетскому политехническому образованию в качестве учебного пособия).
-
Никулин Е.А. Основы теории автоматического управления. Частотные методы анализа и синтеза систем: Учебное пособие для вузов. СПб.: БХВ-Петербург, 2004. 640 с. (Допущено УМО по университетскому политехническому образованию в качестве учебного пособия).
-
Востриков А.С., Французова Г.А. Теория автоматического регулирования: Учебное пособие для вузов. М.: Высшая школа, 2004. 365 с. (Рекомендовано УМО по образованию в области радиотехники, электроники, биомедицинской техники и автоматизации в качестве учебного пособия).
-
Ерофеев А.А. Теория автоматического управления: Учебник для вузов. 2-е изд., перераб. и доп. СПб.: Политехника, 2002. 302 с. (Рекомендовано Госкомитетом РФ по высшему образованию в качестве учебника).
-
Теория автоматического управления: Учебник для вузов /С.Е.Душин, Н.С.Зотов, Д.Х.Имаев и др.; Под ред. В.Б.Яковлева. М.: Высшая школа, 2003. 567 с. (Допущено Министерством образования РФ в качестве учебника).
