1.4. Постулат среднего арифметического /Гаусса/

Если одним и тем же измерительным прибором с одинаковой тщательностью произведем несколько измерений одной и той же физической величины и получим ряд случайных чисел, среди которых необходимо определить наиболее вероятное значение измеряемой величины, т.е. её значение, при котором плотность распределения достигает своего максимума. Эта задача решается с помощью постулата среднего арифметического. При выводе этого постулата воспользуемся методом наименьших квадратов, который заключается в следующем:

Если результаты измерений содержат случайные ошибки, распределенные по Гауссовскому закону, то наиболее вероятным значением измеряемой величины, является такое значение А, для которого сумма квадратов разностей этого значения и результатов измерений является наименьшей !

Найдем производную функции и приравняем её нулю. Откуда

• Следовательно, постулат среднего арифметического может быть сформулирован так: наиболее вероятнейшим значением измеряемой величины является среднее арифметическое из результатов наблюдений.

1.5. Определение среднеквадратической ошибки при косвенных методах измерений

При косвенных методах измерений искомую величину вычисляют как функцию, аргументы которой можно измерить непосредственно с некоторыми ошибками. В общем виде эта функция имеет вид

U = f ( x, y …).

Определим дифференциал данной функции и переходя от бесконечно малых приращений к конечным и, рассматривая их как погрешности измерения, мы получим

Для перехода к среднеквадратической погрешности воспользуемся выражением

,

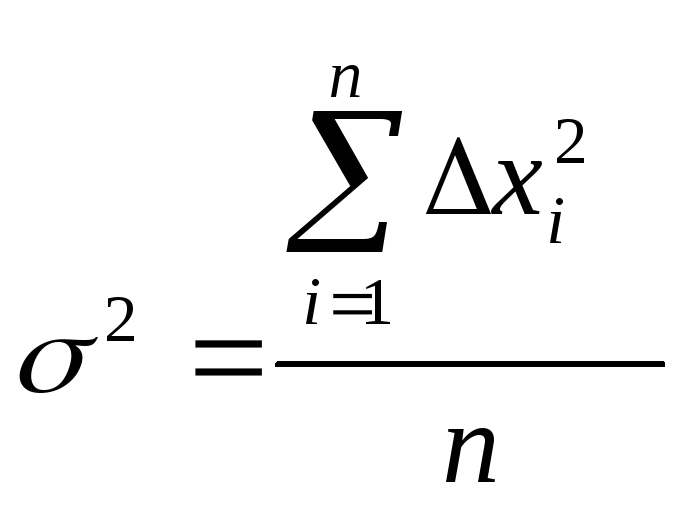причем считаем, что измерения каждого аргумента производятся n раз. После преобразования получаем

(4)

Рассматривая произведение как величину корреляции двух аргументов х иy, получим общую формулу

Нередко при анализе измерительного устройства в целом возникает задача суммирования погрешностей отдельных узлов и преобразователей. При этом можно использовать вышеприведенную формулу с учетом взаимокорреляционной связи между погрешностями, получаемыми в отдельных преобразователях и узлах прибора. Если ряд погрешностей одного или нескольких преобразователей вызывается одной и той же причиной, в результате чего они оказываются достаточно сильно коррелированными, то коэффициент взаимной корреляции принимается равным ±1 и формула суммирования погрешностей будет иметь вид

s²_å = s²₁ ± 2s₁s₂ +s²₂;

s_å = s₁ ± s₂.

Если же погрешности вызываются причинами, не имеющими между собой явной связи, то их коэффициент корреляции принимается равным нулю, формула для суммирования погрешностей будет иметь вид

s²_å = s²₁ + s²₂.

Примером жестко связанных между собой погрешностей являются погрешности отдельных измерительных преобразователей от случайных колебаний напряжения источника питания.

• Следовательно, при суммировании погрешностей, прежде всего, необходимо определить группы погрешностей с сильной корреляцией между собой. Внутри каждой из этих групп погрешности суммируются алгебраически с учетом их знаков, а результирующие погрешности, как слабо коррелированные между собой, складываются геометрически.