Лекция 23

Полосно-пропускающие фильтры

1. Общие вопросы

Полосно-пропускающий фильтр представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы , расположенной приблизительно вокруг центральной частоты ₀, рад/с, или , Гц. На рис. 1 изображены идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты _н и _в представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания _н <  < _в и ее ширину = _в – _н.

В полосе пропускания амплитудно-частотная характеристика никогда не превышает некоторого определенного значения, например А₁ (рис. 1). Существуют также две полосы задерживания 0 <  < ₁ и  > ₂, где значение амплитудно-частотной характеристики никогда не превышает заранее выбранного значения, например А₂. Диапазоны частот между полосами задерживания и пропускания, а именно ₁ <  < w_н и w_в <  < ₂, образуют соответственно нижнюю и верхнюю переходные области, в которых характеристика является монотонной.

Рис. 1. Идеальная и реальная амплитудно-частотные характеристики полосно-пропускающего фильтра

Добротность Q = ₀ / характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q – относительно широкая ширина полосы пропускания. Коэффициент усиления фильтра K определяется как значение его амплитудно-частотной характеристики на центральной частоте. Таким образом, K = Н(j₀).

Передаточные функции полосно-пропускающих фильтров можно получить из нормированных функций нижних частот переменной P с помощью преобразования

. (1)

Таким образом, порядок полосно-пропускающего фильтра в 2 раза выше, чем порядок соответствующего ему фильтра нижних частот и, следовательно, всегда является четным. Результирующая амплитудно-частотная характеристика полосно-пропускающего фильтра обладает центральной частотой ₀ и полосой пропускания и имеет сходство с характеристикой нижних частот, сдвинутой вверх по частоте от 0 до ₀. Таким образом, амплитудно-частотная характеристика полосно-пропускающего фильтра Баттерворта (полученная из функции Баттерворта нижних частот) изменяется монотонно в любую сторону от своего максимального значения и имеет максимально плоскую полосу пропускания (рис. 1). Крутизна изменения АЧХ (спада и подъема АЧХ) в два раза меньше, чем у ФНЧ и ФВЧ аналогичного порядка. Так, у ПФ второго порядка крутизна спада и подъема АЧХ – ±20 дБ/дек. Полосно-пропускающий фильтр Чебышева обладает пульсациями в полосе пропускания. В каждом случае центральная частота и частоты среза связанны следующим соотношением

₀ =,

где

(2)

На рис. 2 и 3 изображены примеры амплитудно-частотных характеристик фильтра Баттерворта четвертого порядка и фильтра Чебышева четвертого порядка с неравномерностью передачи 1 дБ для частоты ₀ = 1 рад/с при различных значениях добротности Q.

Рис. 2. Амплитудно-частотные характеристики полосно-пропускающего фильтра Баттерворта четвертого порядка

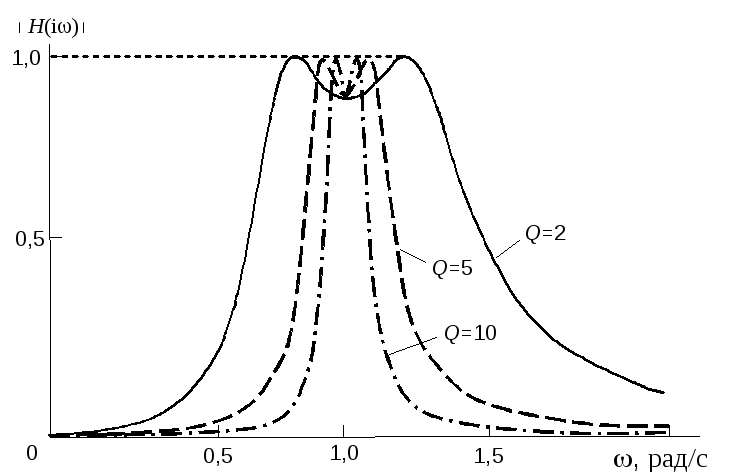
Рис. 3. Амплитудно-частотные характеристики полосно-пропускающего фильтра Чебышева четвертого порядка

Из этих результатов следует, что увеличение добротности Q приводит к более узким полосам пропускания.