Лекция 16

Интегрирующий усилитель

1. Принципы построения интегрирующего усилителя на оу

Операция интегрирования широко применяется при обработке и генерировании электрических сигналов. Напряжение на выходе интегратора прямо пропорционально интегралу от входного напряжения. В простейшем интеграторе, выполненном на основе инвертирующего усилителя (рис. 1, а), вместо резистора, соединяющего вход и выход ОУ, включается конденсатор.

аб

Рис. 1. Интегрирующий усилитель: а – схема интегрирующего усилителя; б – его частотная характеристика

Если ОУ идеальный (), то весь входной ток интегратора течет через конденсатор. Поскольку, то. Учитывая, что, получаем следующее выражение для выходного напряжения:

(1)

где приt = 0 – исходное входное напряжение интегратора.

На рис. 1 приведены амплитудно-частотные характеристики интегратора и ОУ без обратной связи с одним полюсом.

Передаточная функция инвертирующего усилителя находится по формуле . Асимптотическая ЛАЧХ такого идеального инвертирующего интегратора, соответствующая этой формуле, представлена на рис. 1.1,бштрихованной прямой (крутизна спадана всех частотах). Она имеет единственный полюс на частоте .

У реального интегрирующего усилителя на любой частоте коэффициент передачи , что делает частоту полюса. Из условиянайдем ее:.

Соответствующая асимптотическая ЛАЧХ линейно-ломаная. Кроме главного полюса она имеет, по меньшей мере, еще один полюс в области высших частот, что обусловлено спадом усиления ОУ.

Эквивалентная постоянная времени реального интегрирующего усилителя , определяющая частоту главного полюса, враз больше, чем. Следовательно, наличие ОУ эквивалентно увеличению емкости враз, что во столько же раз уменьшает требуемую емкость конденсатора, а значит, и его размеры.

Увеличение емкости здесь обусловлено эффектом Миллера. По существу он (эффект) состоит из ОУ и -интегратора, образованного резистором и емкостью Миллера. Следовательно, ОУ здесь выполняет две функции: создаети усиливает враз выходное напряжение пассивного интегратора, равное.

Напряжение весьма мало. Оно составляет малую часть входного напряжения схемы, что и обеспечивает малую погрешность интегрирования. В результате токчерез почти точно пропорционален входному напряжению.

Для построения прецизионных интеграторов, допускающих получение на выходе произвольных значений исходного выходного напряжения, можно воспользоваться схемой интегратора, показанной на рис. 2. Интегратор может работать в трех режимах: усиления, интегрирования и хранения – в зависимости от состояний переключателей , . Когдаразомкнут, а замкнут, интегратор преобразуется в инвертирующий усилитель, выходное напряжение которого (при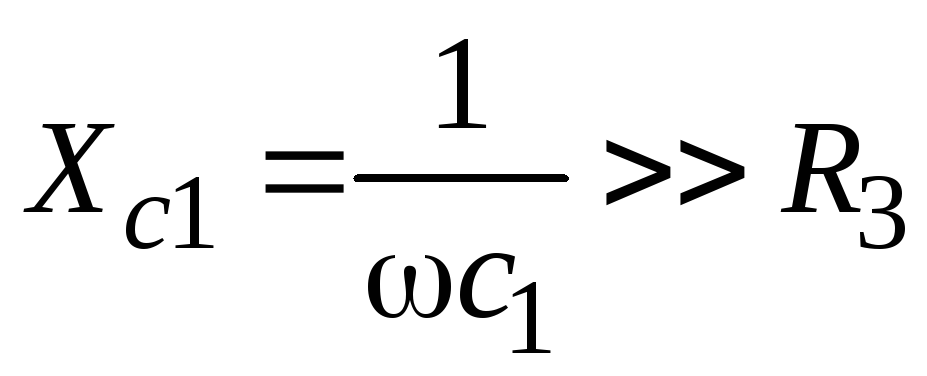). Когдазамкнут, а разомкнут, тогда осуществляется интегрирование входного напряжения:. И, наконец, когда размыкаются оба переключателяи , осуществляется хранение на конденсаторерезультата интегрирования.

Рис. 2. Схема универсального интегратора

2. Реакция интегрирующего усилителя на воздействие типовых сигналов

1. Ступенчатый сигнал

Входной ступенчатый сигнал как функция времени равен при , при (рис.3, а, б). Используя первое из этих условий, имеем:

.

аб

Рис. 3. Реакция интегратора на ступенчатый сигнал: а – входной сигнал,б– выходной сигнал

Таким образом, изменение выходного напряжения во времени представляет собой наклонную прямую с полярностью, противоположной полярности входного сигнала.

2. Прямоугольное колебание

Входное напряжение внутри периода повторения является функцией времени (рис. 4,а). Имеем = 5 В при , = –5 В при .

После интегрирования имеем , т.е. наклонную прямую на каждом полупериоде.

а б

Рис. 4. Реакция интегратора на прямоугольные колебания: а– входной сигнал,б– выходной сигнал

Накопленное напряжение в конце первого полупериода, т.е. интервала между при = 10кОм и = 0,1мкФ, :

.

Накопленное напряжение за второй полупериод между :

В.

Полученный выходной сигнал показан на рис. 1.4,б.Размах этого сигнала от пика к пику равен 2,5 В. При любом сигнале на входе изменение сигнала на выходе должно начинаться от того значения, которое выходной сиг­нал имел к моменту прихода входного сигнала.

3. Треугольный сигнал

На входе интегратора – пилообразное напряжение , показанное на рис. 4,б, как функция времени на интервале от , равное

, где .

Напряжение на выходе интегратора:

.

Таким образом, напряжение на выходе – это квадратичная функция вре­мени (парабола), показанная на рис. 5.

Рис. 5.Реакция интегратора на треугольный сигнал