Лекция 6

Оконечные и промежуточные усилительные каскады на биполярном транзисторе

В качестве оконечных и промежуточных каскадов могут использоваться каскады в схеме с ОЭ. Различие между промежуточными и оконечными каскадами заключается в том, что нагрузкой промежуточного каскада выступает входное сопротивление и ёмкость следующего каскада. Для оконечного каскада нагрузкой может выступать любое другое устройство. Нагрузка оконечного каскада носит, как правило, ёмкостный характер реактивной составляющей сопротивления.

Проанализируем каскад с ОЭ при емкостно-резистивной нагрузке. Принципиальная схема каскада приведена ниже.

Рис. 1

Для анализа этого каскада составим эквивалентную схему каскада. За основу возьмём упрощенную эквивалентную малосигнальную схему Джиаколетто.

Рис. 2

Здесь r_Б – распределённое сопротивление базы транзистора. r_Э – дифференциальное сопротивление эмиттерного перехода транзистора, которое можно рассчитать как r_Э = 0.026/I_К.

Тогда полная эквивалентная схема каскада:

Рис. 3

Обобщённый анализ такой схемы достаточно сложен. Но, зная, что усилитель достаточно широкополосный, т.е. отношение f_В/f_Н велико, можно упростить данную схему для различных частотных диапазонов АЧХ этого каскада.

1. Анализ каскада в области средних частот

В области средних частот можно считать, что большие разделительные ёмкости имеют реактивное сопротивление близкое к нулю, и пренебречь их влиянием. Также можно считать, что параллельные ёмкости малой величины (входная и выходная ёмкости транзистора, а так же ёмкость нагрузки) имеют очень высокое реактивное сопротивление, и их влиянием также можно пренебречь. Исходя из этого, эквивалентная схема каскада в области средних частот будет следующей.

Рис. 4

Очевидно, что в области средних частот, АЧХ усилительного каскада такого типа будет равномерной горизонтальной прямой, так как частотно-зависимые цепи в эквивалентной схеме отсутствуют.

1. Коэффициент усиления

Одним из основных параметров усилительного каскада является коэффициент усиления по напряжению. Для исследования этого параметра обратимся к входной характеристике транзистора.

Рис. 5

В некоторой точке, соответствующей току покоя базы транзистора, на этой характеристике можно провести касательную к кривой. Угол наклона  этой прямой будет характеризовать входную проводимость транзистора, tg() = R_{ВХ_ТР}. А так как I_К = I_Б, то значение источника тока в выходной цепи транзистора можно записать как

I = -U_БЭ/tg() = U_БЭ/ R_{ВХ_ТР} = U_БЭS.

где S=/ R_{ВХ_ТР} – крутизна усилительного прибора (транзистора) в рабочей точке. Минус перед напряжением база-эмиттер говорит о том, что ток коллектора противофазен входному току и напряжению.

Следовательно, напряжение на коллекторе можно записать как U_К=IR₀. R₀ в этом случае:

Поскольку коэффициент усиления К₀=U_ВЫХ/U_ВХ= U_К/U_БЭ, то учитывая что

получим

Следовательно, коэффициент усилительного каскада можно вычислить как:

Знак «минус» означает, что каскад инвертирует выходной сигнал, относительного входного.

2. Входное сопротивление

Для расчёта устройств подключаемых ко входу усилительного каскада зачастую необходимо знать входное сопротивление каскада. Рассмотрим входную цепь каскада. R_Г в состав каскада не входит. Влиянием R_Б можно пренебречь, так как её величина не несколько порядков больше входного сопротивления каскада, что будет показано далее. Таким образом, входная цепь каскада с ОЭ имеет следующий вид.

Рис. 6

Следует отметить, что через сопротивление r_Б протекает только базовый ток, а через сопротивление r_Э – и базовый и эмиттерный токи.

I_Э=I_К+I_Б=I_Б+I_Б=I_Б(+1)

Далее:

отсюда

3. Выходное сопротивление

Рассмотрим выходную цепь усилительного каскада в области средних частот.

Рис. 7

Очевидно, что в этом случае выходное сопротивление источника тока равно суммарному сопротивлению подключенных не нему параллельно сопротивлений, за исключением R_Н, не входящим в состав каскада. А поскольку R_i много больше чем R_К, то им можно пренебречь. Следовательно, R_ВЫХ = R_К.

4. Анализ каскада в области нижних частот

Построим эквивалентную схему каскада в области нижних частот. Учтём, что влиянием параллельных ёмкостей, вследствие их малости можно пренебречь.

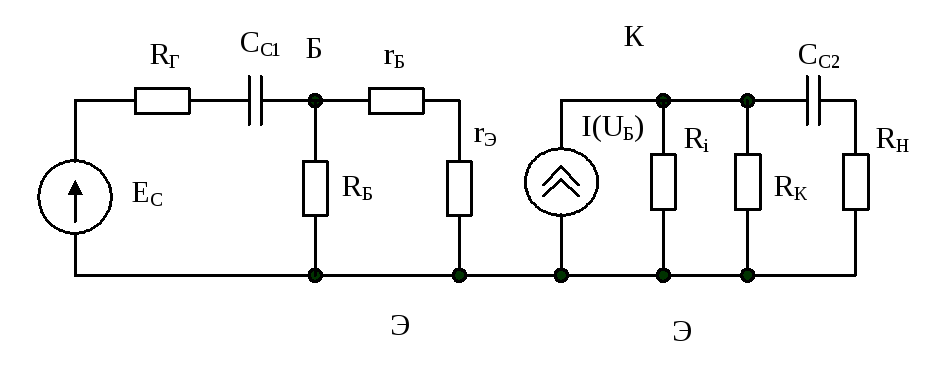
Рис. 8

Упростим эту схему, пользуясь знанием величины входного сопротивления и пренебрегая высоким сопротивлением R_i.

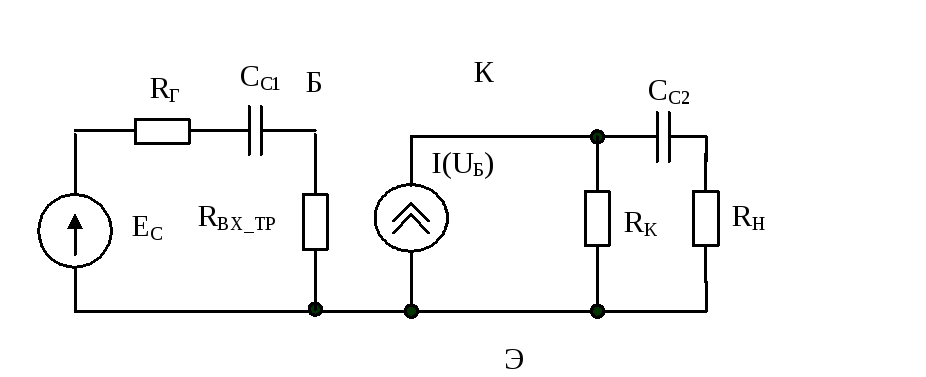
Рис. 9

Следует обратить внимание на то, что входная и выходная цепи этой эквивалентной схемы имеют одинаковую топологию (если учесть нулевое сопротивление источника напряжения). А именно П-образной RC цепи.

Исходя из этого, можно вычислить постоянные времени входной и выходной цепи в области нижних частот:

.

Отсюда нижняя граничная частота сквозного усиления:

,

где

.

5. Анализ каскада в области верхних частот

Построим эквивалентную схему каскада в области верхних частот. Учтём, что влиянием разделительных ёмкостей, вследствие малости их реактивного сопротивления на ВЧ можно пренебречь.

Рис. 10

Упростим эту схему, пользуясь знанием величины входного сопротивления и пренебрегая высоким сопротивлением R_Б и R_i.

Рис. 11

Следует обратить внимание на то, что входная и выходная цепи этой эквивалентной схемы имеют одинаковую топологию (если учесть нулевое сопротивление источника напряжения). А именно простой RC цепи.

Исходя из этого, можно вычислить постоянные времени входной и выходной цепи в области верхних частот:

,

.

Здесь в выражении для постоянной времени выходной цепи присутствует слагаемое − собственная постоянная времени транзистора, описывающая инерционные свойства самого транзистора.

Отсюда верхняя граничная частота сквозного усиления: