3. Передаточная характеристика фильтров Чебышева

Фильтр Чебышева нижних частот представляет собой оптимальный полиномиальный фильтр. Он обладает амплитудно-частотной характеристикой, которая определяется так:

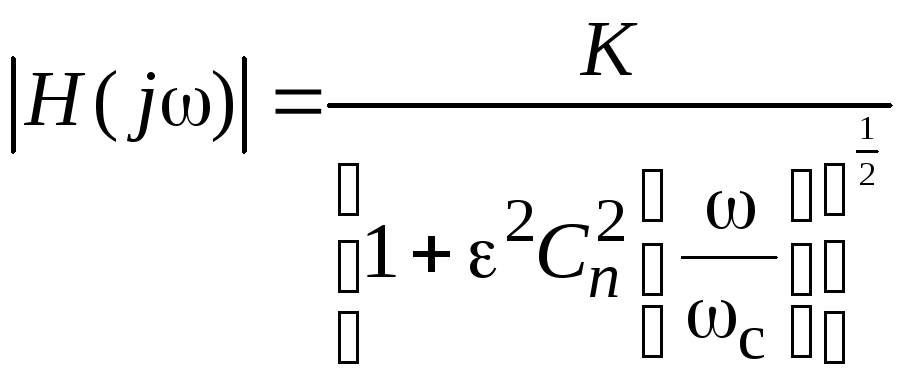
. (6)

Параметры иK– постоянные числа;С_n – является полиномом Чебышева первого рода степениnи имеет вид

.

Амплитудно-частотная характеристика достигает своего наибольшего значения Kв тех точках, гдеС_n равно нулю. Поскольку эти точки распределены по полосе пропускания, то характеристика фильтра Чебышева содержит пульсации в полосе пропускания и является монотонной в других областях.

Размах этих пульсаций определяет параметр , а их число – степеньп. Коэффициент усиления филь­тра определяется значениемK.

На рис. 6 изображена АЧХ фильтра Чебышева при K= 1 и= 1 рад/с.

Рис. 6. Амплитудно-частотные характеристики фильтра Чебышева нижних частот

Минимально допустимое затухание в полосе пропускания – постоянный размах пульсации, часто выражается в децибелах как

. (7)

Наибольшим допустимым размахом пульсаций обладает фильтр Чебышева с неравномерностью передачи 3 дБ, для которого в (7) = 1.

Передаточные функции фильтров Чебышева нижних частот по форме идентичны функциям фильтра Баттерворта, определенным ранее.

Амплитудно-частотная характеристика фильтра Чебышева данного порядка лучше амплитудно-частотной характеристики Баттерворта, так как у фильтров Чебышева ширина переходной области меньше. Однако фазочастотная характеристика фильтра Чебышева хуже (более нелинейная) по сравнению с фазочастотной характеристикой фильтра Баттерворта. Можно также отметить, что фазочастотные характеристики фильтров Чебышева высокого порядка хуже фазочастотных характеристик фильтров более низкого порядка. Это высказывание согласуется с тем фактом, что амплитудно-частотная характеристика фильтра Чебышева высокого порядка лучше амплитудно-частотной характеристики фильтра более низкого порядка.

4. Фильтры нижних частот с многопетлевой обратной связью и бесконечным коэффициентом усиления (инвертирующее включение оу)

Для фильтра нижних частот второго порядка с частотой среза _с типовая полиномиальная передаточная функция имеет следующий вид:

. (8)

Постоянные ВиСпредставляют собой нормированные коэффициенты, поскольку для_с= 1 эта передаточная функция приводится к виду (2) приn= 2. Для фильтров Баттерворта и Чебышева эти коэффициенты приведены в прил. 1. ПостояннаяKопределяет коэффициент усиления, который, конечно, также необходимо точно задать.

Для фильтров более высокого порядка уравнение (8) описывает передаточную функцию типового звена второго порядка, где K– коэффициент его усиления;ВиС– коэффициенты звена, приведенные в прил. 1.

Одна из наиболее простых схем активных фильтров, реализующих передаточную функцию нижних частот согласно (8), приведена на рис. 1.10. Она иногда называется схемной с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления из-за наличия двух путей прохождения сигнала обратной связи через элементы С₁иR₂, а также вследствие того, что ОУ в этом случае работает как прибор с бесконечным коэффициентом усиления. Эта схема реализует уравнение (8) с инвертирующим коэффициентом усиления –K(K> 0) и

(9)

Сопротивления, удовлетворяющие уравнению (9):

(10)

Сопротивления задаются в омах, а емкости – в фарадах.

Следовательно, по заданным K, В, Си_сможно выбрать значениеС₁иС₂и вычислить требуемые значения сопротивлений. Емкости должны иметь номинальные значения, которые в результате расчета дают реальное значение сопротивленияR₂. Это условие выполняется, если

. (11)

Рис. 7. Схема фильтра нижних частот с МОС второго порядка

Целесообразный подход состоит в том, чтобы задать номинальное значение емкости С₂, близкое к значению 10/f_cмкФ и выбрать наибольшее имеющееся номинальное значение емкостиС₁, удовлетворяющее уравнению (11). Сопротивления должны быть близки к значениям, вычисленным по (10). Чем выше порядок фильтра, тем более критичными являются эти требования.

Пример.Предположим, что необходимо разработать фильтр Чебышева с МОС второго порядка с неравномерностью передачи в полосе пропускания= 0,5 дБ, полосой пропускания 1000 Гц и коэффициентом усиления, равным 2. В этом случаеK= 2,_с= 2· 1000, а из прил. 1 находим, чтоВ= 1,425625 и С= 1,516203. Выбирая номинальное значениеС₂= 10/f_c= =10/1000 = 0,01 мкФ, из (11) получаеммкФ.

Выберем номинальное значение емкости С₁= 0,001 мкФ = 1 нФ и вычислим по (10) значения сопротивлений. В результатеи.

Пример.Предположим, что необходимо разработать фильтр Баттерворта шестого порядка с МОС, частотой среза f_c = 1000 Гц и коэффициентом усиления K = 8. Он будет состоять из трех звеньев второго порядка, каждое с передаточной функцией, определяемой уравнением (1). Выберем коэффициент усиления каждого звена K = 2, что обеспечивает требуемый коэффициент усиления самого фильтра . Из прил. 1 для первого звена находимВ = 0,517638 и С = 1. Снова выберем номинальное значение емкости С₂ = 0,01 мкФ и в этом случае из (11) найдем С₁ < 0,00022 мкФ. Зададим номинальное значение емкости С₁ = 200 пФ и из (10) найдем значение сопротивлений R₂ = 139,4 кОм; R₁ = 69,7 кОм; R₃ = 90,9 кОм.

Два других звена рассчитываются аналогичным способом, а затем звенья соединяются каскадно для реализации фильтра Баттерворта шестого порядка. Результирующая схема имеет амплитудно-частотную характеристику, показанную ранее на рис. 5.

Из-за своей относительной простоты фильтр с МОС является одним из наиболее популярных типов фильтров с инвертирующим коэффициентом усиления. Он обладает также определенными преимуществами, а именно хорошей стабильностью характеристик и низким выходным полным сопротивлением; таким образом, его можно сразу соединять каскадно с другими звеньями для реализации фильтра более высокого порядка. Недостаток схемы состоит в том, что невозможно достичь высокого значения добротности Qбез значительного разброса значений элементов и высокой чувствительности к их изменению. Для достижения хороших результатов коэффициент усиленияKи добротностьQдолжны быть ограничены значением, приблизительно равным 10. Коэффициент усиления может быть больше, если значение добротности выбрано меньшим и выполняется ограничение, например:KQ= 100 приQ<10.