Лекция 6. Основная волна типа н10 прямоугольного волновода

Обычно волновод проектируют таким образом, чтобы в нём распространялась одна основная волна (одномодовый режим). Определим частотный диапазон, в котором возможно распространение только основной волны и невозможно распространение других. Частотный рабочий диапазон, при котором распространяется только Н₁₀

< < , < < (2.21)

Заполнение волновода диэлектриком смещает частотный диапазон в низкочастотную область. Для заданного частотного диапазона необходимо выбрать поперечные размеры волновода, исходя из условия распространения волн

> > ; < ; < b< Итак, < < , b< и более жёсткое условие b< . (2.22)

Поперечные размеры прямоугольных волноводов соизмеримы с длиной волны, поэтому в основном они используются в сантиметровом диапазоне, частично в дециметровом и миллиметровом диапазонах. Обычно принимают

, . (2.23)

В качестве средней длины волны рабочего диапазона рекомендуется величина

. (2.24)

Если b < 0,5 а, то область, где распространяется только основной тип волны Н₁₀, определяется соотношением . На практике рекомендуются следующие использования допустимой полосы длин волн:

, . (2.25) .

Приведем выражения, описывающие пространственную зависимость комплексных амплитуд декартовых проекций векторов электромагнитного поля для волны типа Н₁₀ , подставляя индексы m=1 и n=0 в общие формулы (2.14):

(2.26)

Иногда удобно выразить амплитуды через максимальную амплитуду электрического поля Е₀, которая максимальна в середине широкой стенки. Укажем распределение амплитуд составляющих векторов поля по координатам: вдоль оси z амплитуды постоянны (как и у любой бегущей волны), амплитуды постоянны и по координате y (так как индекс n=0), по координате x – амплитуды имеют тригонометрическую зависимость. Цифра 1 в записи H₁₀ означает, что все составляющие электромагнитного поля имеют одну вариацию поля вдоль оси oх. Цифра 0 означает, что все компоненты поля имеют постоянное распределение вдоль оси oy (0 вариаций).

На рис. 2.2 показано распределение по модулю амплитуд составляющих векторов поля, нормированных к максимальному значению

Рис. 2.2 Распределение амплитуд составляющих векторов поля.

Параметры волны Н₁₀ рассчитываются по общим формулам направляемых волн. Длина волны

(2.27)

Следует отметить, что при изменении длины волны генератора λ₀ длина волны в волноводе λ_в изменяется непропорционально ей. Закон зависимости длины волны в волноводе от длины волны в свободном пространстве называется дисперсионной характеристикой волновода (график на рис.2.3).

Область λ₀ < λ_кр является областью прозрачности. При λ₀ << λ_кр λ_в  λ₀. Если λ₀  λ_кр, то λ_в  ∞. При переходе λ₀ за граничные значения λ₀ в волноводе существует не бегущая волна, а колебание, экспоненциально затухающее вдоль продольной оси oz.

Рис. 2.3 Дисперсионная характеристика прямоугольного волновода

С фазовой скоростью распространяется фронт волны внутри волновода

(2.28)

Передача же сигнала по волноводу происходит с групповой скоростью

(2.29)

Видно, что групповая скорость всегда меньше фазовой и скорости света.

Характеристическое сопротивление волновода. По физическому смыслу характеристическое сопротивление линии передачи – это отношение некоторой электрической характеристики волнового процесса к магнитной. В теории волноводов характеристическое сопротивление определяется как отношение модулей поперечных составляющих векторов напряженности электрического и магнитного полей. Для волны H₁₀ характеристическое сопротивление вычисляется по формуле

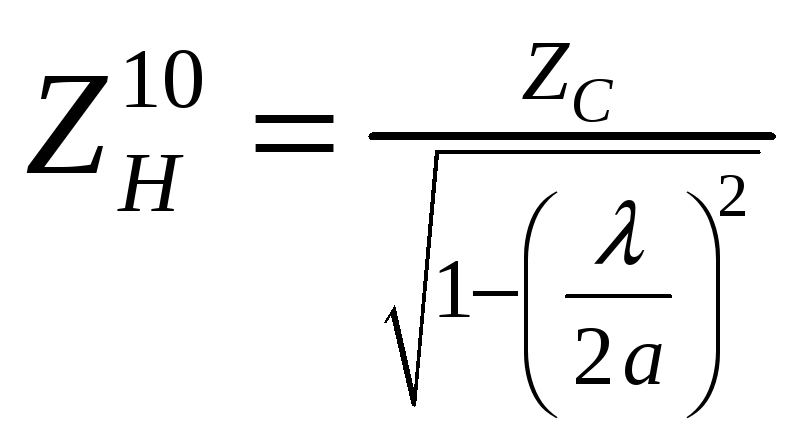(2.30)

Характеристическое сопротивление широко используется в различных прикладных задачах (например, в задачах согласования, т.е. отсутствия отраженной волны). Через сопротивления можно оценить излучение из открытого конца волновода. Волноводу сопоставляется эквивалентная схема в виде полубесконечной линии с сопротивлением и нагрузки с сопротивлением Z_С, равным сопротивлению свободного пространства. Используем коэффициент отражения на границе двух сред. Погрешность этой формулы в данном случае составляет 10%-15%, так как не учитываются высшие типы, возникающие на открытом конце волновода. Через коэффициент отражения считается . Обычно коэффициент отражения невелик на волне Н₁₀ и открытый конец волновода может служить эффективной антенной в СВЧ диапазоне.

Волновое сопротивление ρ волноводов не может быть определено однозначно, как это будет сделано с линиями с волной типа Т. В соответствии с законом Ома волновое сопротивление может быть определено тремя способами: через мощность и эквивалентное напряжение, через мощность и эквивалентный ток и через напряжение и ток.

В прямоугольном волноводе с волной H₁₀ соответствующие волновые сопротивления записываются следующим образом:

Поляризация поля волны Н₁₀. По электрическому полю поляризация всегда линейная, так как волна имеет одну составляющую Е_y. У магнитного поля две составляющие Н_Х и Н_Z, они сдвинуты по фазе на и в общем случае вектор Н будет иметь эллиптическую поляризацию в плоскости, параллельной широкой стенке волновода. Но вид поляризации зависит еще от соотношения амплитуд этих составляющих :, и в разных точках по координате х поляризация по вектору Н меняется:

и , - поляризация линейная;

, – вновь поляризация линейная.

Определим координату x , когда амплитуды Н_Х и Н_Z (2.26) равны:

, (2.31)

На расстоянии (2.31) от узкой стенки волновода вектор Н имеет круговую поляризацию в плоскости, параллельной широкой стенке волновода.

Структуру поля принято иллюстрировать расположением, густотой и формой силовых линий векторов Е и Н в трёх ортогональных сечениях волновода. При этом должны соблюдаться положения, вытекающие из уравнений Максвелла и граничных условий:

1. силовые линии вектора Н замкнуты и касательны идеально проводящей поверхности. Силовые линии вектора Е перпендикулярны идеально проводящей поверхности, они замкнуты и могут прерываться на поверхностных зарядах;

2. силовые линии векторов Е и Н взаимно ортогональны, их направления

таковы, что вектор Пойнтинга (плотность потока мощности) направлен вдоль линии;

3. картина поля рисуется в фиксированный момент времени, и со временем перемещается вдоль волновода с фазовой скоростью соответствующей волны.

Структура силовых линий векторов электромагнитного поля волны Н₁₀ приведена на рис. 2.4а в 3-х проекциях;

на рис. 2.4б, 2.4в в 2-х проекциях и в двух режимах;

на рис.2.5 в объеме волновода.

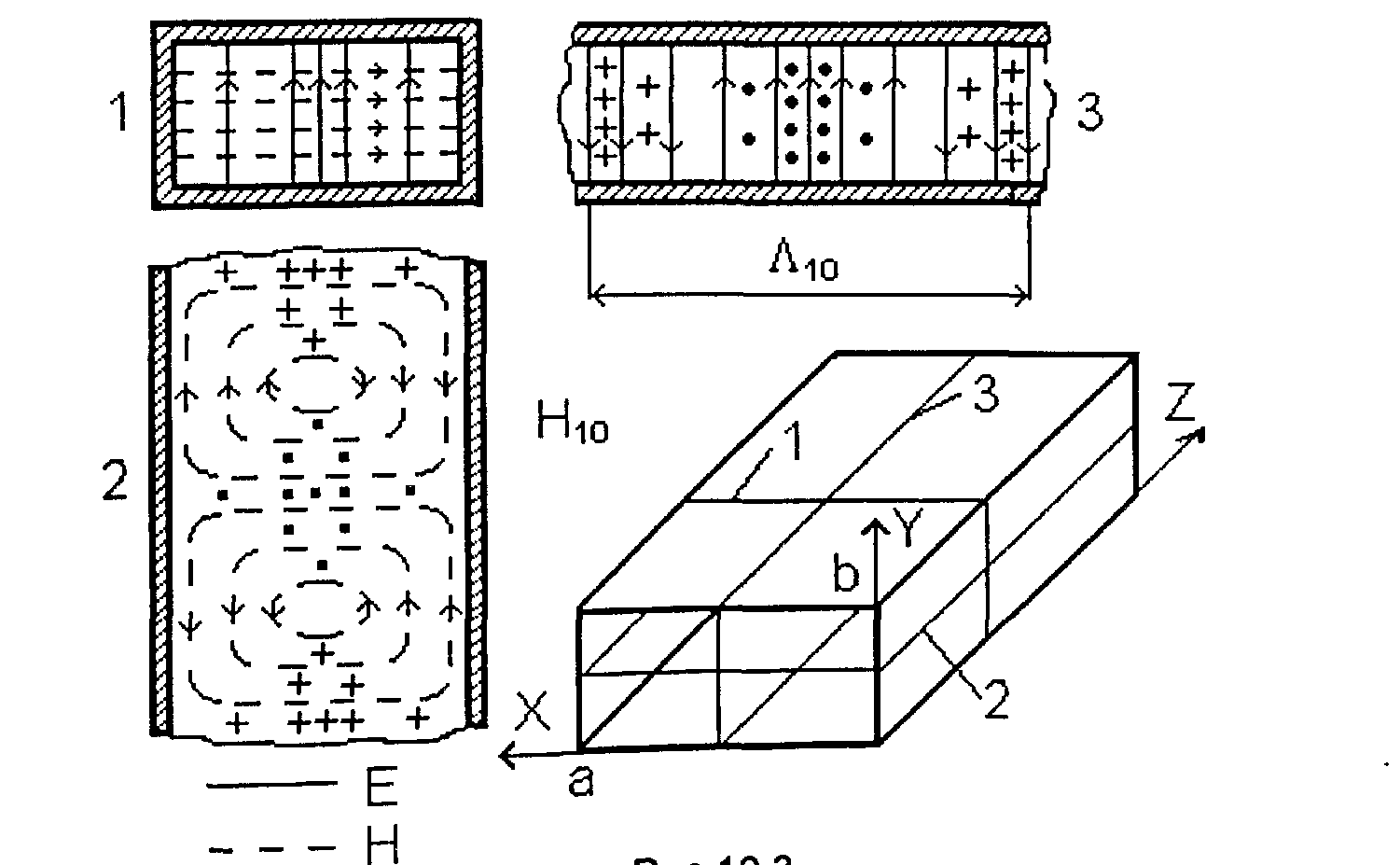
Рис. 2.4 а Структура поля бегущей волны Н₁₀

Рис. 2.4б. Прямоугольный волновод с волной H₁₀

Сплошные линии – силовые линии вектора Е, штриховые – вектора Н.

Режим бегущей волны

Рис. 2.4в. Прямоугольный волновод с волной H₁₀

Сплошные линии – силовые линии вектора Е, штриховые – вектора Н.

Режим стоячей волны

Рис.2.5 Структура поля волны Н₁₀

Распространение электромагнитной волны внутри волновода сопровождается наведением переменного тока проводимости, поверхностная плотность распределения которого по граничным условиям

, (2.32)

где - внутренняя нормаль к стенке (нормаль со стороны поля);

- напряженность магнитного поля у стенки.

Поскольку картина распределения силовых линий вектора напряженности магнитного поля в волне рассматриваемого типа известна, построение линий тока на стенка волновода не представляет затруднений: эти линии образуют семейство кривых, ортогональных семейству силовых линий напряженности магнитного поля. На рис. 2.6 показана картина силовых линий вектора на стенках короткозамкнутого волновода, работающего на волне Н₁₀. Линии поверхностного тока проводимости на стенках замыкаются линиями тока смещения, совпадающими по направлению с линиями вектора во внутреннем пространстве волновода.

КЗ стенка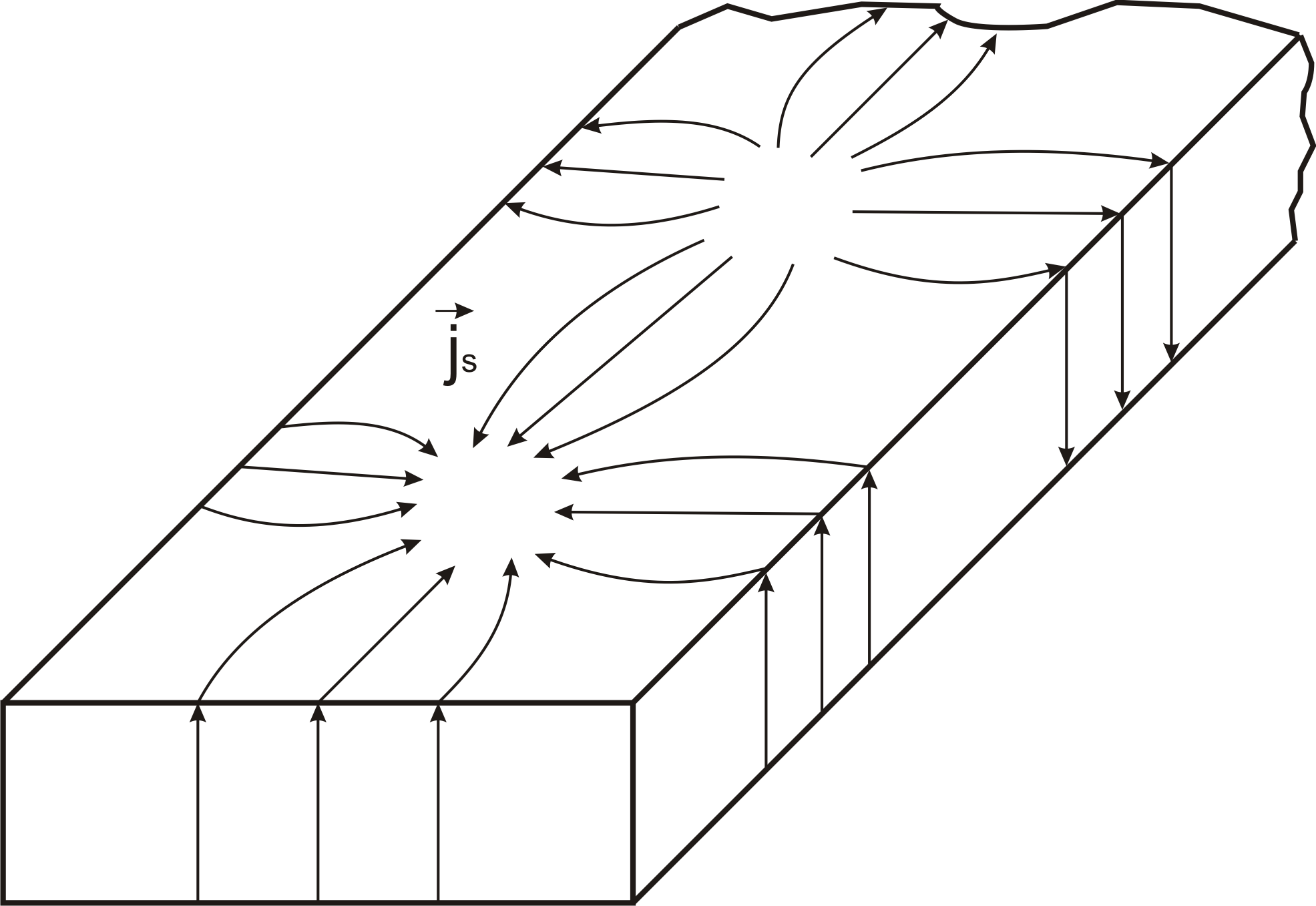

Рис. 2.6. Распределение токов на стенках короткозамкнутого волновода

Мощность, переносимая по прямоугольному волноводу волной H₁₀. Как видно из формул (2.26), поперечные составляющие векторов поля E_y и H_х находятся в фазе, откуда следует, что вектор Пойнтинга является величиной действительной и направлен вдоль оси oz. Усредненная за период колебания мощность, переносимая вдоль оси волновода, определяется как интеграл от вектора Пойнтинга по поперечному сечению волновода. Мощность бегущей волны Н₁₀ вычисляется по общей формуле

(2.33)

Выражение (2.33) дает возможность определить предельно допустимую мощность, передаваемую по прямоугольному волноводу. Наибольшая амплитуда E_макс не должна превосходить определенного уровня, выше которого наступает электрический пробой среды, заполняющей волновод. Для сухого атмосферного воздуха при нормальном давлении E_{макс.проб} = 30 кВ/см. При стандартных размерах волновода (λ_ср в сантиметрах). При λ = 30см , допустимое значение . Как видно в дециметровом диапазоне по прямоугольному волноводу стандартных размеров (, ) можно передать значительную мощность. Однако по мере повышения частоты допустимая мощность быстро уменьшается и при λ = 1см не превышает 30…45кВт.

Выделим в формуле (2.33) сомножитель

, (2.34)

характеризующий удельную мощность, переносимую через единичную площадку. Если положить, что на центральной частоте рабочего диапазона волновода с воздушным заполнением величина λ₀ /2а = 0,7, и подставить предельно допустимую напряженность электрического поля, то для волны H₁₀ получим

P_{уд. доп} = 420 кВт/см² . (2.35)

При проектировании волноводных трактов с высоким уровнем мощности вследствие возможных отражений вводят почти трехкратный запас, снижая указанный уровень до 150 кВт/см².

Затухание волны H₁₀ в волноводе обусловлено потерями энергии в металлических стенках волновода. Погонный коэффициент затухания рассчитывается по общей формуле (глава 1) и для волны H₁₀ выражается

, (2.36)

где – активное поверхностное сопротивление металла с проводимостью .

Волна Н₁₀ имеет наименьшие потери в прямоугольном волноводе по сравнению с другими (рис 2.7)

Рис. 2.7. График зависимости коэффициента ослабления α_м (в дБ/м) от частоты для волн H₁₀, H₂₀ и E₁₁ в случае медного волновода поперечного сечения: а=51 мм, b= 25мм.

На частотах, близких к , по концепции парциальных волн всё большее число отражений приходится на единицу длины. При каждом отражении часть энергии парциальной волны теряется из-за неидеальной проводимости металла и потери резко возрастают. При увеличении частоты коэффициент затухания уменьшается до тупого минимума и затем вновь начинает возрастать за счет уменьшения скин-слоя и увеличения поверхностного сопротивления стенок волновода. Минимум затухания поля волны Н₁₀ при соотношении сторон поперечного сечения 2:1 наблюдается при . Поведение вблизи определяет выбор рабочего диапазона:

теоретически ^;

на практике рекомендуется следующая полоса длин волн;

(2.37)

В коротковолновой части сантиметрового диапазона потери в стандартных волноводах достаточно велики. Например, λ = λ₀ = 1см в стандартном волноводе с медными стенками и при длине линии всего 10м потери энергии составляют 5,5 дБ (более 70% входящей мощности). Уменьшение поперечных размеров волновода сопровождается возрастанием плотности поверхностного тока проводимости в его стенках и соответственно возрастанием потерь.

Коэффициент затухания в диэлектрике рассчитывается по общей формуле для направляемых волн

(2.38)

По конструктивной реализации волноводы могут быть жесткими и гибкими. В последнем случае стенки делают гофрированными (рис.8.8).

Контрольные вопросы

1. Перечислите преимущества и недостатки волноводных линий передачи

2. Нарисуйте графики изменения длины волны в волноводной линии от частоты. Чем можно объяснить такое поведение графиков?.

3. Определите частотный диапазон работы прямоугольного го волновода на основном типе колебаний?

4. Что такое ортогональность типов волн в волноводах?

Задачи для самостоятельного решения

1. Какие типы волн могут распространяться в квадратном волноводе со стороной 1 см при частоте 10 ГГц? Волновод заполнен диэлектриком с относительной проницаемостью  = 2,6.

2. Определить критическую длину волны, критическую частоту и длину волны в прямоугольном волноводе для основного типа H₁₀. Размеры поперечного сечения волновода 23х10 мм. Частота колебаний 10 ГГц (внутренняя среда - воздух).

3. Определить критическую длину волны, критическую частоту и длину волны в прямоугольном волноводе для волны типа Е₁₁. Размеры поперечного сечения 4х3 см. Частота колебаний 10 ГГц.

4. Прямоугольный волновод сечением 23х10 мм заполнен диэлект­риком ( = 2,25,  = 0, μ = 1). Частота колебаний 8,4 ГГц. Определить фазовую скорость и длину волны основного типа колебаний.

5. Фазовая скорость волны типа H₁₀ в прямоугольном волноводе равна 5 с, где с – скорость света. Определить размеры волновода, если длина волны в свободном пространстве равна 10 см.