Глава 2. Прямоугольный металлический волновод

Лекция 4. Поле в прямоугольном волноводе

Прямоугольный волновод представляет собой полую металлическую трубу прямоугольного сечения (рис.2.1). Волновод используется как линия передачи в основном в сантиметровом диапазоне длин волн, частично в дециметровом и миллиметровом диапазонах. Примеры наиболее распространённых стандартных волноводов следующих поперечных размеров (широкую стенку принято обозначать через «а», узкую – «b»):

а х b = 1,6 х 0,8 мм (λ_ср ~ 2 мм)

23 х 10 мм (λ_ср ~ 3 см)

72 х 34 мм (λ_ср ~ 10 см)

110 х 55 мм (λ_ср ~ 15 см)

Задача определения поля в волноводе решается в предположении, что стенки волновода обладают бесконечной проводимостью, а заполняющая его среда - идеальный диэлектрик с параметрами  и .. Волновод бесконечно протяжённый (чисто бегущая волна). Поле монохроматическое. Будем считать, что источник находится за пределами рассматриваемой части линии передачи и создаваемая им волна распространяется вдоль оси z. Используемая система координат и размеры a и b поперечного сечения волновода показаны на рис.2.1.

Рис. 2.1. Прямоугольный волновод

В прямоугольном металлическом волноводе с однородным диэлектрическим заполнением распространяются магнитные волны типа , у которых компоненты H_Z  0, a E_Z = 0 (направление оси z совпадает с продольной осью волновода), и электрические волны , у которых E_Z  0, H_Z = 0. Поперечно электромагнитные Т-волны не существуют. Предположим, что Т волна существует, у которой Е_Z = 0, Н_Z = 0, Е_┴ ≠ 0, Н_┴ ≠ 0. Силовые линии вектора Н^→ замкнуты, в данном случае лежат в поперечной плоскости и согласно первому уравнению Максвелла охватывают линии вектора объёмной плотности полного тока:

Но у волны Т продольная составляющая Е_Z = 0, уравнение Максвелла не выполняется, и волна Т не существует. Здесь же можно сделать вывод, что если внутри линии есть проводник, то Т волна существует. Но это уже другой тип линии передачи (например - коаксиальная линия).

Так как поперечные составляющие векторов поля однозначно определяются через продольные (см. 1.15,1.16), то для определения поля электрических и магнитных волн достаточно решить однородные волновые уравнения Гельмгольца для продольных составляющих векторов поля

Уравнения одинаковые по структуре, достаточно заняться решением одного из них. Волна распространяется вдоль оси z.

Амплитуда Е _mz (х,у) зависит от поперечных координат, фаза βz описывает линейное изменение фазы поля вдоль координаты распространения z. При явной зависимости от z, можно сразу расписать вторую производную в операторе Лапласа:

Далее учтём, что _┴, сократим е^-jβz и уравнения Гельмгольца приводим к виду

(2.1) (2.2)

Эти уравнения решаем методом разделения переменных, согласно которому искомое решение представляется в виде произведения двух функций, каждая из которых зависит только от одной переменной. Займемся первым волновым уравнением (2.1).

(2.3)

Для определения неизвестных функций X(x) и Y(y) искомое решение (2.3) подставляем в (2.1) и делим на произведение X(x)Y(y)

(2.4)

(2.5)

В уравнении (2.5) сумма двух независимых функций (первое и второе слагаемые) равна постоянной величине. Это возможно только при условии, что сами функции равны пока неизвестным постоянным, называемыми константами разделения

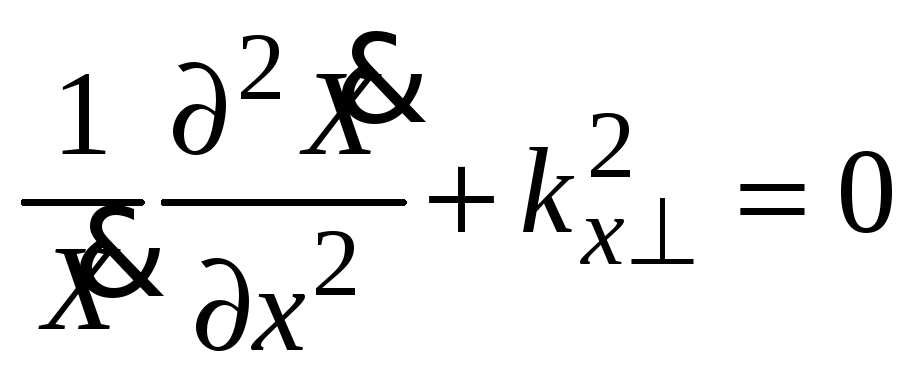
(2.6)

При этом должно выполняться равенство

(2.7)

Решая полученные уравнения (2.6), находим

(2.8)

(2.9)

Неизвестные постоянные , определяем из граничных условий: на идеально проводящих стенках волновода касательная составляющая вектора напряженности электрического поля равна нулю. В случае электрических волн (решаем уравнение 2.1) продольная составляющая E_mz является касательной ко всем стенкам волновода. Поэтому уравнения (2.3,2.8,2.9) должны быть подчинены следующим граничным условиям:

При х=0 коэффициент В=0; при х=a функция .

Коэффициент A≠0, иначе Е_Z = 0, что невозможно для Е волн. Значит, , аргумент синуса , и неизвестная константа разделения принимает вид:

, индекс m имеет числовые значения (2.10)

При y=0 коэффициент D=0; при у=b функция .

Коэффициент С≠0, иначе Е_Z = 0, что невозможно для Е волн. Значит, , аргумент синуса , и неизвестная константа разделения принимает вид:

, индекс n имеет числовые значения (2.11)

В случае электрических волн значения индексов m = 0 и n = 0 не годятся, так как при этом E_mz = 0 во всех точках внутри волновода. Найденное решение для продольной составляющей E_mz принимает вид

(2.12)

В формуле (2.12) введено обозначение E_0z = AC – максимальная амплитуда продольной составляющей вектора Е. Величина E_0z определяется либо заданием конкретного источника, либо заданием мощности бегущей волны. Для дальнейшего анализа конкретное значение не требуется. Волновод является линейной системой, и безразлично, на каком уровне поля проводить его анализ. Через найденную продольную составляющую (2.12) поперечные составляющие векторов поля определяются из соотношений (1.16).

Электромагнитное поле распространяющейся волны имеет компоненты:

,

,

,

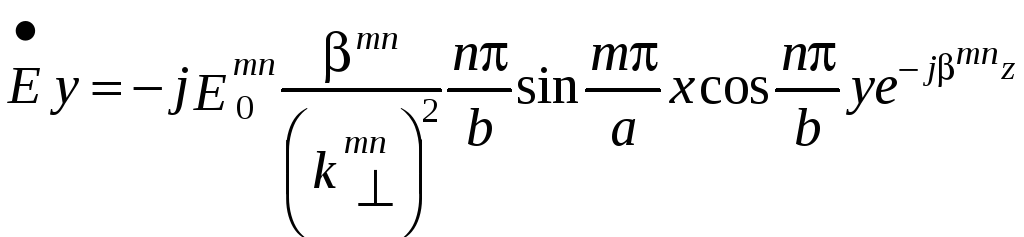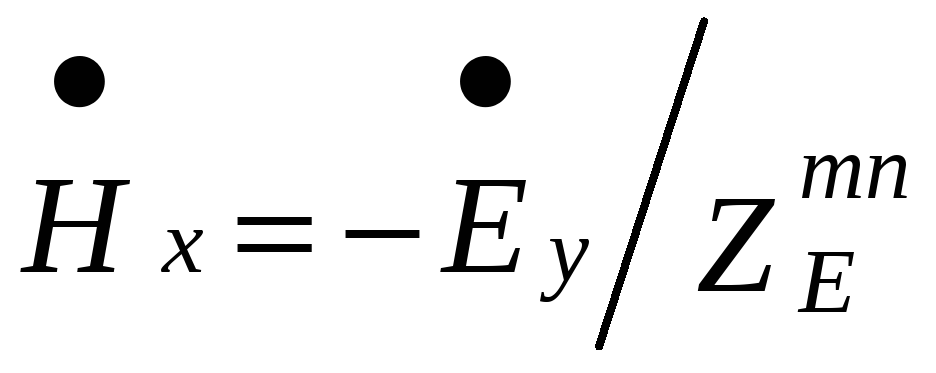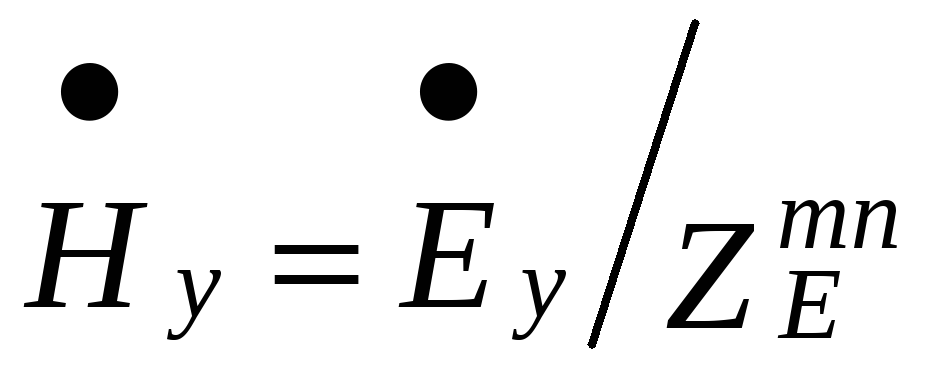, , , (2.13)

где – характеристическое сопротивление волновода с

волной ;

[Ом] – характеристическое сопротивление cреды, заполняющей волновод;

– продольное волновое число (коэффициент фазы);

– поперечное волновое число.

Электрические и магнитные волны имеют много общих черт, и их свойства удобно анализировать совместно. В случае магнитных волн решение уравнения для продольной составляющей (2.2) проводится так же, как и для электрических волн. Видоизменяется только запись граничных условий.

Электромагнитное поле распространяющейся волны имеет компоненты:

,

,

,

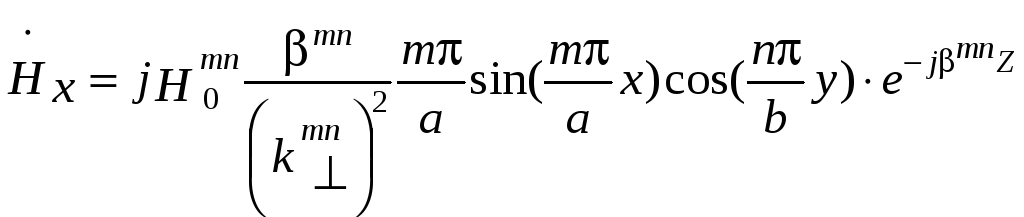, , , (2.14)

где 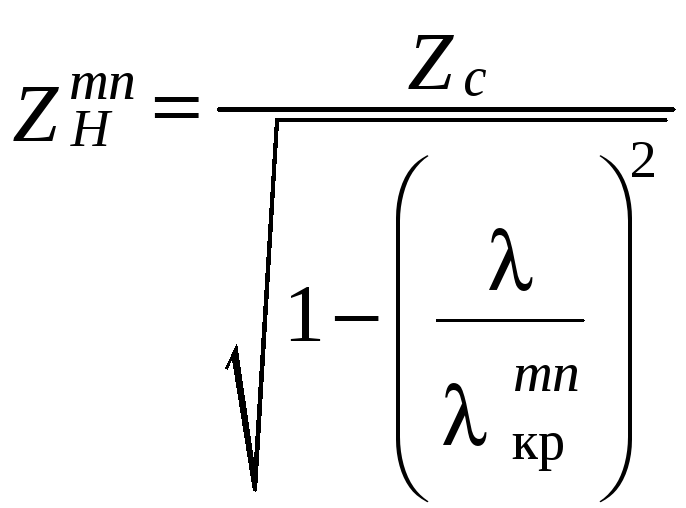[Ом] – характеристическое сопротивление волновода для волн типа .

В отличие от электрических волн для магнитных волн индексы m и n могут принимать нулевые значения, но они не могут равняться нулю одновременно, так как при этом продольная составляющая H_z не зависит от переменных x и y и вектор Е (см. 1.5) будет равен нулю.

Значение искомого поперечного волнового числа (2.7) получаем из приведенного решения, а вслед и значение критической длины волны для электрических и магнитных волн

(2.15)

Каждой паре индексов (чисел) m и n соответствует определённое поле, называемое типом волны, или гармоникой, или модой (от латинского слова modus – образ). Обозначаются они Е_mn или Н_mn и в волноводе может существовать бесконечный спектр электрических и магнитных волн. Не существуют в силу граничных условий (Е_τ=0 на идеально проводящей стенке) волны Н₀₀, Е₀₀, Е_m0, Е_0n. Индекс m в записи волны означает, что все составляющие электромагнитного поля имеют m вариаций поля вдоль оси oх, а индекс n означает число вариаций поля вдоль оси oy.

Для нескольких первых типов волн значения критической длины волны приведены в таблице

	m=0	m=1	m=2
n=0	-	2a	a
n=1	2b
n=2	b