Глава 4. Линии передачи с волнами типа т

Лекция 8. Коаксиальная линия передачи

Линии передачи с волнами типа Т не имеют критической частоты, то есть начинают работать с нулевой частоты. Положительным качеством линий передачи с волнами рассматриваемого типа является слабая зависимость их параметров от частоты. Эти линии обладают слабой дисперсией.

Волны типа Т не имеют продольных по отношению к направлению распространения компонентов поля. Имеются лишь поперечные составляющие векторов поля. Волны такого вида называются поперечными электромагнитными или волнами типа Т.

Наиболее широко используемой линией с волной типа Т является коаксиальный волновод, который представляет собой два соосных металлических цилиндра с диаметрами центрального проводника (=2а=2R₁) и экрана (=2b=2R₂), разделенных диэлектриком с относительной диэлектрической проницаемостью . Используемая цилиндрическая система координат и диаметры (радиусы) поперечного сечения линии показаны на рис.4.1.

Рис. 4.1. Коаксиальный волновод

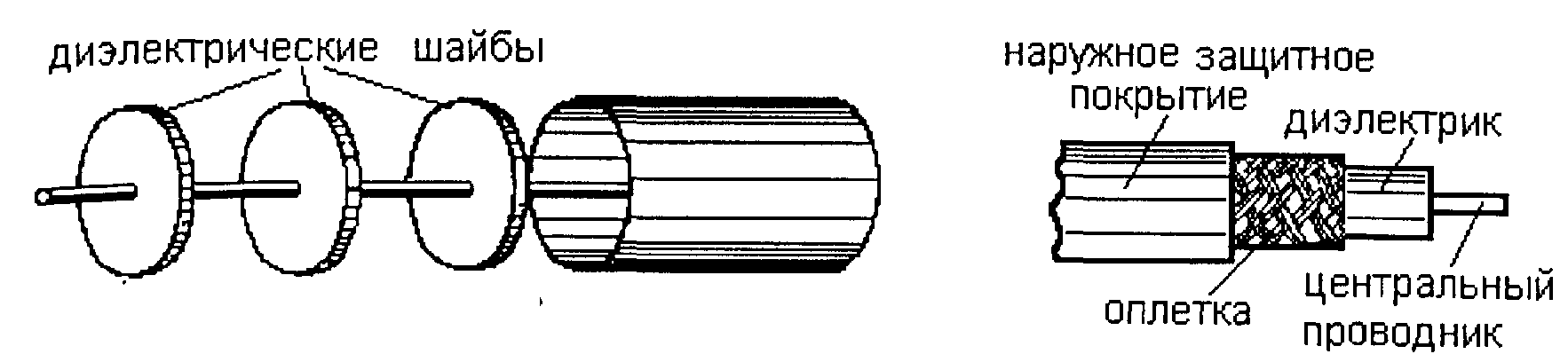
Существует большое многообразие коаксиальных линий как жестких, так и гибких. Последние называются коаксиальными кабелями (рис. 4.2). Экран обычно выполняется из сетки проводников. Центральный проводник бывает одножильным и многожильным. В качестве диэлектрика используются полиэтилен, фторопласт, вспененный полиэтилен. В таблице 4.1 показаны значения коэффициентов замедления , где – относительная диэлектрическая проницаемость заполнения. Для снижения потерь в линии иногда используют вспененный диэлектрик или диэлектрик с воздушными полостями. Снаружи коаксиальный кабель имеет защитную оболочку.

а) б)

Рис. 4.2. Образцы коаксиальных кабелей

а) жесткая коаксиальная линия

б) гибкий коаксиальный кабель

в) образцы коаксиальных кабелей

Таблица 4.1

Коэффициент замедления коаксиальных кабелей

Диэлектрик	ξ
Сплошной полиэтилен	0,66
Фторопласт	0,71
Вспененный полиэтилен	0,78 – 0,89
Спиральный диэлектрик с воздушными полостями	0,87 – 0,96

Поле и параметры волны т в коаксиальной линии

Будем считать, что проводники обладают проводимостью σ→∞, а пространство между ними заполнено идеальным диэлектриком (σ=0) с относительными проницаемостями ε и μ. В коаксиальной линии могут распространяться Т, Е_mn и H_mn волны. Так как у волны Т критическая длина волны λ_кр=∞, то она является основной. Совместим ось z цилиндрической системы координат r, φ, z с осью внутреннего проводника. Радиус внутреннего проводника - а, радиус внешнего проводника - b. Поля электрических Е_mn и магнитных волн H_mn определяются также, как и в круглом волноводе через найденные продольные составляющие Е_z и H_z с учетом дополнительного граничного условия на поверхности внутреннего проводника, что существенно усложняет решение задачи по сравнению с круглым волноводом. Анализ показывает, что волна H₁₁ обладает наибольшей λ_кр, величина которой ограничивает одномодовое распространение основной волны Т. Критическая длина волны H₁₁ приближенно рассчитывается как длина средней окружности между проводниками

(4.1)

Диапазон длин волн одномодового режима работы определяется соотношением .

Параметры волны Т рассчитываются как у плоской однородной волны той же частоты в неограниченном пространстве:

, , , (4.2)

По определению волна Т имеет только поперечные составляющие векторов поля:

,

Волновые уравнения Гельмгольца принимают вид:

(4.3)

Выделив в операторе Лапласа вторую производную по координате z - и произведя дифференцирование в (4.3), получаем уравнения Лапласа

(4.4)

В уравнения (4.4) не входит частота. Из этого следует, что функции и , определяющие структуру поля в поперечных сечениях линии, не зависят от частоты и могут быть найдены на основе решения рассматриваемой задачи при f→0, т.е. достаточно решить статическую задачу для такой же линии. Речь идет о совпадении полей только в поперченном сечении. Электрическое поле Т волны повторяет электростатическое поле в цилиндрическом конденсаторе такого же поперечного сечения. Решение уравнений (4.3, 4.4) с учетом граничных условий определяет поле бегущей волны Т

(4.5)

Амплитуда А имеет запись через максимальную амплитуду электрического поля на поверхности внутреннего проводника, либо через U разность потенциалов между проводниками линии, либо через ток I, вокруг которого возникает магнитное поле:

, , , (4.6)

Чаще используется запись через разность потенциалов между проводниками линии

, (4.7)

где r, z – текущие координаты цилиндрической системы координат;

U – разность потенциалов между проводниками линии;

– коэффициент фазы волны.

Структура силовых линий векторов электромагнитного поля T волны в коаксиальной линии приведена на рис. 4.3. Линии вектора E представляют собой отрезки радиальных линий между проводниками, линии вектора H – концентрические окружности, охватывающие внутренний проводник линии.

Рис. 4.3. Структура поля в коаксиальной линии

На поверхности проводников коаксиальной линии наводятся электрические токи, величина и направление которых определяются тангенциальной составляющей вектора магнитного поля вблизи проводников. Вектор поверхностной плотности распределения наведенных токов равен:

на поверхности центрального проводника

(4.8)

на внутренней поверхности внешнего экрана

(4.9)

Амплитуды токов на проводниках линии определяются умножением плотности токов (4.8, 4.9 с учетом 4.7) на длины контуров сечений внутреннего и внешнего проводника - 2a и 2b соответственно:

(4.10)

Вдоль проводников линии протекают токи одинаковые по величине, но в разных направлениях.

Статический характер поля Т волны в поперечном сечении позволяет ввести понятие напряжения и тока бегущей волны.

Напряжение бегущей волны – синусоидальное напряжение, пропорциональное поперечной составляющей электрического поля волны:

, (4.11)

где – контур в поперечном сечении, соединяющий проводники разных потенциалов.

Продольный ток бегущей волны – синусоидальный ток, пропорциональный поперечной составляющей магнитного поля волны:

, (4.12)

где L – контур в поперченном сечении, охватывающий проводник с одинаковым потенциалом.

Волновое сопротивление линии – величина, определяемая отношением комплексных амплитуд и тока бегущей волны:

(4.13)

Входное сопротивление линии – величина, определяемая отношением комплексных амплитуд напряжения и тока в заданном сечении линии передачи.

Для других типов волн (кроме Т) введение напряжения и тока бегущей волны неоднозначно, а иногда и просто невозможно. Например, поле у электрических, магнитных, гибридных волн имеет вихревой характер и напряжение (4.11) будет зависеть от пути интегрирования. А у волны Н₀₁ (Н_0n) в круглом волноводе продольный ток вообще отсутствует.

Вычислим напряжение, ток и волновое сопротивление у бегущей Т волны

(4.14)

В отличие от характеристического сопротивления, которое определяется параметрами диэлектрика, волновое сопротивление зависит от поперечных размеров линии. Волновое сопротивление является важнейшей технической характеристикой коаксиальной линии и используется при решении задач согласования линий с элементами высокочастотных трактов и устройствами.

Переносимую в коаксиальной линии мощность можно рассчитать, проинтегрировав среднее значение вектора Пойнтинга по поперечному сечению линии, или через ток и волновое сопротивление

:

,

(4.15)

Используется и другая форма записи переносимой мощности (см.4.6,4.7)

(4.16)

Формулу (4.16) можно трактовать как мощность, выделенную на резисторе с сопротивлением ρ, к которому приложено напряжение U.

Предельная мощность связана с напряженностью пробоя воздуха . При полном или частичном заполнении диэлектрика в несколько раз ниже. Это объясняется возможностью теплового пробоя диэлектрика, а также увеличением напряженности электрического поля в небольших (порядка 10^-2…10^-3см) воздушных задорах между диэлектриком и центральным проводником, возникающих даже при самом тщательном изготовлении линии. Напряженность электрического поля в зазоре в выше, чем максимальная напряженность в диэлектрике. И предельная мощность должна быть уменьшена в раз.

Коэффициент затухания волны типа T в коаксиальной линии определяется потерями в диэлектрическом заполнении () и конечной проводимостью центрального проводника и экрана ().

Коэффициент затухания, обусловленный неидеальностью диэлектрика, рассчитывается по формуле

, м^-1 (4.17)

Потери, обусловленные неидеальностью проводников, могут быть определены по формуле

, м^-1, (4.18)

где , – поверхностные сопротивления металла внутреннего и внешнего проводников соответственно.

Формула (4.18) справедлива на высоких частотах при сильном скин- эффекте. Коэффициент затухания имеет минимум при соотношении , что соответствует волновому сопротивлению 77 Ом в линии передачи с воздушным заполнением. На длинах волн λ короче 10см. коэффициент затухания α_м превышает затухание в металлическом волноводе.

Три основные характеристики: передаваемая мощность, затухание и волновое сопротивление линии нелинейно зависят от соотношения радиусов (диаметров).

Из анализа формул следует, что коэффициент затухания имеет минимум при соотношении , что соответствует волновому сопротивлению 77 Ом в линии передачи с воздушным заполнением. Наибольшая электрическая прочность коаксиальной линии имеет место при , что соответствует волновому сопротивлению 30 Ом при воздушном заполнении. Из условий оптимальности характеристик коаксиального волновода берется среднее волновое сопротивление . Следующее стандартное сопротивление , линия с малым затуханием. Для удобства согласования с высокоомными нагрузками в стандартные значения волнового сопротивления коаксиальных кабелей включены так же величины в 100 и 150 Ом. Коаксиальные линии передачи используются от метрового до длинноволновой части сантиметрового диапазонов волн.