Глава 1. Электромагнитные волны в направляющих системах

Лекция 1. Направляющие системы и их основные параметры. Классификация направляемых волн

Направляющие системы и их основные параметры

Кроме электромагнитных волн, свободно распространяющихся в неограниченном пространстве, существуют волны, распространение которых возможно только при наличии каких-либо направляющих элементов (границы раздела сред, металлические трубы, диэлектрические стержни, металлические провода, металлические полоски и экраны и др.). Такие электромагнитные волны называются направляемыми. Совокупность направляемых элементов образует направляющую систему. Направляющие системы служат для передачи энергии электромагнитной направляемой волной от источника (генератора) к потребителю, например от передатчика к антенне, от приемной антенны на вход приемника и т.д. В связи с этим направляющие системы называют также линиями передачи энергии или, более коротко, линиями передачи (фидерами). Линия передачи, у которой поперечное сечение и другие параметры не меняются в продольном направлении, называется однородной.

Общие требования к линиям:

• достаточно высокий КПД передачи электромагнитной энергии (минимальные омические потери);

• характеристики линии должны обеспечивать передачу заданной мощности без электрических пробоев;

• линия передачи не должна обладать антенным эффектом, т.е. излучать электромагнитную энергию;

• в рабочей полосе частот линия должна обладать минимальной дисперсией;

• массогабаритные характеристики линии должны быть возможно минимальными.

На рис. 1.1 изображены поперечные сечения некоторых используемых на практике однородных линий передачи: двухпроводной (а), коаксиальной (б), экранированной двухпроводной (в), симметричной (г) и несимметричной (д) полосковых линий, диэлектрического волновода (е), световода (ж) и полых металлических волноводов: прямоугольного (з), круглого (и) и эллиптического (к).

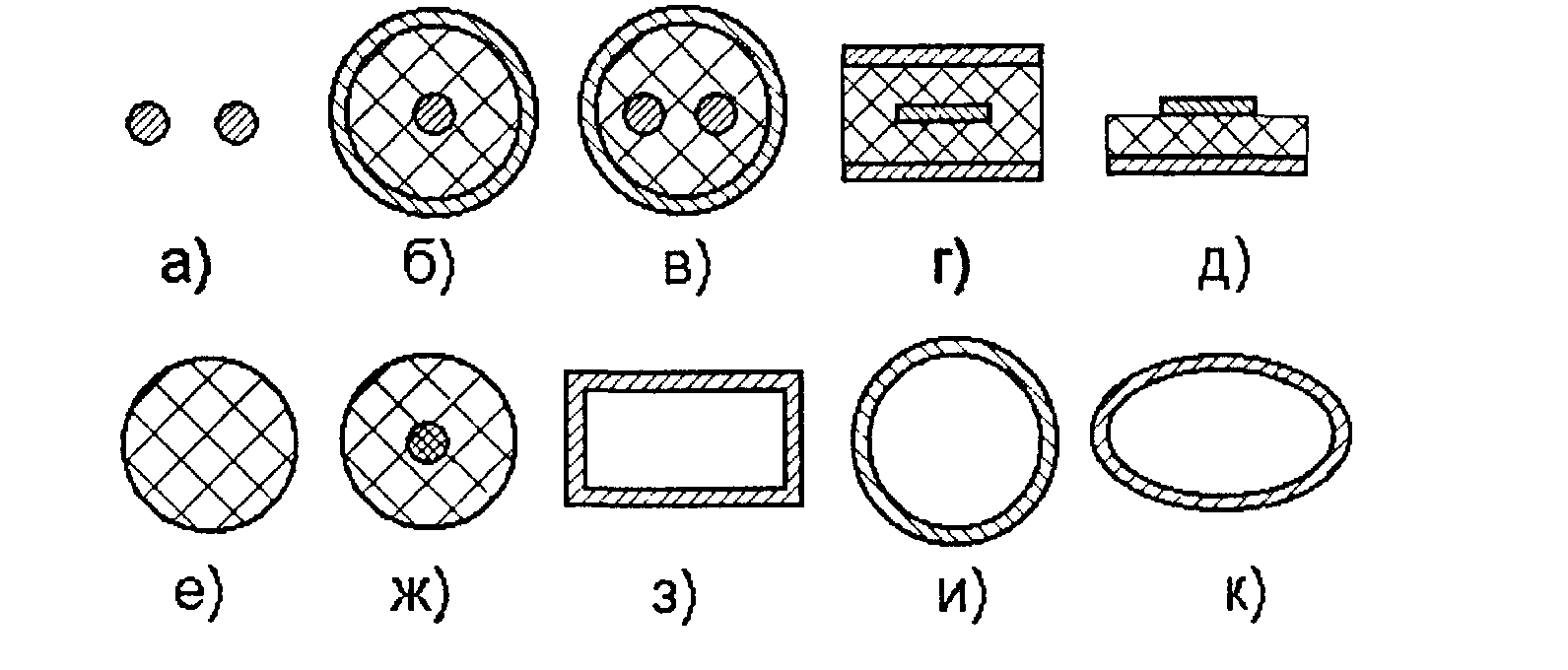
Рис. 1.1

Применение тех или иных линий передачи связано в основном с частотным диапазоном, передаваемой мощностью, наименьшими потерями, с конструктивными особенностями. Существуют большие различия в конструкциях, структурах полей и других параметров разных линий передачи. Однако, процесс передачи электромагнитной энергии во всех линиях одинаков – энергия переносится бегущей электромагнитной волной. Это позволяет выделить общие параметры линий передачи:

1. Тип волны. Передача мощности может производиться вдоль линии с помощью электромагнитного поля определенной конфигурации, представленной далее классификацией направляемых волн.

2. Характеристическое сопротивление. Этот параметр типа волны определяется как отношение составляющих вектора поля и в поперечном сечении линии

3. Погонное затухание.

4. Передаваемая мощность.

5. Длина волны, фазовая и групповая скорости, скорость распространения энергии.

6. Дисперсионная характеристика линии передачи.

Классификация направляемых волн

По структуре поля направляемые волны делятся на поперечные, электрические, магнитные и гибридные.

1. Поперечными волнами, или Т-волнами (Т – первая буква английского слова transverse, что означает поперечный) называются волны, у которых векторы поля и перпендикулярны направлению распространения волн, то есть не имеют продольных составляющих. Для этой волны также используется термин TEM-волна.

2. Электрическими волнами, или E-волнами, называются волны, у которых вектор имеет как поперечные, так и продольную составляющие, а вектор имеет только поперечные составляющие, а продольная составляющая равна нулю. E-волны иногда называют поперечными магнитными или TM-волнами.

3. Магнитными волнами, или H-волнами, называются волны, у которых вектор имеет как поперечные, так и продольную составляющие, а вектор имеет только поперечные составляющие, а продольная составляющая равна нулю. H-волны называют еще поперечными электрическими волнами или TE-волнами.

4. Гибридными, или смешанными волнами называются волны, у которых и вектор и вектор наряду с обязательными поперечными составляющими имеют и продольные составляющие.

Уравнения связи между поперечными и продольными составляющими векторов поля направляемых волн

В случае направляемых волн уравнения Максвелла сводятся к виду, удобному для определения поля в линии передачи и представленному выражениями поперечных составляющих через продольные составляющие.

Рассмотрим произвольную бесконечно протяженную однородную линию передачи, ориентированную вдоль оси z. Будем считать, что линия передачи не вносит потерь, то есть металлические элементы линии идеально проводящие ( = ∞), заполняющий диэлектрик без потерь ( = 0). Такую линию называют идеальной. Занимаемся монохроматическими полями в области, где отсутствует сторонние источники поля.

Линии передачи рассматриваются в декартовой системе координат (x, y, z) или цилиндрической (r, φ, z). Введем обобщенную систему координат , , в которой – координаты, изменяющиеся в поперечном сечении рассматриваемой линии передачи. Так, в декартовой системе координат , , в цилиндрической соответственно , .

Комплексные амплитуды векторов поля волны, бегущей вдоль линии передачи в положительном направлении оси z могут быть представлены в виде

; , (1.1)

где β – коэффициент фазы (постоянная распространения).

Величину β называют еще продольным волновым числом. Фазы векторов поля φ = βz зависят от одной продольной координаты z и постоянны на плоскости z = const, значит волна плоская с уравнением фронта z = const. Амплитуды векторов поля (1.1) зависят от поперечных координат , то есть меняются в плоскости фронта z = const, значит волна неоднородная. Итак, направляемые волны – это плоские неоднородные волны.

Займемся электрическими, магнитными и гибридными волнами, у которых векторы поля (1.1) имеют продольные составляющие. Запишем первое и второе уравнение Максвелла для комплексных амплитуд (1.1)

; (1.2)

. (1.3)

Распишем в обобщенной системе координат через определитель и уравнение (1.2) представим в виде

(1.4)

где – орты вдоль координатных осей ;

– коэффициент Лямэ.

Коэффициенты Лямэ для двух координатных систем:

декартова система ():

_{, , ;}

цилиндрическая система координат (:

, , _;

Запишем два первых скалярных уравнения векторного уравнения (1.4), учитывая дифференцирования по выражений (1.1)

; (1.5)

. (1.6)

К уравнениям (1.5), (1.6) применим принцип перестановочной двойственности и получим два первых скалярных уравнения векторного уравнения (1.3)

; (1.7)

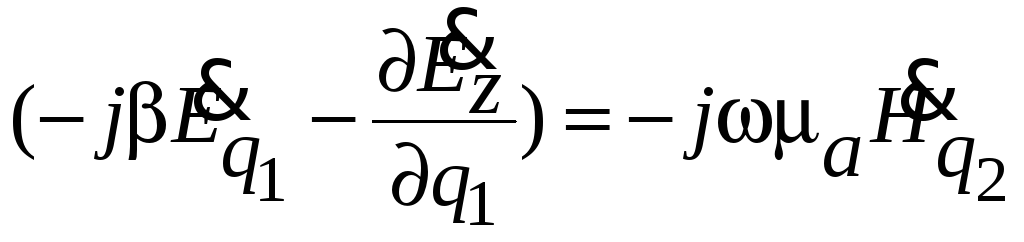. (1.8)

Продолжим преобразование уравнений (1.2), (1.3). Уравнение (1.5) и (1.6) умножаем на , уравнения (1.7) и (1.8) умножаем на . Далее вычитаем из (1.5) уравнение (1.8), а уравнение (1.6) складываем с (1.7), получаем

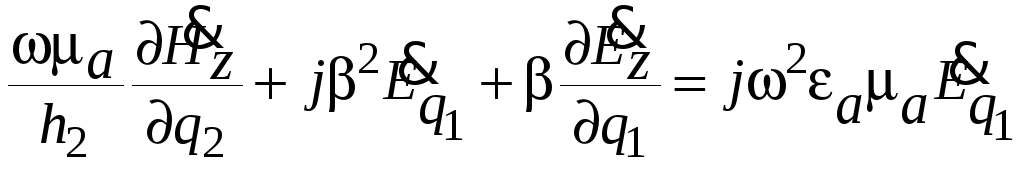; (1.9)

. (1.10)

Величина – это волновое число в неограниченном пространстве. Введем новую величину Величину называют поперечным волновым числом. С учетом величин и из выражения (1.9) получаем первую поперечную составляющую электрического поля , а из выражения (1.10) вторую – .

; (1.11)

. (1.12)

К уравнениям (1.11) и (1.12) применяем принцип перестановочной двойственности и получаем обе поперечные составляющие магнитного поля

; (1.13)

. (1.14)

Уравнения (1.11) – (1.14) связывают поперечные и продольные составляющие векторов поля гибридных направляемых волн. Для магнитных волн в выражениях (1.11) – (1.14) приравниваем нулю , для электрических волн соответственно и получаем искомую связь поперечных и продольных составляющих для этих волн.

Для магнитных волн (,):

(1.15)

Для электрических волн ():

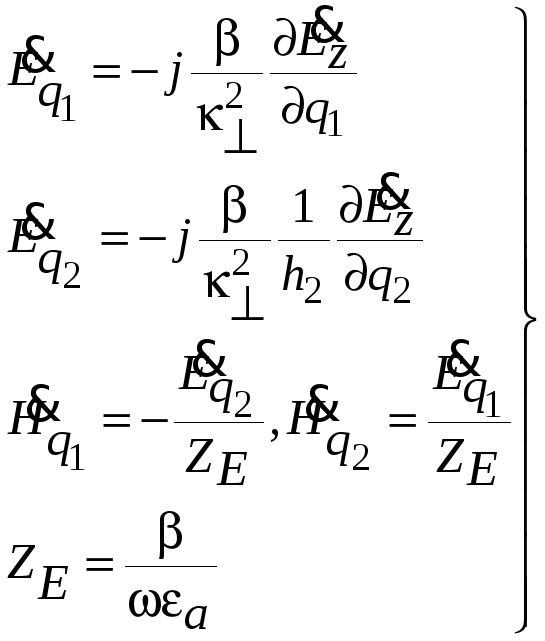(1.16)

В системах (1.15), (1.16) использована связь поперечных составляющих электрического и магнитного полей через характеристическое сопротивление. При анализе системы уравнений (1.11) – (1.16) следует отметить:

1. Поперечные составляющие векторов поля синфазны (противофазны), а это значит, что мнимая часть продольной составляющей комплексного вектора Пойнтинга равна нулю и вся энергия распространяется вдоль идеальной линии передачи.

2. Поперечные составляющие сдвинуты по фазе относительно продольных на величину (наличие в выражениях (1.11) – (1.16)).

3. Для электрических, магнитных и гибридных волн поперечное волновое число отлично от нуля .

4. Для поперечных -волн, у которых отсутствуют продольные составляющие векторов поля, не может быть , поэтому принимается условие .

Таким образом, для определения поля электрических, магнитных и гибридных волн достаточно найти составляющие и путем решения однородных уравнений Гельмгольца

, (1.17)

и подчинить их граничным условиям в рассматриваемой линии передачи, а для вычисления поперечных составляющих использовать равенства (1.11) – (1.16).

Лекция 2. Условие распространения направляемых волн. Параметры электрических, магнитных, гибридных и поперечных электромагнитных волн

Условие распространения направляемых волн

Коэффициент фазы (постоянная распространения) направляемой волны равен

, (1.18)

где – коэффициент фазы (постоянная распространения) плоской однородной волны с частотой , свободно распространяющейся в неограниченной среде без потерь;

– поперечное волновое число для направляемой волны с частотой .

Постоянная зависит от формы и размеров поперечного сечения линии передачи и от типа распространяющейся волны, но не зависит от частоты. Так как , то в зависимости от частоты подкоренное выражение в (1.18) может быть положительным при равным нулю при или отрицательным при .

Если частота такова, что коэффициент фазы – действительное число и фазы составляющих векторов поля (оператор бегущей волны в выражениях (1.1)) в фиксированный момент времени линейно зависят от координаты , что является признаком распространения направляемой волны вдоль оси , сопровождаемое переносом энергии вдоль линии передачи.

Если частота такова, что , то подкоренное выражение в (1.18) оказывается отрицательным и тогда в выражениях (1.1) коэффициент фазы будет равен . Оператор бегущей волны переходит в затухающую экспоненту и амплитуды составляющих векторов поля (1.1) экспоненциально убывают вдоль оси . Фазы составляющих векторов поля в этом случае не зависят от координаты : поле имеет характер стоячей волны и экспоненциально уменьшается вдоль оси . Переноса энергии вдоль линии не происходит.

В третьем случае коэффициент фазы . Такой режим называется критическим. Частота , определяемая из условия , называется критической частотой:

. (1.19)

Длина волны, соответствующая этой частоте вычисляется по известной формуле через фазовую скорость

.

С учетом (1.19) определяем критическую длину волны – наибольшую длину волны, превышая которую волна может передаваться по линии

. (1.20)

С введением критических параметров и представим в следующем виде:

. (1.21)

Коэффициент фазы является действительной величиной, то есть поле (1.1) представляет собой распространяющуюся волну, только при выполнении условия

. (1.22)

Неравенство (1.22) можно представить и в виде

. (1.23)

Неравенство (1.22), а также неравенство (1.23) называют условием распространения направляемых волн в линиях передачи. Таким образом, электрические, магнитные и гибридные волны могут распространяться только на частотах, превышающих критическую частоту. Значение зависит от формы и размеров поперечного сечения линии и от типа направляемой волны. На рис. 1.2 приведены частотные зависимости постоянных распространения свободной и направляемой волн.

Рис. 1.2. Частотная зависимость коэффициентов фазы

Для поперечных - волн поперечное волновое число , отсюда и , эти направляемые волны не имеют частотного ограничения и могут распространяться вдоль линий на любых частотах.