ЭД и РРВ Лекции1-24 И.П / Лекция 7 Круглый волновод

Глава 3. Круглые волноводы

Лекция 7. Электрические и магнитные волны в круглом волноводе

Круглый металлический волновод-это линия передачи в виде металлической трубы круглого поперечного сечения радиуса а. Задача определения поля в круглом волноводе решается в той же общей постановке, что и в прямоугольном волноводе: стенки волновода обладают бесконечной проводимостью, а заполняющая его среда - идеальный диэлектрик с параметрами  и .. Волновод бесконечно протяжённый (чисто бегущая волна). Поле монохроматическое. Будем считать, что источник находится за пределами рассматриваемой части линии передачи и создаваемая им волна распространяется вдоль оси z. Используемая цилиндрическая система координат и радиус а поперечного сечения волновода показаны на рис.3.1.

Рис. 3.1. Круглый волновод

В круглом волноводе с однородным диэлектрическим заполнением могут распространяться магнитные волны и электрические волны (m = 0,1,2,... , n = 1, 2, 3, ...) и невозможно существование Т волны. Для определения поля электрических и магнитных волн необходимо решить в цилиндрической системе координат однородные волновые уравнения Гельмгольца для продольных составляющих векторов поля. Как и в прямоугольном волноводе используется метод разделения переменных, согласно которому искомое решение представляется в виде произведения двух функций, каждая из которых зависит только от одной переменной (r или φ). Полученное решение подчиняем граничным условиям: на идеально проводящих стенках волновода касательная составляющая вектора напряженности электрического поля равна нулю. Приведем решение в конечном виде.

Электромагнитное поле распространяющейся волны имеет компоненты:

,

,

,

, , , (3.1)

где - функция Бесселя m-го порядка от аргумента ;

а- радиус волновода;

- n-й корень функция Бесселя m-го порядка (n=1,2,…);

- первая производная функции Бесселя m-го порядка от аргумента;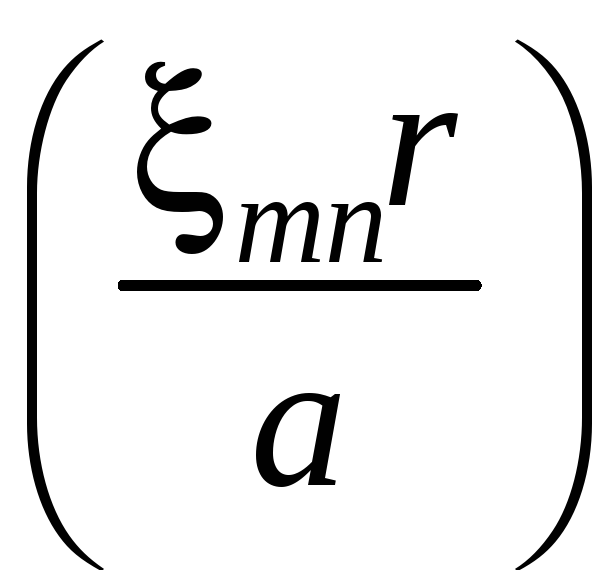

m- индекс, принимающий числовые значения

Электромагнитное поле распространяющейся волны типа имеет компоненты:

,

,

,

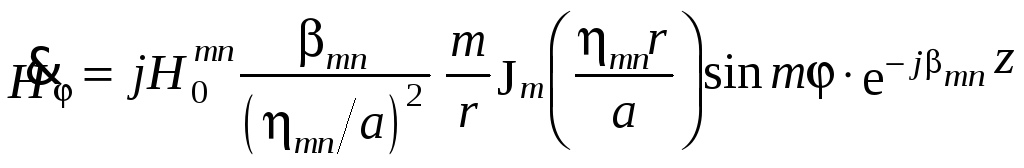, , , (3.2)

где - функция Бесселя m-го порядка от аргумента ;

– n-й корень первой производной функция Бесселя m-го порядка (n=1,2,…);

- первая производная функции Бесселя m-го порядка от аргумента.

Вкратце познакомимся с функциями Бесселя. Аналитически функция Бесселя выражается через бесконечный сходящийся ряд достаточно сложной структуры. В цилиндрической системе координат функция Бесселя играют такую же роль, что и тригонометрические функции в прямоугольной системе координат (в асимптотике при больших аргументах) они выражается через косинус определенного аргумента. Но функция Бесселя имеет существенные отличия от гармонических функций:

1. Функция Бесселя в отличие от гармонических не является периодической. Это непериодическая, непрерывная колеблющаяся функция с монотонно убывающей амплитудой с ростом аргумента.

2. Все функции Бесселя в нуле равны нулю, за исключением J₀(0)=1.

3. Функция Бесселя и её производные имеют бесконечное множество корней. Корни – это значения аргумента, при которых функция Бесселя или ее производная обращается в нуль. Введем обозначения корней: J_m(ξ_mn)=0 , где ξ_mn – n-й корень функции Бесселя m-ого порядка (n=1,2….). Первая производная функции Бесселя по аргументу обозначена в (3.1),(3.2) штрихом и обращается в нуль (η_mn)=0, где η_mn-n корень первой производной функции Бесселя m-ого порядка (n=1,2….). Функции Бесселя нулевого, первого и второго порядков показаны на рис.3.2.

Рис. 3.2 Функции Бесселя нулевого, первого и второго порядков

В таблицах 3.1 и 3.2 со справочными целями приведены значения некоторых корней функций Бесселя и их первых производных.

Таблица 3.1

Значения корней функций Бесселя J_m(_mn)

	n = 1	n = 2	n = 3
m = 0	2,405	5,520	8,654
m = 1	3,832	7,016	10,173
m = 2	5,136	8,417	11,620
m = 3	6,380	9,761	13,015

Таблица 3.2

Значения корней первой производной функций Бесселя J_m^’(_mn)

	n = 1	n = 2	n = 3
m = 0	3,832	7,016	10,174
m = 1	1,841	5,331	8,536
m = 2	3,054	6,705	9,965
m = 3	4,200	8,017	11,403

Индексы m и n означают: m означает число вариаций поля по угловой координате φ, а n - число вариаций поля по радиальной координате r. В частном случае m=0 амплитуды векторов электромагнитного поля не зависят от угловой координаты, структура поля обладает осевой симметрией: подобные типы волн называют симметричными.

Критические длины волн типа находят по общей формуле

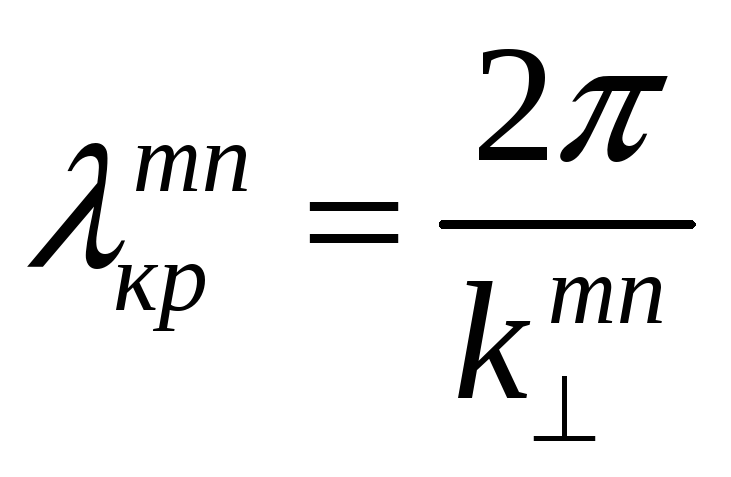
и они вычисляются

(3.3)

Соответственно и для волн типа

(3.4)

Волны Н_1n и Е_0n имеют равные критические длины волн и будут вырождены.

Конкретный тип волны в волноводе будет распространяться при условии:

, ,

где – критическая длина волны данного типа колебания;

– критическая частота.

При вычисленном параметре основные параметры волн в круглом волновода , , , , , , , рассчитываются по тем же формулам, что и в прямоугольном волноводе.

Коэффициент затухания, обусловленный потерями в металлических стенках круглого волновода, вычисляется следующим образом:

• для волн типа

, (3.5)

• для волн типа

, . (3.6)

Соотношение между критическими длинами волн нескольких первых типов показано на рис.3.3

Рис. 3.3. Значения λ_кр типов волн в круглых волноводах

Волны H₁₁, E₀₁ и H₀₁ в круглом волноводе

В круглых волноводах чаще других используются волны типов H₁₁, E₀₁ и H₀₁. Волна Н₁₁ обладает наибольшей λ_кр

(3.7)

и является основной волной в круглом волноводе.

Рабочий диапазон частот в одномодовом режиме определяется условием

. (3.8)

Поле бегущей волны Н₁₁ определяется выражениями (3.2) при подстановке индексов волны m=1 и n=1

,

,

,

, , . (3.9)

Фазы составляющих векторов поля по прежнему просты φ=β₁₁z и они линейно меняются с изменением координаты z. Амплитуды составляющих векторов поля зависят от угловой координаты φ (sin φ, cos φ) и особенно сложно от радиуса (1/r и функции Бесселя и 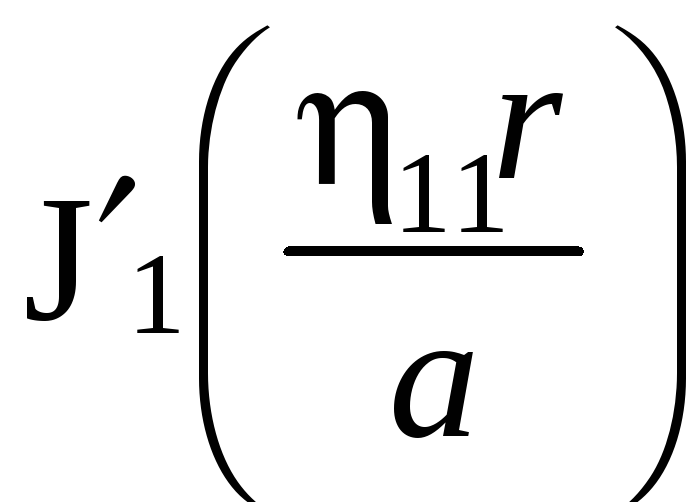). Основные параметры волны вычисляются по общим формулам при известном значении λ_кр=3,41а.

Картина силовых линий вектора поля Е и Н основной волны показана на рис.3.4. в трех сечениях.

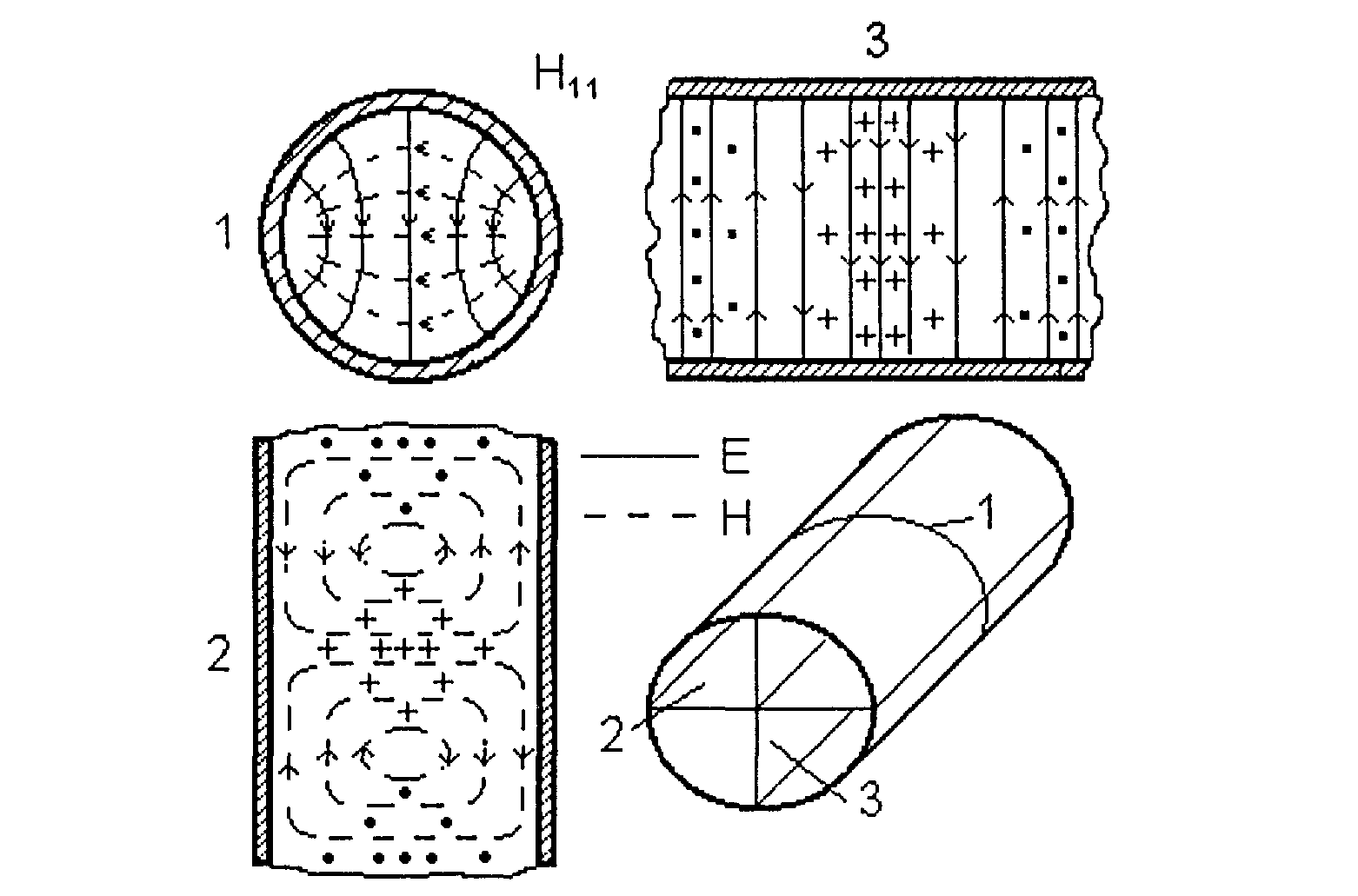
Рис.3.4 Структура поля волны Н₁₁

В поперечном и двух продольных сечениях структура поля волны Н₁₁ близка к структуре поля волны Н₁₀ в прямоугольном волноводе. При деформации прямоугольного сечения волновода к круглому сечению, волна Н₁₀ плавно преобразуется в волну Н₁₁. Плавный переход от прямоугольного волновода к круглому служит возбудителем волны Н₁₁ (рис.3.5) .

Рис.3.5 Последовательные этапы деформации прямоугольного волновода

При распространении волны Н₁₁ на стенках волновода наводятся переменные токи проводимости. Силовые линии вектора поверхностной плотности наведенных токов показаны на рис. 3,5(их картина также напоминает картину поверхностных токов на стенках прямоугольного волновода на волне Н₁₀).

Рис. 3.5 Распределение токов на волне Н₁₁

Волна основного типа в круглом волноводе обладает существенным недостатком – неустойчивостью поляризации поля. В силу круговой симметрии контура стенок волновода в нем может распространяться волна с любой ориентацией вектора Е в поперечном сечении линии, что приводит к повороту структуры поля. Например, если на входе волноводной системы волна поляризована так, как показано на рис 3.6, то под влиянием различных случайных деформаций волноводной линии волна на выходе имеет уже другое направление плоскости поляризации. Поляризационная неустойчивость – это следствие совершенной симметрии круглого волновода.

Рис.3.6 Поляризационная неустойчивость волны

Поскольку приемные устройства работают, как правило, на волну с определенной поляризацией, то поляризационная неустойчивость волны Н₁₁ препятствует использованию круглых волноводов с Н₁₁ в качестве линии передачи. Поляризационная неустойчивость снимается эллиптическим поперечным сечением, т.е. эллиптическим волноводом. Отметим тут же, что все симметричные волны поляризационно устойчивы.

Волна Е₀₁ – это следующая по λ_кр волна. Волна типа E₀₁ является наинизшей из симметричных волн и находит применение во вращающихся сочленениях. Критическая длина волны .

Для обеспечения возможности распространения волны типа E₀₁ и исключения волн высших типов необходимо выполнить условие , где - критическая длина волны ближайшего высшего типа H_21, или в частотах

(3.10)

При выполнении этого условия кроме волны E₀₁ в волноводе может распространяться волна основного типа H₁₁.

Поле бегущей волны Е₀₁ определяется из выражений (3.1) при m=0 и n=1

,

,

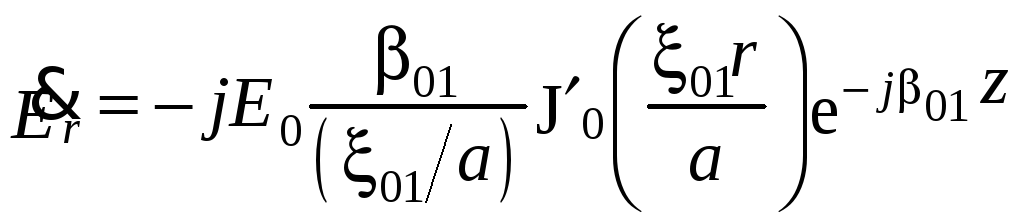(3.11)

Основные параметры вычисляем по общим формулам при λ_кр=2,61а.

Волна имеет простейшую структуру поля (рис.3.7)

Рис. 3.7 Структура поля волны E₀₁

Одна составляющая магнитного поля Н_φ , тангенциальная стенкам волновода, определяет только продольные поверхностные токи на волне Е_01, равномерно распределенные по периметру волновода. Следует отметить, что у всех электрических волн типа Е_mn токи только продольные.

Определенные перспективы имеет передача электромагнитной энергии по круглому волноводу с помощью волны H₀₁. Это обусловлено тем, что с повышением частоты затухание волны этого типа уменьшается. Критическая длина волны . Волна типа H₀₁ распространяется, если выполняется условие . При этом в волноводе могут распространяться и волны H₁₁, E₀₁, H₂₁. Таким образом, при использовании волны типа H₀₁ необходимо принимать специальные меры к чистоте возбуждения волны H₀₁.

Поле бегущей волны Н₀₁ определяется выражениями (3.2) при подстановке индексов волны m=0 и n=1. Основные параметры вычисляются по общим формулам при .

Симметричная волна Н₀₁ имеет простую структуру поля (рис.3.8). Волна Н₀₁ имеет одну составляющую магнитного поля Н_z тангенциальную стенкам волновода, которая и определяет только поперечные поверхностные токи на волне Н₀₁ (рис.3.9).

Рис. 3.8 Структура поля волны Н₀₁

Рис. 3.9 Распределение токов на волне Н₀₁

Волна (также как и волны , n- любое целое число) обладает эффектом, так называемого, аномального затухания, когда в отличие от других типов волн затухание этой волны уменьшается с ростом частоты. Это объясняется структурой поля волны Н₀₁. С ростом частоты Н_z уменьшается, т.е. уменьшается поток вектора Пойнтинга в стенки, и потери уменьшаются (рис.3.10).

Рис. 3.10 Зависимость коэффициента ослабления α_м (в дБ/м) от частоты для волн H₀₁, E₀₁ и в случае круглого медного волновода радиуса 25,4 мм.

Круглые волноводы в настоящее время в качестве линий передачи на большие расстояния не используются. Основное их назначение – применение в качестве элементов в различных устройствах СВЧ, например, во «вращающихся узлах волноводных трактов».

Контрольные вопросы

1. Перечислите преимущества и недостатки волноводных линий передачи

2. Нарисуйте графики изменения длины волны в волноводной линии от частоты. Чем можно объяснить такое поведение графиков?

3. Определите частотный диапазон работы прямоугольного и круглого волноводов на основном типе колебаний?

4. Что такое ортогональность типов волн в волноводах?

Литература

1. Соловьянова И.П., Наймушин М.П. Теория волновых процессов. Электромагнитные волны: учебное пособие. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2005. 132 с.

2. Петров Б.М. Электродинамика и распространение радиоволн / Б.М. Петров. М.: Горячая линия-Телеком, 2003. 558 с.

3. Вольман В.И. Техническая электродинамика/ В.И. Вольман, Ю.В. Пименов, А.В. Муравцев. М.: Связь, 2000. 480 с.