Если погрешность с произвольным законом распределения имеет [1]

энтропию Н(X_as), то поле допуска можно в общем случае выразить

(10)

 =  ½ exp H (X_as).

• П.В. Новицкий дает следующее определение энтропийной погрешности: "Энтропийным значением погрешности считается значение погрешности с равномерным законом распределения, которое вносит такое же дезинформационное действие, что и погрешность с данным законом распределения вероятностей". Следует отметить, что наибольшей энтропией обладает нормальный закон распределения, поэтому коэффициент K для нормального закона будет иметь максимальное значение K = 2,07.

Для равномерного закона распределения.

Энтропийную погрешность можно вычислить, зная закон распределения погрешности Р(X_as). При оценке точности измерительных устройств или измерений мы не знаем этого закона, а имеем лишь некоторое число n конкретных значений случайной величины x, подчиняющихся этому закону. По результатам измерений можно построить гистограмму, которая с той или иной степенью приближения отражает истинный закон распределения Р (Х_аs). Гистограмма строится следующим образом: весь диапазон значений x_i разбиваем на m интервалов с шириной d_i, так, чтобы в один интервал попадало не менее 2-3 результатов, над каждым отрезком оси абсцисс, изображающим интервал, строится прямоугольник, высота которого пропорциональна плотности вероятности (рис. 1.3).

, (11)

где n_i -- число результатов, попавших в i интервал.

Гистограмма позволяет определить основные характеристики погрешностей.

• При ассиметричных гистограммах (Гауссовский закон распределения не выполняется) определение вероятнейшего результата измерения может производиться по центру тяжести (медианный центр), максимуму вероятности или как центр размаха [1]. Если гистограмма имеет смещённый максимум, то для оценки используется медианный центр, если имеет ярко выраженный максимум – оценка производится по максимуму вероятности. При антимодальном распределении – возможно использовать центр размаха.

Среднеквадратическое значение определяется как половина максимального отклонения от вероятнейшего значения.

Данный метод требует производства 130 -500 измерений, так как закон распределения погрешности достаточно точно определяется большой выборкой случайных величин. Измерения по данной методике рекомендуется производить в случае ответственных измерений, например, при аттестации вновь разработанных измерительных приборов.

При этом возникает необходимость внедрения ЭВМ для полной автоматизации измерений, вычислений и получения гистограммы.

Если ширина всех столбцов одинакова d_i= d, энтропийное значение погрешности равно [2]:

(12)

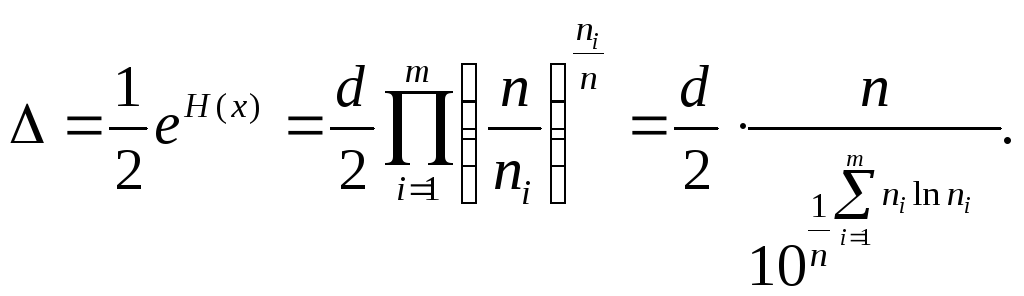
		ВВЕДИТЕ ДАННЫЕ ДЛЯ РАСЧЕТА
		Ширину интервала	1
		число интевалов	9
0	0,5	Число попаданий в 1 интервал	0
1	1,5	Число попаданий в 2 интервал	0
2	2,5	Число попаданий в 3 интервал	0
3	3,5	число в 4 интервал	68
4	4,5	число в 5интервал	89
5	5,5	число в 6интериал	125
6	6,5	число в 7интервал	254
7	7,5	число в 8интервал	284
8	8,5	число в 9интервал	12
	Рассчитанные значения
Число измерений			832
Среднеарифметическое			6,26
Среднеквадратичное отклонение			1,29
Энтропийная погрешность			2,28343
Коэффициент энтропийной погрешности			1,77468

Рис. 1.3 .Обработка результатов измерений ЭВМ

В технических измерениях энтропийная погрешность

   2,0,

Энтропийное значение погрешности по международной терминологии относится к неопределенности типа В.

9. Характеристики измерительных приборов

Погрешности измерительных приборов характеризуются не по отдельным точкам, а сразу во всем рабочем диапазоне. В простейшем случае, когда абсолютная величина погрешности остается постоянной во всем рабочем диапазоне прибора, такой характеристикой является приведенная погрешность ( = const), выраженная (13).

Приведенной погрешностью называется отношение предельной допускаемой абсолютной погрешности средства измерения к условно принятому значению величины, определяющей ширину диапазона. Условно принятое значение величины называют нормирующим значением, за которое часто принимают верхний предел измерений равный предельному значению шкалы прибора X_max или ширине диапазона измерений:

(13)

Общая погрешность прибора обусловливает его класс точности, который обозначают числом, совпадающим с приведенной погрешностью, выраженной в процентах. Для обозначения классов точности установлен следующий ряд чисел: 1; 1,5; 2; 2,5; 5; 6, которые умножаются на, где п = 1, 0, -1, -2. Например, прибор с приведенной погрешностью = ± 0,5% обозначается как прибор класса 0,5.

• Следует отметить, что получение относительной погрешности (6а), равной классу точности, возможно только при измерении величины, равной X_max, во всех остальных случаях относительная погрешность получается тем больше, чем ближе к началу шкалы находится отсчет. Поэтому измерения такими приборами рекомендуется производить в последней трети шкалы прибора. Примером таких приборов могут служить магнитоэлектрические приборы, основным источником погрешностей которых является сухое трение в осях подвижной рамки преобразователя.

В более сложных приборах наряду с постоянной (аддитивной) составляющей погрешности присутствует составляющая пропорциональная измеряемой величине (мультипликативная составляющая). Если представить функцию преобразователя прибора линейной, то распределение поля допуска вдоль шкалы прибора будет иметь вид, представленный на рисунке 1.4 а. Для задания такой погрешности прибора пользуются двухчленной формулой (рис. 1.4 б):

 =  (₀+_Sх), (14)

где ₀ -- аддитивная составляющая,

_S -- относительная погрешность чувствительности.

. (14а)

При отсутствии входной величины погрешность прибора определяется только аддитивной составляющей, поэтому последняя получила название погрешности нуля.

В соотношение (14а) удобно ввести конечное значение шкалы прибора Х_к, -- наибольшее значение измеряемой величины, указанной на шкале:

.

Обозначив и , где g- сумма мультипликативной и аддитивной составляющей погрешности :

(14б)

при

В конце шкалы погрешность составляет сумму аддитивной и мультипликативной составляющей по абсолютной величине, а в начале – только аддитивной. В средине шкалы относительная погрешность составит сумму мультипликативной составляющей и удвоенной аддитивной. Относительная погрешность к началу шкалы возрастает.

• Когда погрешность прибора задана в соответствии с этой формулой, то его класс точности выражается дробью g/e. Например, если прибор характеризуется b_макc= ±[0,1 + 0,06((x_k/x)-1)]%, то его класс точности 0,1/0,06.

Рис. 1.4. Погрешность прибора в диапазоне при двухчленной формуле

а-- поле допуска; б—абсолютная погрешность прибора

При большом рабочем диапазоне прибора поле допуска вдоль шкалы прибора может изменяться более сложным образом. Это может быть учтено добавлением в формулу членов с переменной в более высокой степени.

Однако практически трехчленные формулы применяются очень редко.

Определим основные понятия, которые используются для характеристики измерительных устройств, имеющих функцию преобразования y= f(x).

1. Чувствительность средства измерений определяется отношением изменения выходного сигнала этого средства к вызывающему его изменению измеряемой величины.

Абсолютная чувствительность средства измерения, которая для измерительного преобразователя является крутизной характеристики преобразователя, определяется по формуле

,

где x -- приращение входной величины,

y -- приращение соответственно выходной величины.

Под порогом чувствительности понимается значение входной величины, равное абсолютной величине погрешности нуля прибора.

2. Диапазон показаний средства измерений определяется как область значений шкалы прибора, ограниченная начальным и конечным значением шкалы. Диапазон средства измерений, определяющий область значений величины, в пределах которой нормированы погрешности средства измерений - - является рабочим. Пределы измерений в паспорте прибора задаются в единицах той физической величины, для измерения которой он предназначен. Для сравнения различных приборов пользуются понятием полного или динамического диапазона, который характеризуется отношением

где X_max -- максимальное значение длины шкалы;

₀ -- погрешность нуля.

3. Разрешающая способность характеризует способность прибора различать два близлежащих значения измеряемой величины и по определению разрешение средства измерений () -- это характеристика средства измерений, определяется наименьшим интервалом времени между отдельными импульсами или наименьшими расстояниями между значениями, которые фиксируются прибором раздельно. При информационном подходе разрешающую способность определяют как число достоверно различимых градаций измерения во всем диапазоне прибора (рис. 1.5). Согласно этому определения число квантов измеряемой величины вписывающихся в полосу неопределенности прибора по всей длине рабочего диапазона прибора, зависит от ширины поля допуска вдоль шкалы и длины диапазона. Это особенно важно в цифровых приборах.

Квантование происходит при переходе от аналоговой величины к дискретной. В цифровых преобразователях (АЦП рис. 2.11б) возникает погрешность квантования или дискретизации, равная аддитивной составляющей  _0, которая определяет число квантов измеряемой величины N. Эта погрешность возникает при случайном во времени расположении счетных импульсов относительно временного интервала Т.

Максимальное значение погрешности 1 счетный импульс, а относительное значение  1/ N , где N – число импульсов.

При одном случайном факторе (передний фронт интервала синхронизирован со счетным импульсом) закон распределения погрешности дискретизации – равномерный , а при двух случайных факторах (для переднего и заднего фронта) – закон распределения треугольный (рис. 1.1).

Рис. 1.5 . Разрешающая способность прибора

4. Точность средства измерения это характеристика качества средства измерений, отражающая близость его погрешности к нулю. Под точностью прибора обычно принимают величину обратно пропорциональную погрешности прибора.

5. Быстродействие или время измерения - время зависимое от скорости протекания переходных процессов, необходимое для производства измерения с точностью, указанной в паспорте, определяет динамическую погрешность.

6. Среди метрологических характеристик следует дополнительно рассмотреть полное входное сопротивление поскольку возникает систематическая ошибка при включении прибора в цепь. При последовательном включении амперметров режим работы электрической цепи будет мало изменяться когда малое входное сопротивление, при параллельном подключении вольтметров – когда большое входное сопротивлениие. В общем случае потребляемая мощность по входной цепи должна быть минимальна, но в этом случае возрастает влияние наводок.

1. пределы измерений приборов (по входу);

2. номинальные значения мер;

3. диапазон рабочих частот;

4. характеристики систематической составляющей погрешности;

5. характеристики случайной составляющей погрешности, в частности, пределы допускаемого среднеквадратического отклонения;

6. характеристики полной погрешности, в частности, пределы допускаемой погрешности;

7. полное входное сопротивление;

8. динамические характеристики: амплитудно-частотная, переходная и фазочастотная характеристика;

9. функции влияния, представляющие собой зависимость метрологических характеристик от изменения влияющих величин или неинформативных параметров входного сигнала.

По стандарту РФ все радиотехнические приборы разделены на 20 подгрупп , обозначаемых буквами русского алфавита. Основные из них:

А – измерители силы тока,

В – измерители напряжения,

Г – генераторы ,

Д – аттенюаторы,

Е – измерители параметров цепей с сосредоточенными постоянными,

М – измерители мощности,

П – измерители напряженности поля и радиопомех,

Р– измерители параметров элементов с распределёнными постоянными

С – приборы для исследования формы сигнала,

Ф – измерители фазовых сдвигов,

Ч – измерители частоты.

Номер, следующий за буквой, определяет способ измерения, а следующий – номер конструкции.

Все радиоизмерительные приборы подразделяются:

• Показывающие – оператор считывает результат.

• Регистрирующие – результат фиксируется и запоминается.

• Интеллектуальные – результат измерения используется в автоматических системах и ЭВМ для автоматизации процессов после соответствующей обработки информации.

Последний вид измерений находит всё большее применение в связи с автоматизацией производственных процессов и иногда называют компьютерные измерения, однако компьютер только обрабатывает информацию, полученную при измерении.

26