1.6. Среднеквадратическая ошибка среднего арифметического

Производя ряд равноточных измерений, мы за результат принимаем среднее арифметическое, как вероятнейшее значение результата измерений. Определим зависимость между среднеквадратической ошибкой отдельного измерения и среднего арифметического. Среднее арифметическое можно рассматривать как функцию

А = (1/n)x₁ + (1/n)x₂ + (1/n)x₃ +…+ (1/n)x_n.

Используя формулу для косвенных измерений, получим

²_А = (1/n)²²x₁ + (1/n)²²x₂+….+ (1/n)²²_,

так как измерения производились одним и тем же прибором в одних и тех же условиях, то

x₁  x₂  x_n = _0;

(5)

• Среднеквадратическая ошибка среднего арифметического равноточных измерений меньше среднеквадратической погрешности отдельного измерения в 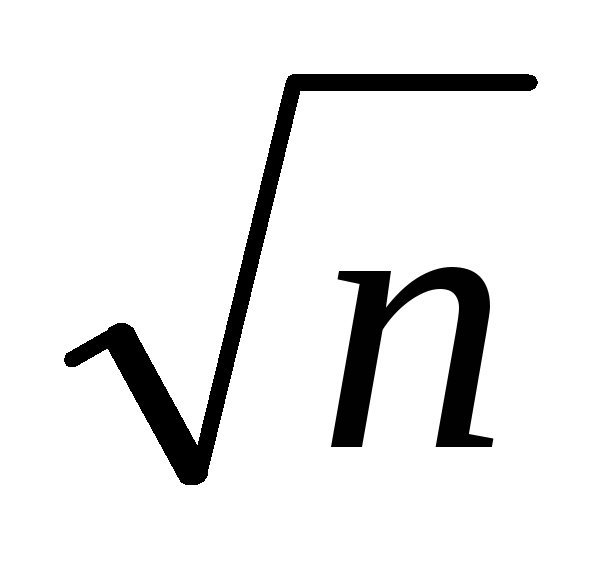раз.

На первый взгляд создается впечатление, что, увеличивая беспредельно число измерений n, мы можем увеличивать беспредельно точность измерения, однако в действительности следует иметь в виду, что кроме случайной составляющей погрешности всегда имеет место некоторая неисключенная систематическая составляющая. Свойства систематических погрешностей отличны от свойств случайных и увеличением числа результатов измерений их исключить нельзя. Кроме того, для производства множества измерений необходимо достаточно большое время, в течение которого условие равноточности измерений может потерять силу, поэтому обычно число измерений не превышает десяти.

1.7. Определение поля допуска ( неопределённость типа а)

В процессе измерения важно не только определить вероятнейшее

значение физической величины, но и указать с какой точностью это значение найдено. Точность измерения характеризуется обычно полем допуска или иначе доверительным интервалом. Доверительным называют интервал, который с заданной вероятностью включает в себя неизвестный параметр. Зависимость между доверительным интервалом и вероятностью наглядно определяется плотностью распределения случайной погрешности. Чем шире доверительный интервал, тем больше площадь, вырезаемая этим интервалом из кривой распределения плотности вероятности, тем больше вероятность, что истинное значение измеряемой величины лежит в этом интервале. При известном законе распределения плотности вероятности, для того чтобы задать доверительный интервал, необходимо задать доверительную вероятность. Только в случае равномерного закона распределения границы доверительного интервала выражены четко (рис. 1.2), равновероятно нахождение погрешности в пределах -  до + , а меньше и больше практически не встречаются. В этом случае можно говорить о поле допуска .В случае распределения погрешностей с плавными спадами плотности вероятности по мере увеличения погрешности (нормальный закон) указать поле допуска простым логическим рассуждением невозможно.

Рис. 1.2 . Закон равномерного распределения

а -- график плотности вероятности; б -- график функции

В некоторых теоретических работах рекомендуется поле допуска

определять по "правилу трех сигм". Эта рекомендация приемлема только при высокоточных измерениях, когда систематическая ошибка отсутствует, а среднеквадратическая ошибка  находится по несколько десяткам результатов измерений. Только в этом случае возможно задавать поле допуска с «перестраховочной» доверительной вероятностью 0,997. Если же при технических измерениях число измерений невелико, среднеквадратическая ошибка находится с малой точностью, так как фактически пользуются оценкой величины ' , которая так же является случайной величиной, погрешность в определении поля допуска не будет соответствовать столь высокой доверительной вероятности. В этом случае вместо нормального закона распределения случайной погрешности применяется закон распределения Стьюдента, а поле допуска определяется по формуле

(6)

где ' -- оценка среднеквадратической погрешности по малому числу n измерений;

t -- коэффициент Стьюдента.

Для определения коэффициента t по заданному числу измерений и доверительной вероятности q пользуются таблицами, которые составлены по результатам вычисления распределения Стьюдента (приложение ).

Графическое изображение распределения Стьюдента отличается от нормального более пологими крыльями, но при увеличении числа результатов измерений это различие уменьшается и уже при n>30 им можно пренебречь. Приведем примеры применения этой таблицы.

• Пусть среднее арифметическое из 5 измерений будет 31,2. Средняя квадратическая ошибка, определенная из этих 5 измерений, равна 0,24.

Для условий задачи определим поле допуска при доверительной вероятности р = 0,95. По таблице находим при n=5 t=2,8. По формуле ( 6 ) определим поле допуска.