5. ФОРМУЛЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ

5. ФОРМУЛЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ

6.1. Плоскость

5.1. Плоскость в пространстве

5.2. Прямая в пространстве

5.3. Прямая и плоскость в пространстве

6.1. Плоскость

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Математика 1 семестр / Методички / Методичка_4_Ан_геом_в пр.pdf

Скачиваний:

264

Добавлен:

23.02.2015

Размер:

1.17 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

		5.1. Плоскость в пространстве
1.	Ax + By +Cz + D = 0	- общее уравнение плоскости в декартовой системе ко-
	A2 + B2 +C 2 ≠ 0
	ординат ;
2.			- уравнение плоскости, проходящей че-
2.	A(x − x0 ) + B( y − y0 ) +C(z − z0 ) = 0		- уравнение плоскости, проходящей че-
	рез заданную точку (x0 , y0 , z0 ) и перпендикулярной вектору n ={A, B,C} ;

3. ax + by + cz =1 - уравнение плоскости, отсекающей на осях координат ox, oy, oz abc ≠ 0

отрезки a, b и c соответственно;

4. x cos б+ y cos в + z cos г − p = 0 - нормальное уравнение плоскости, где р – расстояние от начала координат до плоскости, а единичный вектор, перпендикулярный плоскости, имеет координаты {cos б, cos в, cos г} ;


5.	Ax + By +Cz + D = 0			- нормальный вид общего уравнения плоскости (знак
5.	±	A2 + B2 +C 2		- нормальный вид общего уравнения плоскости (знак
	нормирующего		множителя		противоположен	знаку D);

6.	d = Ax0	+ By0 +Cz0 + D	-	расстояние от точки (x0 , y0 , z0 )	до плоскости, за-
		A2 + B2 +C 2
	данной общим уравнением;

7.		x − x1	y − y1	z − z1		- уравнение плоскости, проходящей через три

		x2 − x1	y2 − y1	z2 − z1	= 0
		x3 − x1	y3 − y1	z3 − z1
						не лежащие на одной прямой;
	точки (xi , yi , zi ) (i=1,2,3),

8.	cosϕ =	A1 A2 + B1 B2 +C1C2				-	угол	ϕ	между	плоскостями
		+ B2	+C 2	A2	+ B 2
	A2					+C 2
	1	1	1	2	2	2
	Ai x + Bi y +Ci z + Di = 0			( i =1,2) ;

- необходимое и достаточное условие параллельности плоско-

стей Ai x + Bi

y +Ci z = 0

(i =1,2);

10.

- необходимое и достаточное условие перпендикуляр-

A1 A2

+ B1 B2 + C1C2 = 0

ности плоскостей A

i x + Bi y +Ci z = 0 (i =1,2) ;

11.

d =

− D2

- расстояние между двумя параллельными плоскостями

A2 + B2

+C 2

Ax + By + Cz + D1 = 0 и Ax + By + Cz + D2 = 0 .

							5.2. Прямая в пространстве

12.	A1 x + B1 y +C1 z + D1 = 0						- общее уравнение прямой как линии пересечения
	A2 x + B2 y +C2 z + D2 = 0
	двух параллельных						плоскостей;
13.		x − x0	=	y − y0	=	z −z0	- канонические уравнения прямой, проходящей через
13.		l	=	m	=	n	- канонические уравнения прямой, проходящей через
		l		m		n
	точку (x0 , y0 , z0 ) и имеющей направляющий вектор с компонентами {l, m, n} ;
		mx −ly +(ly			− mx )= 0

14.ny −mz +(mz0 −ny0 )= 0 - уравнения прямой в виде проекций на координатные

nx −lz +(lz0 − nx0 )= 00 0

плоскости;

x = x0 +lt

15.y = y0 + mt - параметрические уравнения прямой, проходящей через точку

z = z0 + nt

(x0 , y0 , z0 ) и имеющей направляющий вектор с компонентами {l, m, n} ;

l = B1C2 − B2C1

16.m = C1 A2 −C2 A1 - соотношения между компонентами направляющего векто-

n = A1 B2 − A2 B1

ра прямой и координатами общего уравнения прямой;

17.

x − x1

y − y1

z −z1

- канонические уравнения прямой, проходящей через

− x

− y

− z

точки с координатами (xi , yi , zi ) (i=1,2);

18. cosϕ

l1l2 + m1m2

+ n1n2

угол

между

прямыми

l 2 + m2

+ n2

l 2

+ m2

+ n2

x − x0

y − y0

= z −z0

(i=1,2), проходящими через точку (x0 , y0 , z0 ) ;

19.

условие

параллельности двух прямых

x − x0

y − y0

z −z0

(i=1,2);

20.

условие перпендикулярности

двух

прямых

l1l2

+ m1m2 + n1n2

= 0

x − x0

y − y0

z −z0

(i=1,2);


		5.3. Прямая и плоскость в пространстве
21.					− уравнение пучка		плоскостей,
21.	A1 x + B1 y +C1 z + D1 + λ( A2 x + B2 y +C2 z + D2 ) = 0				− уравнение пучка		плоскостей,
	проходящих	через	прямую,	заданную		общим	уравнением

A1 x + B1 y +C1 z + D1 = 0A2 x + B2 y +C2 z + D2 = 0.

x = x0 +lt1

22.y = y0 +mt1z = z0 +nt1, где

t1 = −Ax + By +Cz + D

x−l x0 = y −my0 = z −nz0

- координаты точки пересечения прямой

и плоскости Ax + By +Cz + D = 0 ;

23. sinϕ =	Al + Bm +Cn	- угол между прямой	x − x0	=	y − y0	= z −z0	и
23. sinϕ =	A2 + B2 +C 2 l 2 + m2 + n2	- угол между прямой	x − x0	=	y − y0	= z −z0	и
	A2 + B2 +C 2 l 2 + m2 + n2		l		m	n
плоскостью Ax + By +Cz + D = 0 ;
		17

24.

- условие перпендикулярности прямой

x − x

y − y

z −z

Al + Bm +Cn = 0

плоскости Ax + By +Cz + D = 0 ;

x − x

y − y

z −z

25.

A B C

- условие параллельности прямой

плос-

= n

кости Ax + By +Cz + D = 0 .

6.РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

ВПРОСТРАНСТВЕ

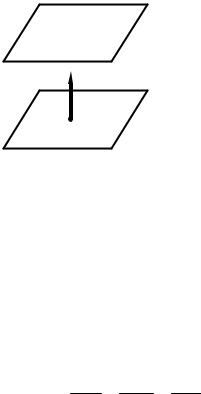
Задача 1. Составьте уравнение плоскости Р, проходящей через точку M 0 : а) параллельно плоскости P1 ;

б) перпендикулярно прямой L;

в) перпендикулярно двум плоскостям P1 и			P2 .
	Решение:	а). Плоскость	проходит через точку
M 0	M 0 (3,−2,−7) параллельно плоскости P1 , заданной урав-

Pнением 2x −3z +5 = 0 . В качестве нормального вектора искомой плоскости Р можно выбрать нормальный вектор плоскости P1 . Плоскость P1 задана общим уравне-

n1	нием	Ax + By +Cz + D = 0 , в котором коэффициенты А,
n1	В, С являются компонентами нормального
	В, С являются компонентами нормального
вектора, значит,	n1 ={2,0,−3} = n	и уравнение плоскости Р может быть записано
в виде уравнения плоскости, проходящей через точку M 0 (x0 , y0 , z0 ) с нормаль-
ным вектором	n ={A, B,C} :

A(x −x0 ) + B( y − y0 ) +C(z −z0 ) = 0, т.е. 2(x −3) −3(z +7) = 0 ,	которое после приведения
к виду общего уравнения плоскости принимает вид:	P : 2x −3z − 27 = 0 .

б). Плоскость проходит через точку M 0 (1,1,1) перпендикулярно

прямой L: x 5−1 = y +2 2 = z−+11 . В качестве нормального вектора искомой плоско-

сти выбираем направляющий вектор прямой L, имеющий компоненты a ={5,2,−1} из канонических уравнений данной прямой L.

n P

		Уравнение плоскости, проходящей через точку M 0 (1,1,1) с
		Уравнение плоскости, проходящей через точку M 0 (1,1,1) с
L		нормальным вектором n ={5,2,−1} , имеет вид:
	M 0	5(x −1) + 2( y −1) −(z −1) = 0 → 5x + 2 y − z −6 = 0 .
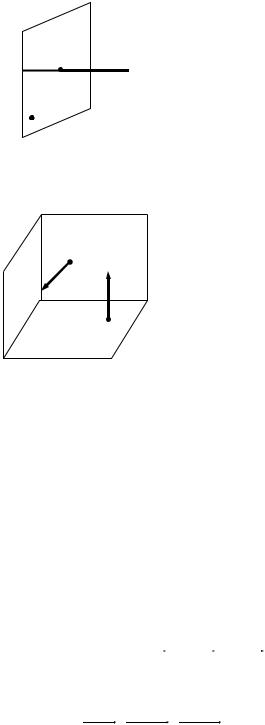
		в). Искомая плоскость проходит через точку M 0 (1,1,−1) и
		перпендикулярна двум плоскостям:
	n1	P1 : 2x − y +5z +3 = 0, n1	={2,−1,5};
	n1	P2 : x +3y − z −7 = 0, n2	={1,3,−1}.
P1		P2 : x +3y − z −7 = 0, n2	={1,3,−1}.
P1		Нормальный вектор искомой плоскости
		Нормальный вектор искомой плоскости
		должен быть перпендикулярен нормальным
n2		векторам плоскостей P1 иP2 . В качестве

Pтакого вектора можно выбрать их векторное произведение:

n = [n1 ×n2 ]=	i	j	k
n = [n1 ×n2 ]=	2	−1 5		= −14i + 7 j + 7k.
	1	3	−1

Уравнение искомой плоскости имеет вид:

−14(x −1) + 7( y −1) + 7(z +1) = 0 2x − y − z − 2 = 0 .

Задача 2. Составьте уравнение плоскости Р , проходящей через три данные точки: M1 (3,−1,2), M 2 (4,−1,−1), M3 (2,0,2).

Решение: Уравнение плоскости получается как следствие компланарности векторов MM1 , M1M 2 , M1M 3 ( M(x,y,z) - текущая координата плоскости), что означает равенство нулю их смешанного произведения:

MM1 M1M 2 M1M 3 =	x −3	y +1	z −2	= 0 3x +3y + z −8 = 0.
	x −3	y +1	z −2
	1	0	−3
	−1	1	0

Задача 3.

а) Найдите отрезки, отсекаемые плоскостью 3x − 4 y − 24z +12 = 0 на коор-

динатных осях.
б) Составьте уравнение плоскости Р, параллельной вектору p ={2,1,−1}	и
отсекающей на координатных осях отрезки a = 3 и b = −2 .	и
в) Напишите уравнение плоскости, проходящей через точку M 0 (1,7,−5)	и
отсекающей от осей координат положительные и равные отрезки.

Решение:

а) Приведем уравнение плоскости к виду уравнения плоскости "в отрезках":

−312x − −412y − −2412z =1 −x4 + −y3 +1/z2 =1,

где a = −4,	b =3,	c = 1	− отрезки,
		2
отсекаемые плоскостью на осях ox, oy, oz соответственно.
б) Уравнение плоскости "в отрезках" принимает вид:				x	+	y	+	z	=1. Приведение
б) Уравнение плоскости "в отрезках" принимает вид:				3	+	−2	+	c	=1. Приведение
				3		−2		c

его к общему виду − 2cx +3cy −6z + 6c = 0 дает плоскость с нормальным вектором n ={−2c,3c,−6}. Из условия параллельности векторов n и p :

(n p) = −4c +3c + 6 = 0 c = 6, n ={2,−3,1} и уравнение плоскости имеет вид:

3x + −y2 + 6z =1 2x −3y + z = 6 .

в) Уравнение плоскости, отсекающей от осей координат положительные и рав-

ные отрезки а, имеет вид:	x + y + z	=1.
	a

Так как плоскость проходит через точкуM 0 (1,7,−5) , a =1 + 7 −5 = 3 и уравнение плоскости принимает вид: x + y + z = 3 x + y + z −3 = 0 .

Задача 4. Найдите угол между плоскостями P1 : x − y − 2z −6 = 0 и P2 : y = 0 . Решение: Один из двух смежных углов (острый) между плоскостями равен уг-

лу между их нормальными векторами n1			={1,−1,− 2}	и	n2 ={0,1,0} и находится
из их скалярного произведения:
cosϕ =	(n1 n2 )	1 0 −1 1 − 2 0		= −	1	ϕ = 60°.
	n1 n2	=			2
		12 +12 +( 2)2 02 +12 +02
Задача 5. Найдите уравнение плоскости, проходящей через точки M (2,−1,4) и
N (3,2,−1) перпендикулярно к плоскости			x + y + z −3 = 0.

Решение: Уравнение плоскости, проходящей через точку М с нормальным вектором n ={A, B,C} , условие прохождения этой плоскости через точку N и условие перпендикулярности этой плоскости и заданной плоскости с нормальным вектором n1 ={1,1,1} дают однородную систему уравнений для определения

А, В, С:

A( x −

2 ) + B( y +1) +C( z −4 ) = 0, A +3B −5C = 0,

A + B +C = 0.

Задача 6. Приведите уравнение плоскости 2x − y + 2z +3 = 0 к нормальному виду и объясните смысл коэффициентов при неизвестных.

Решение: В нормальном уравнении плоскости

x cos б+ y cos в + z cos г − p = 0

коэффициенты представляют собой направляющие косинусы единичного вектора нормали к этой плоскости, которая проходит через начало координат и отстоит от него на расстоянии р. Общее уравнение плоскости Ax + By +Cz + D = 0 с нормальным вектором n ={A, B,C} приводится к нормальному виду путем

умножения на нормирующий множитель м= ±			1	, знак которого про-
умножения на нормирующий множитель м= ±			A2 + B2 +C2	, знак которого про-
тивоположен знаку D. В данной задаче м= −1			и уравнение плоскости
принимает вид:		3
принимает вид:
− 2 x +	1 y −	2 z −1 = 0 2x − y + 2z +3 = 0.
3	3	3
Задача 7. Найдите расстояние от заданной			точки M 0 (−2,−4,3) до плоскости
2x − y + 2z +3 = 0 .

Решение: Расстояние от точки M 0 (x0 , y0 , z0 ) до плоскости с нормальным вектором {A, B,C} равняется

		d = δ = Ax0 + By0 +Cz0 + D .
			±	A2 + B2 +C 2
Здесь	д=	2(−2) −(−4) +2 3 +3	=	−9 = −3 < 0 , то есть начало координат и точка M 0
		− 4 +1+4		3

находятся по одну сторону от плоскости. Искомое расстояние равно d = д =3.

Задача 8. Составьте уравнение плоскости, которая делит пополам двугранный угол, образованный двумя пересекающимися плоскостями: P1 : x −3y + 2z −5 = 0 и

P2 : 3x − 2 y − z +3 = 0.

Решение: Уравнение плоскости найдем из условия равенства отклонений точек этой плоскости M (x, y, z) от двух данных плоскостей:

A1 x + B1 y +C1z + D1			=	A2 x + B2 y +C2 z + D2			, что дает

± A 2	+ B 2	+C 2		± A 2	+ B 2	+C 2
1	1	1		2	2	2

<<< < Предыдущая 1 2 3 45 / 85 6 7 8 > Следующая >>>

Соседние файлы в папке Методички

#
23.02.20152.63 Mб204Методичка 1_Элементарная_математика.pdf
#
23.02.20151.37 Mб89Методичка_2_Матр_Опр_Сист.pdf
#
23.02.20151.69 Mб110Методичка_3_Вект_алг.pdf
#
23.02.20151.17 Mб264Методичка_4_Ан_геом_в пр.pdf
#
23.02.20153.18 Mб112Методичка_5_Ан_геом_на_пл.pdf
#
23.02.20152.73 Mб102Методичка_6_Мат_ан.pdf

Условие существования решения системы ∆ =

= 0 приводит к

уравнению искомой плоскости: 4x −3y − z −7 = 0.