УДК 514.124(075.8) ББК 22.147я 73 А 64

Рецензенты:

кафедра физики Уральского государственного лесотехнического университета; доктор физ. - мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН

Авторы: А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко

А 64 IV. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ В ПРОСТРАНСТВЕ: учебное пособие / А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 41 с.

ISBN 5-321-00633-4

В учебном пособии излагаются теоретические основы аналитической геометрии в пространстве, приводятся решения большого числа задач. Пособие содержит варианты задач (с ответами) для самостоятельного решения, список формул и рекомендуемой литературы.

Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов строительных специальностей направления 6533500 “Строительство” всех форм обучения

Подготовлено кафедрой высшей математики

УДК 514.124(075.8) ББК 22.147я 73

3

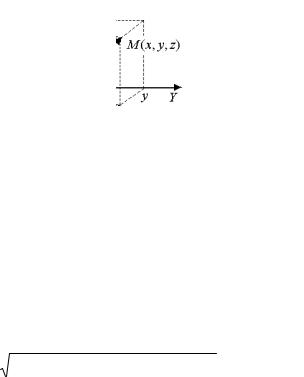
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ В ПРОСТРАНСТВЕ

1.1. Декартовы прямоугольные координаты в пространстве

Положение точки M(x, y, z) в декартовых прямоугольных координатах задается ее проекциями на оси координат.

1.2. Уравнение поверхности

ОПРЕДЕЛЕНИЕ. Уравнением данной поверхности называется такое уравнение с тремя переменными, которому удовлетворяют координаты каждой точки, лежащей на этой поверхности, и не удовлетворяют координаты любой точки, не лежащей на ней: F(x, y, z) = 0.

Поверхность, определенная данным уравнением, есть геометрическое ме-

определяет сферическую поверхность с центром в точке O1 с координатами (x0 , y0 , z0 ) и радиусом R. Действительно, если M (x, y, z) - произвольная точка, то

нию (1) удовлетворяют координаты тех точек, которые равноудалены от O1 на расстояние R, т.е. лежат на сферической поверхности с радиусом R с центром в

точке O1 .

ОПРЕДЕЛЕНИЕ. Поверхность, определяемая в декартовой системе координат алгебраическим уравнением n-й степени, называется алгебраической поверхно-

стью n-го порядка.

1.3. Уравнение линии

В пространственной аналитической геометрии каждая линия рассматривается как пересечение двух поверхностей и определяется заданием двух уравнений.

Если уравнения F1(x, y, z) = 0 и F2(x, y, z) = 0 являются уравнениями двух поверхностей, пересекающихся по линии L, то линия L есть геометрическое место общих точек этих поверхностей, координаты которых удовлетворяют системе уравнений

F (x, y, z) = 0,

L : 1 (2)

F2 (x, y, z) = 0.

4

Пусть f (x, y) = 0 есть уравнение, полученное из системы (2) исключением переменной z. Проекция линии L на плоскость oxy определяется системой урав-

f (x, y) = 0,

нений L :

z = 0.

3. ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

2.1. Плоскость как поверхность первого порядка. Общее уравнение плоскости

Теорема. В декартовых координатах каждая плоскость определяется уравнением первой степени, и каждое уравнение первой степени определяет плоскость.

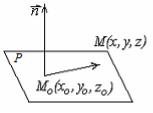
Возьмем на плоскости P произвольную точку M0 (x0 , y0 , z0 ) . Выберем вектор n ={A, B,C}, перпендикулярный плоскости. Пусть M (x, y, z) – произвольная точка, она лежит на

M0 M ={x − x0 , y − y0 , z − z0 }, то их скалярное произведение равно

(n M0M ) = A(x − x0 ) + B( y − y0 ) +C(z − z0 ) .

Уравнение плоскости, проходящей через точку M 0 (x0 , y0 , z0 ) и имеющей нормальный вектор n ={A, B,C}, имеет вид:

A(x − x0 ) + B( y − y0 ) +C(z − z0 ) =0 .

Раскрыв скобки, и обозначив −Ax0 − By0 −Cz0 = D , получим уравнение первой

степени.

Итак, общее уравнение плоскости имеет вид: Ax + By +Cz + D =0.

ПРИМЕР: Составьте уравнение плоскости, проходящей через точку M (1,1,1) перпендикулярно к вектору n ={2,2,3}.

Искомое уравнение примет вид: 2(x −1)+2(y −1)+3(z −1)=0,

2x +2y +3z −7 =0 .

Если два уравнения A1x + B1 y +C1z + D1 =0 и A2 x + B2 y +C2 z + D2 =0 определяют одну и ту же плоскость, то коэффициенты их пропорциональны:

5

2.2. Неполные уравнения плоскостей

Рассмотрим частные случаи уравнения первой степени

Ax + By +Cz + D =0.

1.D = 0: Ax + By + Cz = 0.

Это уравнение определяет плоскость, проходящую через начало координат.

2.A = 0: By + Cz + D = 0. B = 0: Ax + Cz + D = 0.

C = 0: Ax + By + D = 0.

Эти уравнения определяют плоскости, параллельные соответственно координатным осям OX, OY, OZ, так как соответствующие компоненты нормального вектора плоскости равны нулю.

3.A = 0, B = 0: Cz + D = 0. A = 0, C = 0: By + D = 0.

B = 0, C = 0: Ax + D = 0.

Эти уравнения определяют плоскости, параллельные соответственно координатным плоскостям OXY, OXZ, OYZ.

4.A = 0, B = 0, D = 0: Cz = 0. A = 0, C = 0, D = 0: By = 0. B = 0, C = 0, D = 0: Ax = 0.

Эти уравнения определяют координатные плоскости XOY, XOZ,YOZ.

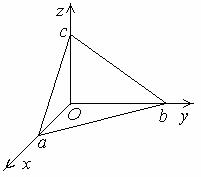
2.3. Уравнения плоскости «в отрезках»

Подвергнем тождественному преобразованию уравнение плоскости в общем виде :

Ax + By +Cz + D = 0

Ax + By +Cz = −D,

координатных осях, называется уравнением плоскости «в отрезках».

ПРИМЕР: Какие отрезки отсекает на осях координат плоскость

2x – 4y + 6z –12 = 0 ?

6

Приведем общее уравнение плоскости к виду уравнения «в отрезках»:

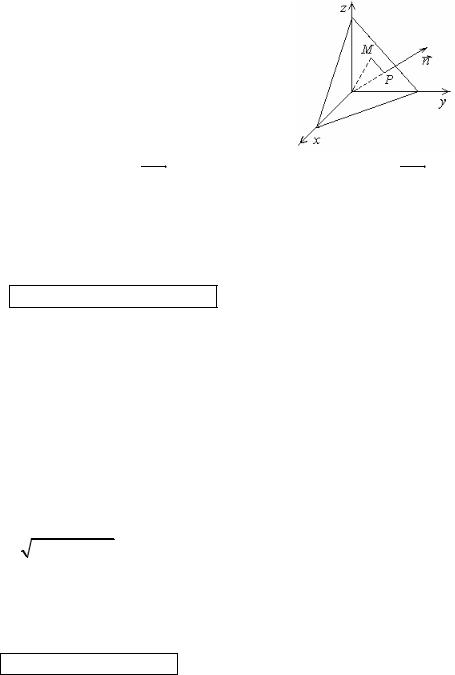
2.4. Нормальное уравнение плоскости

Пусть дана плоскость π. Проведем через начало координат прямую n, перпендикулярную к плоскости π (нормаль), и обозначим через P точку пересечения плоскости и нормали. На нормали введем положительное направление, обозначим углы, которые составляет нормаль с ося-

возьмем произвольную точку M(x, y, z), OM ={x, y, z}. Проекция вектора OM на нормаль n равна прn OM =OM n0 = x cos б+ y cosв+ z cos г .

Если известна длина отрезка OP = p, то уравнение x cos б+ y cos в + z cos г = p задает нормальное уравнение плоскости π в виде

x cos б+ y cos в + z cos г − p = 0 ,

где cos б,cos в, cos г - направляющие косинусы нормали к плоскости, а p – расстояние от плоскости до начала координат.

Приведем общее уравнение плоскости Ax + By + Cz + D = 0 к нормальному виду:

x cos б+ y cos в + z cos г − p = 0 .

Так как эти уравнения определяют одну и ту же плоскость, то их коэффициенты пропорциональны: cos б = мA, cosв = мB, cos г = мC, − p = мD .

Из условия cos2 б+cos2 в+cos2 г =1, которому удовлетворяют направляющие ко-

мD <0 , то есть должен быть противоположен знаку свободного члена нормируемого уравнения. Домножением на нормирующий множитель м общее уравнение плоскости приводится к нормальному виду:

мAX +мBy +мCz +мD = 0.

7