Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка_5_Ан_геом_на_пл

.pdf

Скачиваний:

112

Добавлен:

23.02.2015

Размер:

3.18 Mб

Скачать

☆

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

V. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ.

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Федеральное агентство по образованию РФ

ГОУ ВПО «Уральский государственный технический университет – УПИ» Институт образовательных информационных технологий

V. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ.

ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА

Учебное пособие

Научный редактор – доц., канд. физ. - мат. наук О.А. Кеда

Печатается по решению редакционно-издательского совета УГТУ-УПИ

Екатеринбург

2006

УДК 514.123.2(075.8) ББК 22.147 я 73 А 64

Рецензенты:

кафедра физики Уральского государственного лесотехнического университета; доктор физ. - мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН

Авторы: А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко

А 64 V. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА: Учебное пособие / А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 92 с.

ISBN 5-321-00633-4

В учебном пособии излагаются теоретические основы аналитической геометрии на плоскости и понятий о поверхностях второго порядка, формулы аналитической геометрии на плоскости, приводятся решения большого числа задач. Пособие содержит варианты задач с ответами для самостоятельного решения, задания расчетно-графической работы «Линии на плоскости», список формул и рекомендованной литературы.

Рекомендовано Уральским отделением Учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов строительных специальностей направления 6533500 “Строительство” всех форм обучения

Подготовлено кафедрой высшей математики

УДК 514.123.2(075.8) ББК 22.147 я 73

ISBN 5-321-00633-4	© ГОУ ВПО «Уральский государственный
	технический университет – УПИ», 2006

ОГЛАВЛЕНИЕ
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ...............................................................	5
ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ.........	5
1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ...........................................................................	5
1.1. Расстояние между двумя точками..................................................................................	5
1.2. Деление отрезка в данном отношении...........................................................................	5
1.3. Площадь треугольника....................................................................................................	6
2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ.......................................................................................	6
2.1. Общее уравнение прямой................................................................................................	6
2.2. Каноническое уравнение прямой...................................................................................	6
2.3. Уравнение прямой, проходящей через две точки.........................................................	7
2.4. Уравнение прямой, проходящей через данную точку в заданном направлении.......	7
2.5. Уравнение прямой в отрезках.........................................................................................	7
2.6. Нормальное уравнение прямой ......................................................................................	8
2.7. Расстояние от точки до прямой......................................................................................	8
2.8. Координаты точки пересечения двух прямых..............................................................	8
2.9. Угол между двумя прямыми...........................................................................................	9
2.10. Условие параллельности и перпендикулярности двух прямых................................	9
2.11. Уравнение пучка прямых..............................................................................................	9
3. КРИВЫЕ ВТОРОГО ПОРЯДКА..............................................................................................	10
3.1. Эллипс.............................................................................................................................	10
3.2. Окружность.....................................................................................................................	11
3.3. Гипербола .......................................................................................................................	11
3.4. Парабола.........................................................................................................................	13
4. ПРЕОБРАЗОВАНИЯ КООРДИНАТ .......................................................................................	14
4.1. Параллельный перенос..................................................................................................	14
4.2. Поворот координатных осей.........................................................................................	14
4.3. Изменение начала координат и поворот осей.............................................................	15
4.4. Приведение общего уравнения кривой второго порядка к каноническому виду...	16
5. ЛИНИИ В ПОЛЯРНОЙ СИСТЕМЕ КООРДИНАТ...............................................................	17
5.1. Полярные координаты на плоскости ...........................................................................	17
5.2. Связь полярных координат с декартовыми.................................................................	17
5.3. Уравнение линий в полярной системе координат и их геометрическое изображение
...........................................................................................................................................	18
5.3.1. Кривые второго порядка.....................................................................................................	18
5.3.2. Спирали................................................................................................................................	19
5.3.3. Розы......................................................................................................................................	19
6. ПАРАМЕТРИЧЕСКОЕ ЗАДАНИЕ ЛИНИЙ ..........................................................................	22
6.1. Окружность.....................................................................................................................	22

6.2. Циклоида.........................................................................................................................	22
6.3. Астроида.........................................................................................................................	23
7. КРИВЫЕ ТРЕТЬЕГО ПОРЯДКА.............................................................................................	23
7.1. Полукубическая парабола.............................................................................................	23
7.2. Локон Аньези .................................................................................................................	24
7.3. Декартов лист.................................................................................................................	24
8. КРИВЫЕ ЧЕТВЕРТОГО ПОРЯДКА.......................................................................................	25
8.1. Улитка Паскаля..............................................................................................................	25
8.2. Кардиоида.......................................................................................................................	25
8.3. Лемниската Бернулли....................................................................................................	26
9. ФОРМУЛЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ ..................................	27
10. РЕШЕНИЕ ЗАДАЧ ПО АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ.............	34
12. РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА «ЛИНИИ НА ПЛОСКОСТИ» ..........................	62
13. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА...............................................................................	68
13.1. Поверхности.................................................................................................................	68
13.2. Линейчатые поверхности............................................................................................	68
13.3. Поверхности вращения................................................................................................	68
13.4. Поверхности второго порядка....................................................................................	69
14. ИССЛЕДОВАНИЕ ФОРМЫ ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА ПО ИХ
КАНОНИЧЕСКИМ УРАВНЕНИЯМ......................................................................................	69
14.1. Эллипсоид.....................................................................................................................	70
14.2. Гиперболоиды..............................................................................................................	71
14.2.1. Однополостный гиперболоид..........................................................................................	71
14.2.2. Двуполостный гиперболоид.............................................................................................	72
14.3. Параболоиды................................................................................................................	72
14.3.1. Эллиптический параболоид.............................................................................................	72
14.3.2. Гиперболический параболоид..........................................................................................	73
14.4. Конус.............................................................................................................................	73
14.5. Цилиндры......................................................................................................................	74
14.5.1. Эллиптический цилиндр...................................................................................................	74
14.5.2. Гиперболический цилиндр...............................................................................................	74
2.5.3. Параболический цилиндр...................................................................................................	74
15. РЕШЕНИЕ ТИПИЧНЫХ ЗАДАЧ..........................................................................................	75
16. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ...............................................................	79
ВИД ПОВЕРХНОСТЕЙ ВТОРОГО ПОРЯДКА.........................................................................	85
БИБЛИОГРАФИЧЕСКИЙ СПИСОК ..........................................................................................	91

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ НА ПЛОСКОСТИ

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ

1.ПРОСТЕЙШИЕ ЗАДАЧИ НА ПЛОСКОСТИ

1.1. Расстояние между двумя точками

Пусть даны две точки M1(x1,y1) и M2(x2,y2). Расстояние между ними равно длине вектора

M1M2 ={x2 − x1 ,y2 − y1} и может быть вычислено по формуле

d= M1M2 = (x2 − x1 )2 +(y2 − y1 )2 .

1.2.Деление отрезка в данном отношении

Точка M(x,y) делит отрезок M1M2 в отношении λ, если

M1M

= λ .

MM2

, а отсюда

Тогда

M1M

= λ

x − x1

y − y1

= λ, и координаты точки М находятся по формулам:

x − x

− y

x1 +λ x2

x =

1+λ

y1 +λ y2

y =

1+λ

Координаты середины отрезка С получаются при М1М=ММ2, т.е. λ =1: xc = x1 +2 x2 , yc = y1 +2 y2 .

Отметим, что число λ не зависит от того, как выбрано положительное направление на отрезке М1М2, так как при изменении направления на противоположное λ не меняется.

Число λ может быть положительным или отрицательным числом, может равняться нулю или принимать бесконечное значение в зависимости от расположения точки М на отрезке М1М2:

Но λ не принимает значение -1, так как при λ =-1:

M1M = −MM 2 и M1M + MM 2 = M1M 2 = 0,

т.е. точка М1 совпадает с точкой М2, а мы предполагали их различными.

		1.3. Площадь треугольника
y	M3	Пусть треугольник задан координатами своих вершин:
			М1(x1,y1),
			M2(x2,y2),
		Тогда	M3(x3,y3).
M1	M2	Тогда		x1	y1		1
M1	M2
0		x	1
		S =	1	x	y		1
			2	2		2	1
				x	y		1
				3		3

При вычислении по этой формуле площадь получается положительной, если обход вершин в порядке нумерации происходит против часовой стрелки, и отрицательной – в противоположном случае.

Формула площади треугольника может быть записана в виде

S =	1	x2 − x1		y2	− y1	.

	2	x	− x	y	− y

		3	1	3	1

2. ПРЯМАЯ ЛИНИЯ НА ПЛОСКОСТИ

2.1. Общее уравнение прямой

Общее уравнение прямой на плоскости xoy получается из общего уравнения плоскости в пространстве при z=0.

Прямая на плоскости в декартовых координатах задается уравнением

Ax+By+C=0.

Если А=0 (В=0), то прямая параллельна оси ox (оси oy). Если С=0, то прямая проходит через начало координат.

Если прямая проходит через точку (x0,y0) перпендикулярно вектору n = {A, B}, ее уравнение принимает вид: A(x − x0 ) + B( y − y0 ) = 0 .

2.2. Каноническое уравнение прямой

Если прямая проходит через точку (x0,y0) параллельно направляющему вектору a ={l,m}, то из канонических и параметрических уравнений прямой в

пространстве при z=0 получаем каноническое и параметрические уравнения прямой на плоскости в виде:

x − x	0	=	y − y	0	x = x0 + lt,
					и	+ mt,
l			m
					y = y0

где t - параметр, t (−∞,∞).

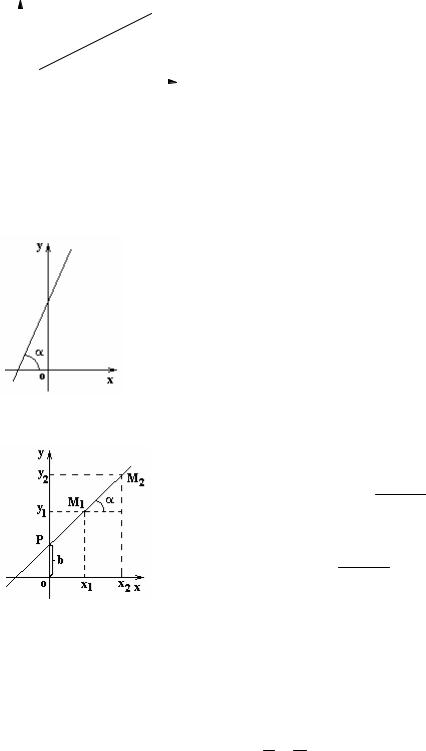
2.3. Уравнение прямой, проходящей через две точки

Пусть на

плоскости заданы

две

точки M1(x1,y1),

M2(x2,y2). Для того чтобы написать уравнение прямой,

проходящей

через

эти точки,

полагаем

соответствующем уравнении прямой в пространстве

X z = z1 = z2 =0.

Тогда

получаем

искомое уравнение

виде

x − x1

y − y1

x − x

− y

2.4. Уравнение прямой, проходящей через данную точку в заданном направлении

Пусть прямая составляет угол α с осью ох. Угловым коэффициентом прямой k называется число k =tgα.

Прямая может быть задана точкой М1(x1,y1) и угловым коэффициентом k или двумя точками М1(x1,y1) и М2(x2,y2).

Уравнение прямой с угловым коэффициентом k может быть получено из общего уравнения прямой Ax+By+C=0,

если B ≠ 0, тогда	y = k x +b, где k = −	А	и b = −	C	.
		B		B

Пусть прямая пересекает ось oy в точке P(0,b).

Из уравнения прямой, проходящей через две точки, имеем

y − y1 = y2 − y1 (x − x1) . x2 − x1

,Отсюда

y2 − y1 = tgα = k . x2 − x1

Таким образом y − y1 = k(x − x1).

Уравнение полученной прямой принимает вид уравнения прямой с угловым коэффициентом k, если b=y1 - k x1.

2.5. Уравнение прямой в отрезках

Общее уравнение прямой Ax+By+C=0 может быть преобразовано к виду уравнения прямой “в отрезках”: ax + by =1.

Прямая в отрезках пересекает ось ox в точке А(а,0) и ось oy в точке В(0,b).

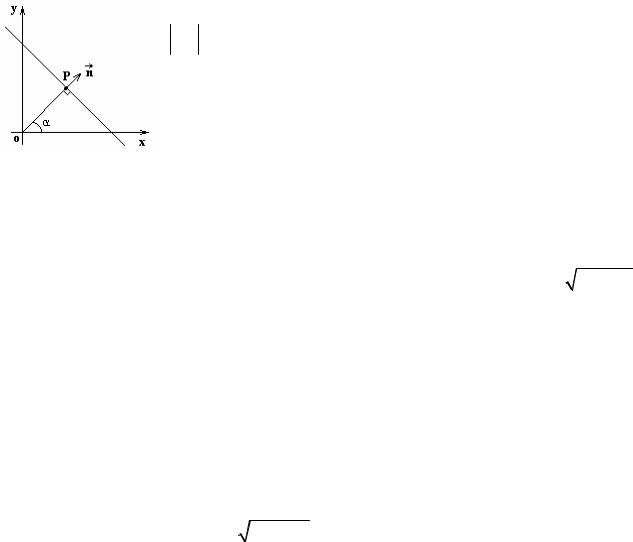
2.6. Нормальное уравнение прямой

Пусть известно расстояние от прямой до начала координат OP = p и угол α между перпендикуляром к прямой и

осью ox. Из нормального уравнения плоскости в пространстве, полагая z=0 и учитывая, что

π
cos	−α = sin α,
2
получаем нормальное уравнение прямой на плоскости в
виде
xcosα+ ysin α− p =0.
Нормальное уравнение прямой можно получить из общего уравнения
прямой Ax+By+C=0, умножив его на нормирующий множитель µ = ±		1	.
		A2 + B2	.

Знак числа µ должен быть противоположен знаку числа С.

Косинусы углов, образуемых прямой с осями координат, называются

направляющими косинусами прямой.

Если угол между прямой и осью ox равен α и угол между прямой и осью oy равен β, то cos2 α +cos2 β =1.

2.7. Расстояние от точки до прямой

Расстояние d от точки M0(x0,y0) до прямой, задаваемой нормальным уравнением, равно модулю отклонения точки от прямой δ , d=|δ |, где

δ= x0 cosα+ y0 sin α− p = ± Ax0 +2By0 +2 C .

A + B

По этой формуле δ положительно, если точка М0 и начало координат лежат по разные стороны от прямой, в противном случае δ отрицательно.

2.8. Координаты точки пересечения двух прямых

Если прямые заданы уравнениями A1x+B1y+C1=0 и A2x+B2y+C2=0, то координаты точки их пересечения (x0, y0) получаются как решение системы уравнений

A x + B y +C = 0,

A2 x + B2 y +C2 = 0

по формулам Крамера в виде x =

, y =

, при

≠ 0.

А2


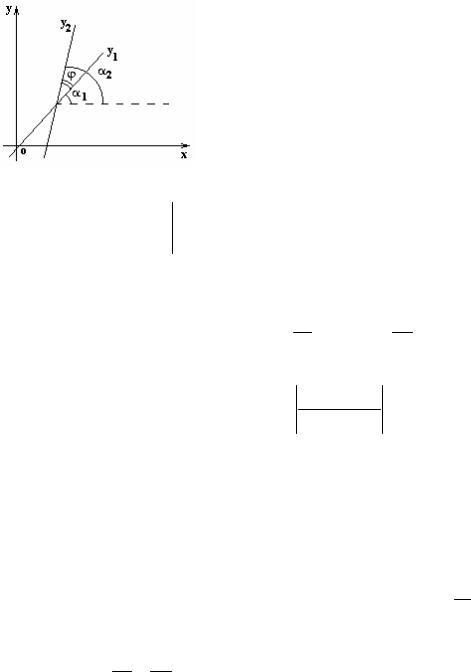
Отсюда tgϕ =		k2 −k1
Отсюда tgϕ =	1+ k k
	1+ k k
	2		1

2.9. Угол между двумя прямыми

Пусть две прямые заданы уравнениями: y1 = k1x +b1,

y2 = k2 x +b2.

Острый угол ϕ пересечения этих прямых (отсчитываемый против часовой стрелки) находится из следующих соотношений:

tgϕ = tg(α2 − α1) =		tgα2 −tgα1	.
tgϕ = tg(α2 − α1) =	1 + tgα1tgα2		.
	1 + tgα1tgα2

Если прямые заданы общими уравнениями А1x+B1y+C1=0 и A2x+B2y+C2=0, то угловые коэффициенты прямых равны

tgα1 = − A1 , tga2 = − A2 B1 B2

и угол ϕ между прямыми определяется формулой

tgϕ= A1B2 − A2 B1 . A1 A2 + B1B2

2.10. Условие параллельности и перпендикулярности двух прямых

Прямые y1=k1x+b1 и y2=k2x+b2 параллельны друг другу, если ϕ = 0 . Следовательно, tgϕ= 0, то есть k1=k2.

Прямые y1=k1x+b1 и y2=k2x+b2 перпендикулярны друг другу, если ϕ= π2 .

Следовательно, tgϕ →∞, то есть k1k2 = -1. Отсюда k1 = − 1 . k2

Если прямые заданы общими уравнениями:

А1В1-А2В1=0, A1 = A2 - условие параллельности,

B1 B2

А1А2+В1В2=0 - условие перпендикулярности прямых.

2.11. Уравнение пучка прямых

Совокупность всех прямых плоскости, проходящих через некоторую точку M(x0,y0), называется пучком прямых с центром М.

Пусть A1x+B1y+C1=0 и A2x+B2y+C2=0 - уравнения двух прямых, пересекающихся в точке М; α и β - произвольные числа, одновременно не равные нулю, тогда

α(A1x+B1y+C1)+β(A2x+B2y+C2)=0 - уравнение прямой, проходящей через точку М.

1 / 101 2 3 4 5 6 7 8 9 10 > Следующая >>>

Соседние файлы в папке Методички

#
23.02.20152.63 Mб204Методичка 1_Элементарная_математика.pdf
#
23.02.20151.37 Mб89Методичка_2_Матр_Опр_Сист.pdf
#
23.02.20151.69 Mб110Методичка_3_Вект_алг.pdf
#
23.02.20151.17 Mб264Методичка_4_Ан_геом_в пр.pdf
#
23.02.20153.18 Mб112Методичка_5_Ан_геом_на_пл.pdf
#
23.02.20152.73 Mб102Методичка_6_Мат_ан.pdf