
Математика 1 семестр / Методички / Методичка_3_Вект_алг
.pdfIII. ВЕКТОРНАЯ АЛГЕБРА
Федеральное агентство по образованию ГОУ ВПО «Уральский государственный технический университет – УПИ»
Институт образовательных информационных технологий
III. ВЕКТОРНАЯ АЛГЕБРА
Учебное пособие
Научный редактор – доц., канд. физ. - мат. наук О.А. Кеда
Печатается по решению редакционно-издательского совета УГТУ-УПИ
Екатеринбург
2006
УДК 514.742.2(075.8) ББК 22.151.5я 73 В 26
Рецензенты:
кафедра физики Уральского государственного лесотехнического университета; доктор физ. - мат. наук, проф. А.П. Танкеев, зав. лабораторией ИФМ УрО РАН
Авторы: А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко
В 26 III. ВЕКТОРНАЯ АЛГЕБРА: учебное пособие /
А.Б. Соболев, М.А. Вигура, А.Ф. Рыбалко, Н.М. Рыбалко. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 56 с.
ISBN 5-321-00633-4
Учебное пособие предназначено для обеспечения самостоятельной работы студентов содержит краткое изложение теории, примеры решения задач и пять вариантов заданий для самостоятельной работы, состоящие из 17 задач с ответами, а также тесты для быстрого контроля знаний. Каждый студент выполняет один из вариантов заданий и оформляет отчетную работу, состоящую из условия, решения и ответа к каждой из задач своего варианта.
Рекомендовано Уральским отделением учебно-методического объединения вузов РФ в области строительного образования в качестве учебного пособия для студентов специальностей направления 6533500 «Строительство» всех форм обучения
Подготовлено кафедрой высшей математики
УДК 514.742.2(075.8) ББК 22.151.5я 73
ISBN 5-321-00633-4 |
© ГОУ ВПО «Уральский государственный |
|
технический университет – УПИ», 2006 |
ОГЛАВЛЕНИЕ |
|
1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ................................ |
4 |
1.1. Определение вектора..................................................................................... |
4 |
1.2. Линейные операции над векторами и их свойства..................................... |
4 |
1.3. Базис и координаты........................................................................................ |
9 |
1.3.1. Декартов прямоугольный базис и декартова система координат...... |
9 |
1.3.2. Проекция вектора на ось ........................................................................ |
10 |
1.3.3. Декартова прямоугольная система координат..................................... |
11 |
1.4. Скалярное произведение векторов............................................................... |
12 |
1.4.1. Алгебраические свойства скалярного произведения векторов.......... |
12 |
1.4.2. Выражение скалярного произведения векторов в декартовых |
|
координатах............................................................................................. |
13 |
1.4.3. Геометрические приложения скалярного произведения векторов ... |
13 |
1.5. Векторное произведение векторов............................................................... |
14 |
1.5.1. Алгебраические свойства векторного произведения векторов.......... |
15 |
1.5.2. Выражение векторного произведения векторов в декартовых |
|
координатах............................................................................................. |
16 |
1.5.3. Геометрические свойства векторного произведения векторов.......... |
17 |
1.6. Смешанное произведение векторов............................................................. |
17 |
1.6.1. Выражение смешанного произведения в декартовых координатах.. |
18 |
1.7. Преобразование координат вектора при преобразовании базиса............. |
20 |
2. ЗАДАЧИ С РЕШЕНИЯМИ.................................................................................. |
22 |
2.1. Векторы, базисы, координаты....................................................................... |
22 |
2.2. Переход к новому базису, преобразование координат .............................. |
24 |
2.3. Построение ортогонального базиса.............................................................. |
25 |
2.4. Декартов прямоугольный базис. Направляющие косинусы и |
|
координаты ...................................................................................................... |
26 |
2.5. Скалярное произведение векторов............................................................... |
27 |
2.6. Векторное произведение векторов............................................................... |
30 |
2.7. Смешанное произведение векторов............................................................. |
32 |
2.8. Разные задачи ................................................................................................. |
35 |
3. ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ......................................... |
38 |
3.1. Ответы к задачам для самостоятельной работы......................................... |
44 |
4. ПРОВЕРОЧНЫЙ ТЕСТ: ВЕКТОРНАЯ АЛГЕБРА........................................... |
47 |
5. Приложение 1. Система аксиом геометрии Г. Вейля........................................ |
51 |
6. Приложение 2. Основные формулы и обозначения .......................................... |
52 |
7. БИБЛИОГРАФИЧЕСКИЙ СПИСОК.................................................................. |
55 |

1.ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ВЕКТОРНОЙ АЛГЕБРЫ
1.1.Определение вектора
ОПРЕДЕЛЕНИЕ. Вектором называетсяJJGнаправленный отрезок прямой.
Вектор обозначается либо значком AB , где точки A и B задаютG начало и конец вектора, либо одной строчной буквой a .
На чертеже будем обозначать вектор стрелкой. Начало вектора называется точкой его приложения.
Для обозначения длины вектора будем пользоваться символом модуля или aG .
JJG
AB
ОПРЕДЕЛЕНИЕ. Вектор называется нулевым, если начало и конец его совпадают.
Нулевой вектор не имеет определенного направления и имеет длину, равную нулю.
ОПРЕДЕЛЕНИЕ. Векторы называются коллинеар-
ными, если они лежат либо на одной прямой, либо на параллельных прямых.
ОПРЕДЕЛЕНИЕ. Два вектора называются равными, если они коллинеарны, имеют одинаковую длину и направление. Все нулевые векторы считаются равными.
G JJJG
Для каждого вектораG JJJGa =OA существует противопо-
ложный вектор −a =OA' , коллинеарный вектору a , имеющий ту же длину и противоположное направление.
Точка приложения вектора может быть выбрана произвольно. Так, на рисунке справа изображен один и тот же вектор.
ОПРЕДЕЛЕНИЕ. Вектор называется параллельным некото-
рой плоскости, если он лежит на прямой, параллельной этой плоскости.
ОПРЕДЕЛЕНИЕ. Векторы, параллельные одной и той же плоскости, называются компланарными.
1.2.Линейные операции над векторами и их свойства
Линейными операциями над векторами называются сложение векторов и умножение вектора на вещественное число.
4
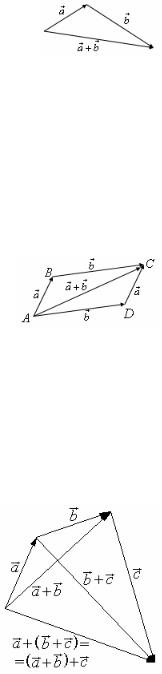
ОПРЕДЕЛЕНИЕ. |
Суммой aG +b двух векторов a и b называется вектор, |
||||||
идущий из начала вектора aG в конец вектора b при условии, что вектор b при- |
|||||||
ложен к концу вектора aG. |
|||||||
|
Правило сложения векторов, изложенное в этом определе- |
||||||
нии, обычно называют правилом треугольника. |
|||||||
|
Правило сложения векторов обладает следующими свойст- |
||||||
вами: |
G |
G |
|
G |
|
|
|
1) |
G |
|
|
|
|||
a +b |
=b |
+ a (переместительное свойство); |
|||||
2) |
G |
G |
G |
G |
G |
G |
|
(a |
+b )+c |
= a + |
(b |
+c ) (сочетательное свойство); |
|||
3) существует нулевой вектор 0 , такой, что |
aG +0 = aG |
для любого вектора a |
|||||||||
(особая роль нулевогоGвектора); |
|
|
G′ |
||||||||
4) для каждого вектора a |
существует противоположный ему вектор a , такой, |
||||||||||
|
G |
G |
G |
|
|
|
|
|
|
|
|
что a |
+ a′ = 0 . |
|
|
|
|
|
|
|
|
||
Доказательство свойства 1). |
|
|
|
|
|||||||
Рассмотрим произвольный параллелограмм |
ABCD . |
JJJG |
|||||||||
|
|
G |
JJJG |
G |
JJJG |
|
|
G |
JJG |
JJG |
|
Пусть a |
= AB , |
b = BC |
. Тогда a |
+b = AC . Но BC = |
AD , |
||||||
JJJG |
JJJG |
JJJG |
JJJG |
JJJG |
G |
G |
|
|
|
||
DC |
= AB |
AC = AD + DC |
=b |
+ a . |
|
|
|
||||
|
|
|
|
G |
G |
G |
G |
|
|
|
|
Таким образом, a +b =b |
+ a . |
|
|
|
|||||||
Замечание. При доказательстве свойства 1) обосновано еще одно правило сло-
жения векторов, |
называемое правилом параллелограмма: если векторы a и |
|||||||
bG |
приложены к общему началу и на них построен параллелограмм, то сумма |
|||||||
G |
G |
этих векторов представляет собой диагональ параллелограмма, идущую |
||||||
a |
+b |
|||||||
из общего начала векторов aG |
и b . |
|||||||
Доказательство свойства 2). |
||||||||
|
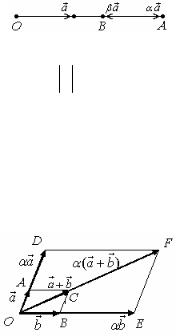
Выполним следующее построение (см. рис.): отложим |
|||||||
вектор bG b |
от конца вектора aG, вектор c от конца векто- |
|||||||
|
G |
|
|
|
G |
G |
идет из начала вектора a в ко- |
|
ра b . Тогда вектор a |
+b |
|||||||
|
|
|
|
G |
|
G |
G |
идет из начала вектора b в |
нец вектора b , вектор b + c |
||||||||
конец вектора cG |
, а векторы |
(aG +b )+cG и aG +(b +cG) оба |
||||||
|
|
|
|
|
|
G |
в конец вектора c , т.е. совпа- |
|
идут из начала вектора a |
||||||||
дают. |
|
|
|
|
|
|
||
Доказательство свойства 3). |
||||||||
|
Пусть |
G |
JJJG |
JJJG |
так как его начало и конец совпадают. Тогда |
|||
G |
a |
= AB , 0 |
= BB , |
|||||
G |
JJJG |
|
JJJG |
JJJG |
G |
|
|
|
a |
+ 0 |
= AB |
+ BB = AB = a , что и требовалось доказать. |
|||||
Доказательство свойства 4).
Для любого вектораG aG существует такой вектор a′= −aG, для которого aG + aG′ = aG + ( − aG) = 0 , что и требовалось доказать.
5

ОПРЕДЕЛЕНИЕ. Произведением αa вектора a на вещественное число α
называется вектор b , коллинеарный вектору a , имеющий длину α a и
имеющий направление, совпадающее с направлением вектора aG в случае α > 0 и противоположное направлению вектора a в случае α < 0 .
Геометрический смысл операции умножения вектора на число:
при умножении вектора aG на число α вектор a "растягивается в α раз".
GG умножения вектора на число обладает следующими свойствами:
5)1 a = a (унитарность);
6)α (βaG)= (αβ )aG (сочетательное свойство числовых сомножителей);
7)(α+β )aG =αaG+ βaG (распределительное свойство умножения вектора на число относительноG суммыG чисел);
8)α(aG+b )=αaG+αb (распределительное свойство умножения вектора на чис-
ло относительно суммы векторов);
Доказательство свойства 5).
Докажем, что 1 a = aG. Для этого докажем, что векторы c =1 aG и dJG = aG рав-
ны: |
|
G |
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
G |
|
|
|
|
|
|
|
|
|
|||||||||||||
вектор c = |
1 a коллинеарен вектору d |
= a по определению произведения векто- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ра на число; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
JG |
|
|
|
|
G |
|
|
|
|
|
|
|
G |
|
|
|
|
G |
|
|
|
|
|
|
JG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|||||||||||
|
d |
= |
|
1 a |
= |
|
1 |
|
|
a |
= |
|
a |
= |
|
|
|
d |
|
, то есть векторы c и d имеют одинаковую длину; |
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
G |
|
|
|
|
JG |
|
|
|
|
G |
|
имеют одинаковое направление, такJGкакG |
G |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
векторы c |
= |
1 a и d |
= a |
|
вектор c =1 a |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
имеет направление, |
совпадающее с направлением вектора d = a |
по определе- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
нию произведения вектора на положительное число. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказательство свойства 6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Докажем что α (βaG)= (αβ )aG. Обозначим c =α(βaG), dG = (αβ )aG . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
Так как α и β - числа, |
|
cG коллинеарен dG |
по определению произведения векто- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
ра на число. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
G |
|
( |
β G |
|
= |
|
α |
|
|
|
β G |
|
= |
|
α |
|
|
|
β |
|
|
|
G |
|
= |
|
αβ |
|
|
|
G |
|
|
G |
|
= |
|
JG |
|
. |
|
||||||||||||||||
|
= |
α |
|
|
|
|
|
|
= |
αβ |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
c |
|
|
|
a) |
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
|
|
|
|
|
|
|
a |
|
( |
|
)a |
|
|
|
d |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рисунке приведен пример взаимного расположения |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
векторов cG и dJG. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Запишем варианты взаимного направления векторов c и d . |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если β > 0, |
βaG |
|
|
направлен так же, как и a . Тогда если α > 0, вектор cG =α(βaG) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
направлен также, как и aG, а если α < 0, вектор c =α(βaG) направлен противо- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
положно вектору aG. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
Если |
β < 0, |
βaG |
|
|
направлен противоположно вектору a . Тогда если α > 0, век- |
|||||||||||||||||||||||||||||||||||||||||||||||||||||
тор cG |
=α( |
βaG) |
направлен противоположно a , а если α < 0, вектор cG =α(βaG) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
6
направлен так же, как и вектор a .
Легко заметить, что такое же направление имеет во всех рассмотренных случа- |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
ях и вектор dJG |
|
= (αβ )aG . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
В случае α = 0 , β = 0 , или aG = 0 |
|
равенство, очевидно, выполняется. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Доказательство свойства 7). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
Докажем, что (α+β )aG =αaG+ βaG. Обозначим c = (α+β )aG и dJG =αaG + βaG . |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
G |
|
JG |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
Векторы c и d коллинеарны вектору a по определению произведения вектора |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
на число, и, следовательно, коллинеарны между собой. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Докажем, что |
G |
|
= |
|
|
JG |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
c |
|
|
|
d |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
Пусть для определенности α > 0, β < 0, |
|
α |
|
> |
|
|
|
β |
|
|
|
|
|
. (См. рис.). |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
G |
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
G |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
c |
= |
|
(α+β )a |
= |
α+β |
|
|
a |
= |
|
|
|
α |
− |
β |
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
dJG |
|
= |
|
OB |
|
= |
|
OA |
|
− |
|
AB |
|
= |
|
αaG |
|
− |
|
βaG |
|
= |
|
α |
|
aG |
|
− |
|
β |
|
|
|
aG |
|
= ( |
|
α |
|
|
− |
|
β |
|
) |
|
aG |
|
= |
|
|
|
α |
|
− |
|
β |
|
|
|
|
aG |
. |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
векторов c и dG |
|||||||||||||||||||||||||||||
|
Так как по |
|
предположению |
|
|
|
α > 0, |
β |
|
< 0, |
|
|
α |
|
|
|
> |
|
β |
|
, направления |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
совпадают.
Остальные случаи соотношения величин и знаков чисел α и β рассматриваются аналогично. G
Очевидно, что равенство выполняется, если α = 0 , β = 0 , или a = 0 .
Доказательство свойства 8). |
|
|
|
|
|||||||
|
|
|
G |
|
G |
|
G |
|
G |
|
|
Докажем, что α(a +b )=αa |
+αb . |
|
|
||||||||
G |
=α |
G |
G |
) |
|
JG |
|
G |
G |
|
|
Обозначим c |
a +b |
и d |
=αa +αb . |
|
|
||||||
G |
JG( |
|
G |
|
|
|
|
|
|
|
|
Если α = 0 , c = d = |
0 - утверждение верно. |
|
|
||||||||
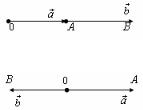
Пусть α > 0, . Рассмотрим случай, когда векторы a и b неколлинеарны. |
|||||||||||
Отложим от точки O векторы |
a и b и сложим их по правилу параллело- |
||||||||||
|
|
|
|
|
|
|
G |
G |
|
|
G G JJJG |
грамма. Полученный вектор a +b умножим на число α . Пусть α (a +b)=OF . |
|||||||||||
Обозначим точками A и B |
концы векторов a и b |
|
соответственно, а точкой |
||||||||
C - конец вектора |
|
|
G |
|
|
|
JJG |
, отложенного от точки O , |
|||
a +b |
. Через конец вектора OF |
|
|||||||||
проведем прямые, параллельные векторам a и b , |
и обозначим точки их пере- |
||||||||||
сечения с продолжениями векторов a и b через D и E соответственно. Тогда
|
OF |
|
|
= |
|
|
OD |
|
|
|
= |
|
OE |
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
OC |
|
|
|
|
OA |
|
|
|
|
OB |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
||||
в силу подобия треугольников |
ODF |
и OAC |
и |
OEF и OBC . Следовательно, |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
JJJG JJJG |
JJJG |
|
|
|
|
|
OD |
|
=α |
|
OA |
|
, |
|
OE |
=α |
OB |
, OD +OE |
= OF |
по правилу параллелограмма. Но тогда |
||
|
|
JJJG |
|
|
|
G |
|
|
G |
|
|
|
|
JJG |
G |
G |
|
|
|
|
|
|
|
|
|
|
|||||||||
OF |
|
=α (a +b) с одной стороны, и OF |
=αa +αb |
– с другой стороны, что и тре- |
|||||||||||||
бовалось доказать. Случай α < 0 рассматривается аналогично.
7
В случае α = 0 , aG = 0 или bG = 0, равенство, очевидно, выполняется.
Рассмотрим случай, когда векторы a и b коллинеарны. Докажем вначале следующееG утверждение:
Утверждение. Если a G– произвольный вектор какой-либо прямой, то любой вектор на этой прямой b может быть записан в виде b =αaG.
Доказательство. Приложим векторы a и b к общему началу O . Тогда эти векторы расположатся на одной прямой, на которой мы выберем начало отсчета,
масштабный отрезок и положительное направление. Воз- |
|
|
||||||||
можны 3 случая: |
|
|
|
|
|
|
||||
G |
G |
|
|
|
|
|
|
|
|
|
1) bG |
= 0G α = 0 , |
|
|
|
|
|
|
|||
2) a |
и b направлены в одну сторону, |
|
|
|
|
|||||
G |
G |
|
|
|
|
|
|
|
|
|
3) a |
и b направлены в разные стороны. |
JJGJ |
|
JJJG |
JJJG |
|||||
|
|
JJJG |
G |
JJJG |
G |
JJG |
если α > 0 |
|||
Пусть OA = a |
≠ 0 , OB =b |
. Тогда |OB |=α |OA|, |
, |OB |= −α |OA|, |
|||||||
если α < 0 . |
|
G |
|
G |
|
|
|
|
||
|
|
|
|
= |
|
|
|
|
||
Во всех трех случаях b |
αa . Действительно, выполняются три условия: |
|||||||||
1) | bG |
|=|α | | aG |
|; |
|
|
|
|
|
|
||
2) bG |
и αaG |
коллинеарны, так как b и a коллинеарны; |
|
|
||||||
3) bG |
и αaG |
при любом значении α (> 0,= 0,< 0) |
направлены в одну сторону. |
|||||||
Используем теперь доказанное утверждение для продолжения доказательства |
|||
свойства 8). |
|
|
|
Обозначим cG =α(aG +bG), dJG =αaG +αbG. |
|||
Тогда cG =α (aG +bG)=α (aG +γ aG)=по свойству 7) = α ((1+γ )a)= α (1 +γ )aG . |
|||
Но dJG =αaG +αbG =αaG +α (γ aG)= по свойству 6) = αa +(αγ )aG = по свойству 7) = |
|||
G |
G |
G |
JG |
= (α+αγ )a =α |
(1 +γ )a , т.е. |
c |
= d , что и требовалось доказать. |
Свойства 1) –8) для векторов, определенных так, как это было сделано выше, в линейной алгебре служат аксиомами так называемого линейного, или векторного, пространства. Таким образом, геометрический вектор (направленный отрезок) является вектором линейного пространства. Векторами линейных пространств также являются вещественные точки пространств R1 ,R2 ,R3 ,...,Rn , числа, матрицы-столбцы, матрицы-строки и другие объекты.
То, что аксиомы линейного пространства выполняются как для вещественных чисел, так и для геометрических векторов, позволяет производить выкладки в векторной алгебре по тем же правилам, по которым производятся аналогичные выкладки в алгебре вещественных чисел.
8
1.3.Базис и координаты
1.3.1.Декартов прямоугольный базис и декартова система координат
ОПРЕДЕЛЕНИЕ. Базисом в пространстве будем называть три некомпланар-
ных вектора, взятые в определенном порядке.
ОПРЕДЕЛЕНИЕ. Базисом на плоскости будем называть два неколлинеарных вектора на этой плоскости, взятые в определенном порядке.
ОПРЕДЕЛЕНИЕ. Базисом на прямой будем называть любой ненулевой вектор этой прямой.
Теорема. Каждый вектор, параллельный какой-либо прямой, может быть разложен по базису наG этой прямой.
То есть еслиGa – произвольный вектор какой-либо прямой, то любой вектор на этой прямой b может быть записан в виде b =αaG.
Следствие. Если два вектора aG = (ax , ay , az ) и b = (bx ,by ,bz ) коллинеарны, то их
координаты пропорциональны, т.е.
ax = ay = az . bx by bz
Теорема. Каждый вектор, параллельный какой-либо плоскости, может быть разложенG по базису на этой плоскости.
То есть если aG и b – произвольные неколлинеарные векторы на плоскости, то любой вектор на этой плоскости с мо-
жет быть записан в виде сG =αaG+ βb .
Доказательство: G
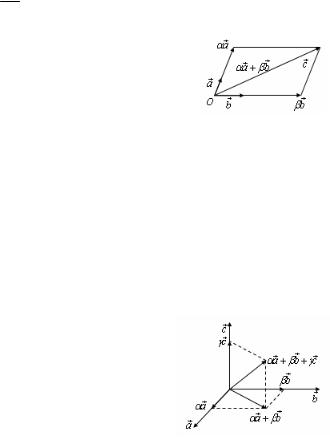
Отложим вектор c от произвольной точки O плоскости. Пусть на этой плоскости задан базис из векторов a и b . Отложим их также от точки O . По-
строим прямые, параллельные векторам a и b , через конец вектора cG. РассмотримG полученный при этом параллелограмм. Его стороны равны αa
и βb , а диагональ, совпадающая с вектором c , равна по правилу параллелограмма cG =αaG+ βbG.
Теорема. Каждый вектор пространства может быть разложен по базису в пространстве.
То есть если aG, b , сG – три некомпланарных вектора в
пространствеG , тоG любой вектор d может быть записан в виде d =αaG+ βb +γcG.
Доказательство. Геометрически вектор d представляет собойGпространственную диагональ параллелепипеда, построенного на векторах aG, b и с. Замечание. Числа α, β, γ называются координатами вектора в соответствующем базисе.
9
