2.7. Расчеты потокораспределения в кольцевой и разомкнутой цепи.

РАСЧЕТ СЕТИ С ДВУСТОРОННИМ ПИТАНИЕМ

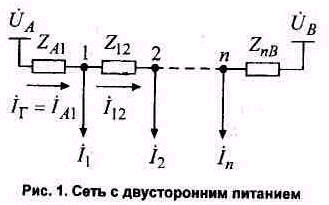
Алгоритм расчета сети с двусторон­ним питанием зависит от уровней напря­жений по концам передачи U_А и U_В (рис. 1), при этом возможны случаи ра­венства напряжений U_А = U_В и их нера­венства U_А ≠ U_В . Попутно заметим, что расчет кольцевой сети является частным случаем расчета сети с двусторонним пи­танием при равенстве напряжений по концам передачи.

Правило моментов для токов и мощностей

Рассмотрим сеть с двусторонним питанием, показанную на рис. 1. Нагруз­ки узлов 1, 2,..., п заданы в токах , I₁,...,I_n„ напряжения узлов А и В одина­ковы (U_А = U_В). Зададим произвольно направления токов в сети на всех ее участках и обозначим их I_A1 I₁₂ I_nB.

Учитывая равенство напряжений по концам передачи, определим

(1)

(2)

(3)

Выразим токи участков сети через ток на головном участке сети I_Г=I_A1 и токи нагрузок на основе I закона Киргофа:

(4)

Теперь подставим токи (1.2) в (1.1) и выразим головной ток:

Выражение для I_Г получило название правила моментов для токов. Действительно, для определения тока на головном участке I_Г вычисляются моменты токов по отношению к противоположному узлу В. Здесь токи нагрузок высту­пают в роли силы, а сопротивления ветвей от точки подключения нагрузки до узла В — в роли плеча.

Правило моментов можно записать и для мощностей при введении неко­торых ограничений:

- напряжения узлов 1,2,..., п одинаковы и равны U_А,

Т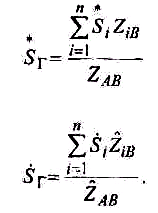еперь, если умножить правую и левую части соотношения для I_Г на U_А√3 и учесть равенство напряжений узлов, можно получить

Метод преобразования сети

Для расчетов вручную параметров установившихся режимов сложнозамкнутых электрических сетей может быть использован метод преобразования се­ти. Суть этого метода сводится к приведению сети к более простому виду (одному кольцу или разомкнутой сети). Упрощенная сеть рассчитывается с ис­пользованием известных методов и затем производится обратное преоб­разование сети к исходному виду. При использовании метода преобразования применяются приемы разноса нагрузок по концам участка сети и из центра звезды, объединения, концевых источников питания и нагрузок, преобразова­ния пассивных частей схем электрической сети. Метод преобразования должен применяться с соблюдением условия неизменности параметров установивше­гося режима сети, внешней по отношению к преобразуемой ее части. Кроме то­го, при использовании приемов преобразования необходимо оговаривать пред­варительно все принимаемые допущения.

Разнос нагрузок по концам участка

Метод контурных уравнений

Метод контурных уравнений предназначен для расчета параметров уста­новившихся режимов сложнозамкнутых электрических сетей. Суть метода за­ключается в составлении и решении системы контурных уравнений и опреде­лении на их основе параметров режима. Система контурных уравнений может быть записана в форме токов или мощностей. Число независимых контурных уравнений соответствует числу независимых контуров схемы. Составление контурных уравнений опирается на использование I и II законов Кирхгофа.

Рассмотрим вывод контурных уравнений для сети, показанной на рис. Число независимых контуров схемы k определяется в зависимости от числа уз­лов схемы без балансирующего (п -1) = 3 и числа линий т= 5:

k=m-(n-1)=2.

Зададим условные направления токов в ветвях сети и обхода контуров, причем направления обходов контуров I и II зада­дим совпадающими соответственно с ус­ловными направлениями токов в ветвях

б—1 и 1—2 (I_б1 и I₁₂). Токи I_б1 и I₁₂ назовем контурными токами I₁ и I₁₁

Запишем I закон Кирхгофа с учетом условного направления токов для всех узлов схемы, кроме балансирующего, выразив токи ветвей через контурные токи I₁ I₁₁ и токи нагрузок I_1, I₂ I₃.

Подставим в (3.2) значения токов ветвей, выраженные через контурные и нагрузочные токи (3.1):

Введем понятия собственных сопротивлений контура Z_ii (сумма сопро­тивлений всех ветвей контура i) и взаимных сопротивлений контуров i и j Z_ij (сопротивление ветвей, входящих одновременно в контуры i и j). Знак взаим­ного сопротивления Z„ выбирается при сопоставлении направлений контур­ных токов I_i и I_j , если в ветви Z_ij направления токов совпадают, то сопротив­ление Z_ij имеет знак плюс, при встречном направлении токов - знак минус. Таким образом, для (3.3):

Теперь система контурных уравнений может быть записана в более общем виде

Для сети, включающей k независимых контуров:

Система представляет собой каноническую запись контурных урав­нений, в которой А_i - свободные члены, i = 1,2,..., k, могут быть перенесены в правую часть уравнений.

Метод узловых напряжений

Рассмотрим вывод системы уравнений узловых напряжений для сети, схе­ма замещения которой показана на рис. На схеме приведены продольные проводимости ветвей сети Y_ij и поперечные проводимости ветвей, которые эк-

вивалентированы к узлам схемы сети и показаны в виде узловых шунтов Y_i . В узлах сети указаны линейные нагрузочные токи I_i , которые при выводе урав­нений узловых напряжений будем считать известными. Кроме указанных па­раметров для рассматриваемой сети задано напряжение базисного узла u_Б .

Целью составления уравнений узловых напряжений является установление связи неизвестных напряжений узлов сети с известными нагрузочными токами при помощи параметров схемы замещения сети. Покажем на схеме токи в вет­вях сети и токи шунтов и зададим их условные направления.

Запишем уравнения баланса линейных токов для всех узлов сети, кроме балансирующего узла, на основе I закона Кирхгофа с учетом условного на­правления токов:

Теперь все неизвестные линейные токи ветвей электрической сети выра­зим через напряжения узлов и проводимости ветвей:

Токи шунтов также выражаются через напряжения узлов и проводимости:

Далее

Система уравнений нелинейная по отношению к неизвестным на­пряжениям узлов сети. Точных методов решения систем нелинейных уравне­ний не существует, поэтому решение системы уравнений узловых напряжений в форме баланса мощностей может быть получено только на основе итераци­онного процесса.

Метод коэффициентов распределения.

Метод основан на понятии коэффициента распределения w• - доли уча­стия нагрузки узла i в токе или потоке мощности ветви q схемы замещения сети. В общем виде коэффициент распределения является комплексной величинойа совокупность коэффициентов образует матрицу W. Матрица коэффициентов распределения W— прямоугольная с числом строк, соответствующим числу ветвей схемы замещения сети, и числом столбцов, равным числу узлов сети без балансирующего. Если электрическая сеть состоит из т ветвей и п узлов без ба­лансирующего узла, тогда матрица коэффициентов распределения W имеет вид:

Ток J_q в ветви q может быть представлен в виде линейной комбинации нагрузочных токов I_i :

Метод разрезания контуров.

Метод разрезания контуров сводится к размыканию контуров сложно-замкнутой сети по любым узлам и расчету режима полученной разомкнутой схемы. Параметры установившегося режима сложнозамкнутой сети будут идентичны параметрам режима разомкнутой сети, если напряжения в точках разреза одинаковы.

Рассмотрим сложнозамкнутую сеть, приведенную на рис. Сеть со­стоит из двух независимых контуров, размыкая которые по любым узлам, на­пример, по узлам 2 и 3, можно перейти к разомкнутой схеме (см. рис. б). Нагру­зочные токи I₂ и I₃, при этом разносятся соответственно по узлам 2', 2" и 3', З":

Нагрузочные токи можно распределить между точками разрыва произ­вольно или исходя из инженерных соображений, что ускоряет сходимость ите­рационного процесса.

Вследствие произвольности распределения нагрузочных токов I₂ и I₃ на­пряжения в фиктивных точках разрезания контуров не будут одинаковы, т. е.:

Найденные различия векторов напряжений называются невязками напря­жений или фиктивными контурными ЭДС. Для ликвидации невязок напряже­ний можно определить уравнительные токи в контурах сети I_ур1 I_ур2. Их величина определяется значениями ЭДС (6.1). В общем случае следует учиты­вать взаимное влияние контуров и определять уравнительные токи на основе контурных уравнений. Однако с учетом итерационного характера решения можно пренебречь взаимным влиянием контуров и определить уравнительные токи для каждого контура независимо. При этом взаимное влияние может быть ослаблено с помощью коэффициента торможения — k_т что ускоряет процесс сходимости:

где Z_л1 и Z_л11 — собственные сопротивления контуров.

Найденные уравнительные токи накладываются в точках разреза и коррек­тируют распределение нагрузочных токов, т. е. новое приближение распреде­ления нагрузочных токов вычисляется как:

Итерационный процесс повторяется до достижения требуемой точности расчета напряжений в узлах разрыва, т. е. до необходимого уменьшения невязок напряжений.