Voprosy_i_otvety_k_gosam / 44 кз

3.4. Расчет несимметричных КЗ. Метод симметричных составляющих.

Виды несимметрии: поперечная, продольная, однократная, многократная.

В трехфазных сетях могут возникать следующие виды несимметричных КЗ: двухфазное, однофазное, и двухфазное на землю.

Для определения токов, проходящих при несимметричных КЗ, применяют метод симметричных составляющих, сущность которого состоит в том, что любую несимметричную трехфазную систему векторов (токов, напряжений) можно представить в виде трех симметричных систем. Одна из них имеет прямую последовательность чередования фаз , другая – обратную. Система нулевой последовательности состоит из трех равных векторов, совпадающих по фазе. Т. о. для каждой фазы можно записать:

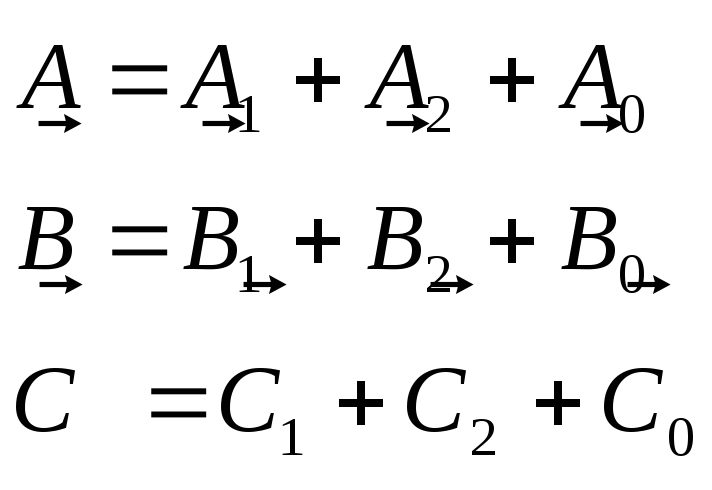
Поперечная – несимметричные КЗ

продольная – обрыв одной или двух фаз одновременно

“1” “2” “0”

трехфазная система векторов симметричных составляющих

вращающиеся векторы.

=

-матрица симметричных составляющих - дает возможность определить значения величин в фазах (по умолчанию если определенны значения прямой обратной нулевой последовательности для фазы А)

Зная значения I или U в месте повреждения можно определить значения этих же величин для разных последовательностей (по умолчанию фазы А)

Замечание:

При использование метода симметричных составляющих не учитываются ЭДС Е2 Е0 , для СМ которые обусловлены появлением токов соответственно обратной и нулевой последовательности

Допущение для расчета несимметричных токов КЗ

1. В нормальном режиме или при 3-х фазном КЗ, существуют только составляющие прямой последовательности

2. В симметричных цепях I U различных последовательностей не взаимодействуют с друг другом.

Сост. разные сх. замещения “1” “2” “0” рассчитывается каждая в отдельности, а величины находятся методом наложения

3. Каждый элемент электрической системы Z1 Z2 Z0 имеет свое сопротивление

Сх№1

Еi

Uki

Сх№2

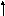
Для расчета несимметричных режимов сх№1 преобразовывается в сх№2.

Uki-остаточное U какой-то последовательности , которая определяется для повреждения (поперечная несимметрия), если мы рассм продольную несимметрию то сх замещения имеет следующий вид

-падение напряжения в точке несимметрии

В связи с указанными трудностями в практических расчетах обычно довольствуются лишь учетом основных гармоник токов и напряжений, что в большинстве случаен является приемлемым с точки зрения допустимой погрешности.

Если известны сопротивления электроустановки токам различных последовательностей, т.е. известны так называемые сопротивления прямой, нулевой, обратной последовательностей, то можно для точки несимметрии записать;

При учете источников в уравнения следует ввести ЭДС соответствующих после­довательностей, Известно, что в СМ возникают ЭДС всех последовательностей: обратной и нулевой являющихся реакцией СМ на протекание в статоре токов нулевой обратной последовательностей. Таким образом, ЭДС и удобнее учитывать в форме падения напряжения. При этом принято считать, что АРВ всех СМ реагируют только на основную гармонику, т.е. включены через фильтр прямой последовательности.

Итак, для режима с поперечной несимметрией можно записать;

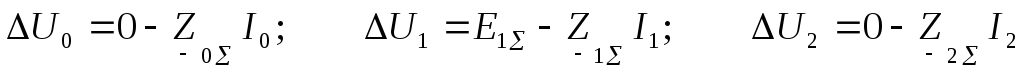
Так как уравнения для различных последовательностей независимы друг от друга, то при определении ЭДС и 'эквивалентных сопротивлений можно составлять три схемы замещения для каждой из последовательностей в отдельности.

Уравнения для прямой последовательности содержат поэтому ток течет от источника ЭДС в точку несимметрии. Токи же и текут из точки несимметрии.

4.2. Анализ однофазного короткого замыкания с использованием граничных условий в месте несимметрии А. Правило эквивалентности тока прямой последовательности

Предполагается, что кз произошло в фазе А.

Запишем граничные условия

В точку кз, ток протекает только из поврежденной фазы, а напряжения не равны нулю в фазах В и С.

Запишем для фазы А

Применив обратную матрицу коэффициентов получим

Далее, подставив вместо и ток просуммируем раздельно левые и правые части уравнений Кирхгофа получим;

,

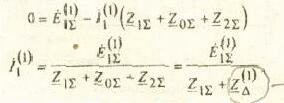где -

Ток в поврежденной фазе в месте кз. будет равен

Определим ток и напряжения других последовательностей по

Построим для случая чисто индуктивной схемы векторные диаграммы (рис.4.3).

При расчетах токов и напряжений в точке несимметрии для различных видов несимметрии величина определяется формулой, которая приведена ниже.

Здесь и - обрыв одной и двух фаз соответственно, увеличение сопротивления в фазе на величину Z

Векторная диаграмма при двухфазном КЗ на землю.

Векторные диаграммы при двухфазном КЗ.