5. Выбор числа цепей и сечений проводов лэп при проектировании (экономическая плотность тока, метод экономических интервалов)

Для выбора числа цепей и сечений проводов ЛЭП (без учета фактора надежности) нашли применение два метода: экономической плотности тока и экономических интервалов. Хотя первый из них уступает в точности расчета второму, но благодаря простоте применения продолжает пользоваться популярностью у инженеров.

Метод экономической плотности тока основан на линейной аппроксимации действительной дискретной зависимости удельных капиталовложенийK₀ в сооружение ЛЭП от ее сечения F. На рис. приведен пример такой аппроксимации для воздушной линии (ВЛ) 110 кВ.

Линейная аппроксимация K₀ вида: соответствует увеличению капиталовложении с ростом сечения провода. Здесь а – кап. вложения в 1 км линии, не зависящие от сечения,b – часть удекап.вложений, пропорциональная сечению провода. Однако одновременно уменьшается стоимость И_W потерянной энергии при передаче мощности по ЛЭП. Если обозначить максимальную расчетную перспективную электрическую нагрузку ЛЭП через Р_мах, число часов максимальных потерь , то при выбранном номинальном напряжении ЛЭП Uном ВЛ 110 кВ и их аппроксимация и известных коэффициенте мощности cos нагрузки и стоимости  единицы годовой потерянной энергии W имеем следующие соотношения: ,

где И_W - удельные годовые издержки на компенсацию потерянной энергии,  - удельное сопротивление проводов ЛЭП. Все данные приведены на единицу длины (1 км) ЛЭП. Объединяя записанные выше соотношения, имеем: .

Где I – наибольший рабочий ток линии, τ – время наибольших потерь

О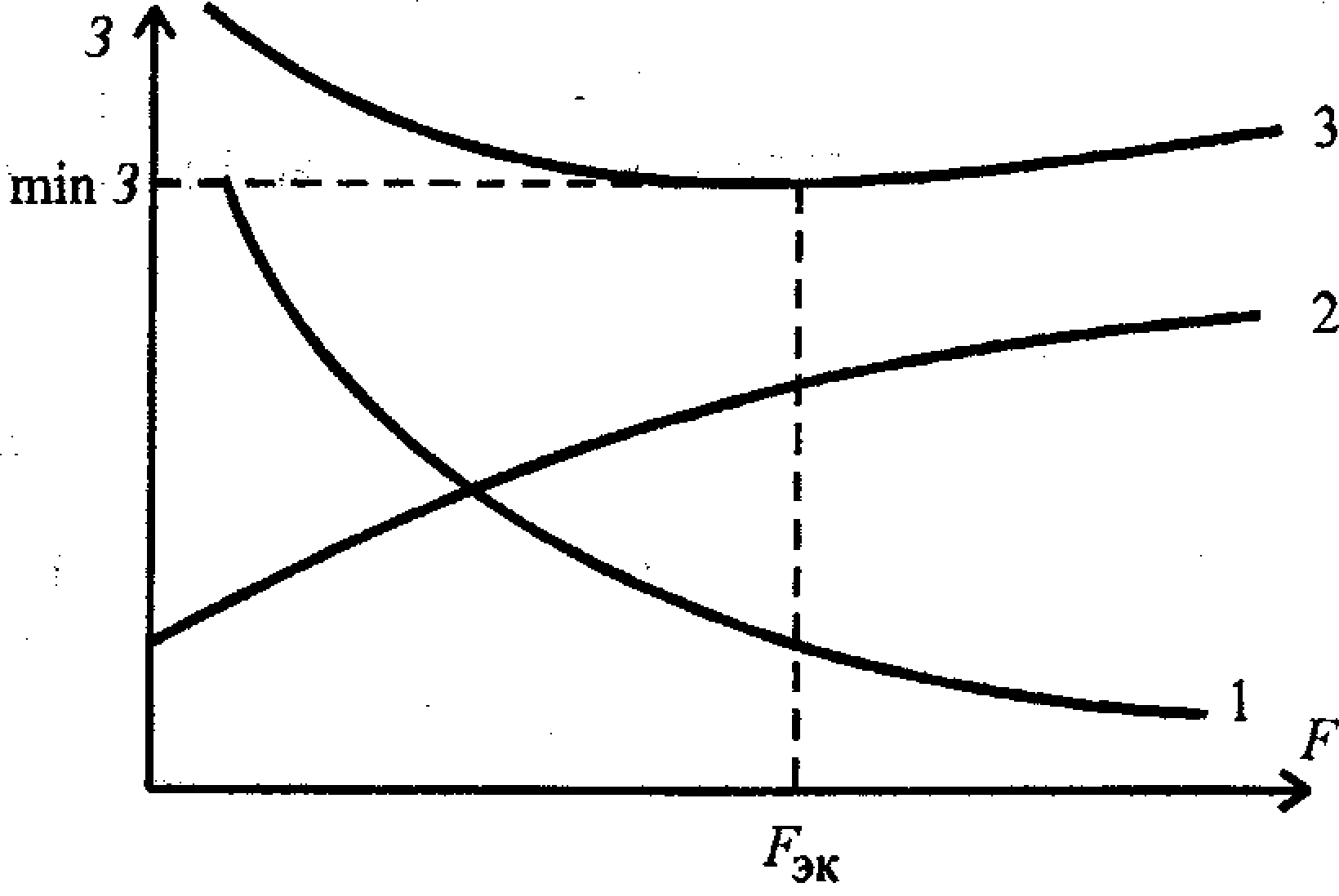пределяя ежегодные амортизационные отчисления И_ам и издержки на обслуживание ЛЭП И_обс как известные доли отчислений от капиталовложений _ам и _обс соответственно, в удельном выражении имеем: .

В качестве критерия выбора сечения проводов ЛЭП целесообразно принять экономический критерий минимума годовых приведенных затрат З, которые для единицы длины ЛЭП определяются формулой:

Возможность расчетов через удельные величины обосновывается линейной зависимостью от длины ЛЭП всех членов последней формулы. Объединяя все имеем выражение:

Первое слагаемое определяется капиталовложениями в ЛЭП и прямо пропорционально сечению проводов, а второе - издержками на потери энергии и обратно пропорционально сечению см. рис. Наивыгоднейшее (экономическое) сечение провода Fэк соответствует минимуму функции З₀. В результате получаем:. (*)

Введя понятие экономической плотности тока j_эк = I_мах/F_эк , соответствующей экономическому сечению(отношение наибольшего протекающего в линии тока к экономическому сечению), вместо (*) можно записать:(**).

Выражение (**) позволяет определить экономическое сечение при любой расчетной нагрузке. Примечательно, что j_эк от величины нагрузки не зависит. Учитывая, что в (**) все, коэффициенты, кроме , мало изменяются при изменении исполнения ЛЭП, экономическую плотность тока можно рассчитать заранее и нормировать лишь в зависимости от .

Серьезными недостатками метода экономической плотности тока являются неучет дискретности сечений проводов (в результате чего найденное экономическое сечение надо округлять до ближайшего стандартного) и погрешность самой линейной аппроксимации. Особенно велика эта погрешность, когда рассматривается широкий диапазон передаваемых мощностей и рассматривается возможность сооружения нескольких цепей ЛЭП.

Указанных недостатков лишен метод экономических интервалов. Основываясь на том же методе годовых приведенных затрат, что и метод экономической плотности тока, этот метод использует непосредственные зависимости затрат от передаваемой мощности (или тока), полученные для фиксированных сечений проводов. В удельном выражении они имеют вид:(***),

где индекс i указывает порядковый номер суммарного сечения фазы электропередачи при ранжировке сечений в порядке возрастания F₁ <F₂ <..., Постоянная часть затрат соответствует первому слагаемому, второе слагаемое соответствует стоимости потерь электроэнергии И_{W и зависит от квадрата тока, поэтому кривые приведенных затрат - параболы.}

Видно, что выражение (***) квадратичное, имеющее вид: .

Т. к. с увеличением сечения с_i обычно возрастает, а d_i уменьшается, то изображение семейства характеристик затрат на диаграмме (рис. ) будет иметь вид взаимно-пересекающихся кривых: Если построить эти; кривые на графике, то задачу выбора сечений легко решать графически. Например, при любом заданном токе надо найти кривую с наименьшей ординатой и выбрать соответствующее ей сечение. Очевидно, что геометрическое место таких ординат - это нижняя огибающая семейства кривых приведенных затрат. Эта огибающая носит название функции оптимальных затрат в ЛЭП.

Использование графического метода для определения экономических сечений проводов ЛЭП наглядно, но неудобно. В справочной литературе заранее рассчитанные экономические интервалы приводятся в табличной форме.