КВАНТЫ билеты / Энергетический спектр и волновые функции стационарных состояний водородоподобного атома

Энергетический спектр и волновые функции стационарных состояний водородоподобного атома

Для того, чтобы указать стационарное состояние электрона в атоме, используют специальную комбинацию двух символов. В ней первым символом является число, равное значению главного квантового числа n, которое нумерует стационарное состояние, вторым – малая буква из латинского алфавита, соответствующая орбитальному квантовому числу l по

схеме:

s l 0 , p l 1,

d l 2 и т.д.

Например, состояние, которое характеризуется квантовыми числами n 0 и l 0, обозначается символом 1s .

При заданном главном квантовом числе n наименьшее значение орбитального квантового числа l есть нуль, а наибольшее соответствует случаю, когда nr = 0, следовательно, оно равно n – 1. В связи с этим число l изменяется следующим образом: l = 0, 1, 2, … , (n – 1). Отсюда приходим к выводу, что существует n стационарных состояний, которые отличающихся значением квантового числа l, но имеют одинаковое значение квантового числа n. Причем при фиксированном значении орбитального квантового числа l магнитное орбитальное квантовое число ml может принимать (2l + 1) различных значений (было показано в п. 5.3). Другими словами, имеется (2l + 1) стационарных состояний с различными значениями ml и одинаковым значением l.

Из формулы (6.23) для энергии электрона, движущегося в кулоновском поле водородоподобного атома, видно, что его энергия Еn в стационарных состояниях зависит только главного квантового числа n. Поэтому значения энергии электрона в стационарных состояниях, которые характеризуются одинаковым значением n, но различными значениями l и ml, одни и те же. Это означает, что n-й энергетический уровень, за исключением первого (основного) n = 1, является вырожденным.

При этом надо помнить, что каждый n-й уровень вырожден по квантовому числу l с кратностью n, в свою очередь каждый l-й подуровень вырожден по квантовому числу ml с кратностью (2l + 1). Таким образом, общая кратность вырождения n-го энергетического уровня равна

водородоподобного атома, на которой изображены два энергетических

Рис. 6.2

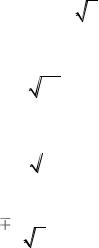
уровня, соответствующих пяти стационарным состояниям. Квадратиками отмечены квантовые ячейки – символическое изображение орбиталей.

Используя выражения (6.24) для радиальной функции Rn,l (r) и (5.54) для сферической функции Yl,ml ( , ) , найдем явный вид нормированных собственных функций n,l,ml ( r , , ) электрона, который находится в

стационарных состояниях в водородоподобном атоме. Запишем орбитали (6.26), для нескольких случаев, а именно, когда электрон находится в 1s-, 2s- и 2p-состояниях:

В соответствии с четвертым постулатом квантовой механики вероятность dPn,l,ml (r, , ) того, что при измерении положения электрона в

квантовом состоянии, характеризуемом числами n, l и ml, он будет обнаружен в малом объеме dV r2dr sin d d около точки с координатами ( r, , ), определяется выражением

другими словами, эта формула дает распределение вероятности в радиальном направлении.

В случае интегрирования вероятности (6.29) по радиальной переменной r от 0 до приходим к угловой зависимости вероятности dPl,ml ( , ) , иначе

вероятности того, что электрон окажется где-то в пределах элемента телесного угла d sin d d около луча, задаваемого углами ( , )

состояниям электрона в водородоподобном атоме. Электронная плотность уменьшается с увеличением расстояния от ядра, но теоретически равна нулю только на бесконечном от него расстоянии. В сторону ядра плотность уменьшается еще более резко и вблизи него практически равна нулю.

Наглядную пространственную картину о положении электрона в атоме может дать изображение электронного облака. Под ним понимают область пространства, в каждой точке которой может находиться электрон. На рис. 6.4. показаны сечения электронных облаков плоскостью, проходящей через ядро, для двух простых случаев: электрон в водородоподобном атоме находится в 1s- и 2s-состояниях. Видно, что электронные облака отличаются

по размеру, форме и распределению плотности. Кроме того, электронные облака не имеют четких границ, края их размыты в пространстве. Электронное облако для 2s-состояния, будучи также, как и все s- облака шарообразным, является двухслойным.

Размеры электронных облаков зависят от заряда