
КВАНТЫ билеты / 17. Частица в потенциальном силовом поле прямоугольной формы
.pdf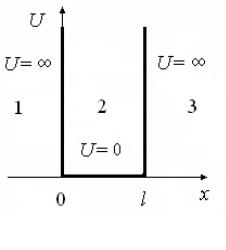
Частица в потенциальном силовом поле прямоугольной формы
Если микрочастица движется в поле, потенциал которого в некоторых местах может существенно меняться при малом изменении расстояния (меньших, чем длина λ волны де Бройля частицы), то должны проявляться квантовые эффекты. Это означает, в частности, что спектр оператора Гамильтона не сплошной, а точечный, т. е. собственными значениями
оператора ˆ могут быть числа только из дискретного множества. В этом
H
случае говорят, что энергия квантуются. Далее будем исследовать движение частицы в потенциальных полях, имеющих прямоугольную форму, т. е. когда изменение потенциала в заданных точках пространства происходит скачкообразно. Хотя такие прямоугольные формы не встречаются в природе (реальные потенциалы не имеют разрывов), тем не менее, их можно использовать с целью приближенного изучения поведения квантовой частицы в реальных потенциальных полях.
Прямоугольная потенциальная яма с бесконечным скачком потенциала. Исследуем поведение микрочастицы массы m в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Предположим, что она движется вдоль координатной оси X, но ее движение ограничено двумя непроницаемыми стенками с координатами х = 0 и х = l. Потенциальная энергия U(х) частицы должна удовлетворять требованиям:
|
|
|
|
|
|
|
|
|
|
||
0, |
при |
0 x l |
, |
|
|
||||||
U (x) |
|
|
|
x 0 , |
l x . |
|
|||||
, |
|
при |
|
||||||||
|
|
|
|
|
|
|
|
|
|
||
Зависимость потенциальной энергии U(х) от |
|
||||||||||
координаты x изображена на рис. 4.1. Назовем |
|
||||||||||
интервал х ≤ 0 областью 1, интервал 0 < х < l |
|
||||||||||
областью 2 (потенциальной ямой ширины l), а |
|
||||||||||
интервал х ≥ l областью 3. |
|
|
|
|
|
|
|||||
Рассматривая данную задачу в координатном |
|
||||||||||
представлении, важным |
этапом |
становится |
Рис. 4.1 |
||||||||
решение стационарного |
уравнения |
Шредингера |
|||||||||
|
|||||||||||
(3.32), которое в одномерном случае примет вид |
|
||||||||||
|
d 2 |
|
|
(x ) |
2m |
[E U (x)] (x ) = 0 . |
(4.8) |
||||
|
|
|
|
|
|||||||
|
dx2 |
|
E |
|
2 |
|
E |
|
|||
|
|
|
|
|
|
|
|||||
Прежде чем решить это уравнение, отметим следующее. За пределы потенциальной ямы, т. е. в области 1 и 3, частица попасть не может, поэтому вероятность ее обнаружения там равна нулю. Значит, и E (x )-функции в этих
областях будут равны нулю. Из свойства непрерывности E (x )-функции

следует, что она должна равняться нулю на границах потенциальной ямы. Поэтому имеем следующие граничные условия:
E (0 ) = 0 и E (l ) = 0 . (4.9)
В области 2 E (x )-функция не равна нулю. Для этой области перепишем стационарное уравнение Шредингера (4.8)
|
|
|
d 2 |
|
(x ) + k 2 |
(x ) = 0 , |
|
|
|
|
|||
|
|
|
dx2 |
E |
|
E |
|
|
|
|
|
|
|
где k 2 |
2m |
E . |
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
|
||
Решение данного однородного дифференциального уравнения второго порядка с постоянными коэффициентами ищем в виде E (x ) = eγx. После его
подстановки в уравнение имеем: γ1,2 = ±ik. Поэтому общее решение уравнения можно записать следующим образом
E (x ) c1 sin kx c2 coskx . |
(4.10) |
где с1 и с2 – это неопределенные пока постоянные.
С помощью граничных условий (4.9) найдем вид E (x )-функции,
удовлетворяющей этим условиям.
Когда х = 0, выполняется равенство E (0 ) = c1 sin 0 c2 cos0 0 . Из него
следует, что коэффициент с2 = 0, поэтому E |
(x ) c1 sin kx. |
|
|||
Если х = l, |
то получается равенство |
E (l ) c1 sin kl 0 , из |
которого |
||
следует, что при |
любом ненулевом значении с1 требуется выполнение |
||||
sin kl 0 . Последнее равенство справедливо при kl n или k |
n |
, где n = |
|||
l |
|||||
|
|
|
|
||
1, 2,… . Значение |
n = 0 исключается, поскольку приводит к результату E (x ) |
||||
= 0 при любых значениях x из области 2, а это соответствует случаю, когда частица отсутствует в потенциальной яме.
Итак, E (x )-функция n-го стационарного состояния частицы, находящейся в области 2, определяется выражением
E (x ) c1 sin nl x n (x) ,
зависящим от n. Значение коэффициента с1 получают из условия нормировкиn (x )-функции:
l |
|
l |
n x |
|
понижаем |
|
|
|
|
l |
cos(2n x / l) |
|
|||||||||
|
|
|
|
|
|
|
|||||||||||||||
| n (x) |2dx c12 sin 2 |
dx |
|
|
c12 |
|
1 |
dx 1 . |
||||||||||||||
|
степень |
|
|
|
|
|
|
||||||||||||||
0 |
|
0 |
l |
|
|
|
|
0 |
|
|
|
2 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l / 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Поэтому, нормировочный множитель равен |
|
|
c |
|
2 |
|
. В итоге, приходим к |
||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
l |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
нормированной n (x )-функции, описывающей стационарные состояния, |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|||||
|
|
|
|
(x) |
2 |
|
sin |
x . |
|
|
|
|
|
(4.11) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
n |
|
|
l |
l |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
На рис. 4.2 приведены графики этих n (x )- |
|
|
|
|
|
|
|
||||||||||||||
функций для первых двух стационарных |
|
|
|
|
|
|
|
||||||||||||||
состояний (n = 1 и n = 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Чтобы найти значения полной энергии E |
|
|
|
|
|
|
|
||||||||||||||
частицы |
в |
стационарных |
состояниях, |
|
|
|
|
|
|
|
|||||||||||
воспользуемся равенством
|
2 |
n 2 |
|
2m |
|
||
k |
|
|
|
|
|
|
E |
|
|
2 |
|||||
|
|
|
l |
|
|
|
|
Откуда следует, что
E En 2 2 n2 2ml 2
.
. (4.12)
Таким образом, граничным условиям (4.9) удовлетворяют только такие состояния частицы, для которых значения En полной энергии Е образуют дискретный ряд. Это означает, что полная энергия Е частицы, находящейся в потенциальной яме, может иметь лишь квантованные значения En, зависящие от n-го состояния частицы. Целое
положительное число n, нумерующее стационарные состояния и определяющее значение энергии частицы,
называется квантовым числом.
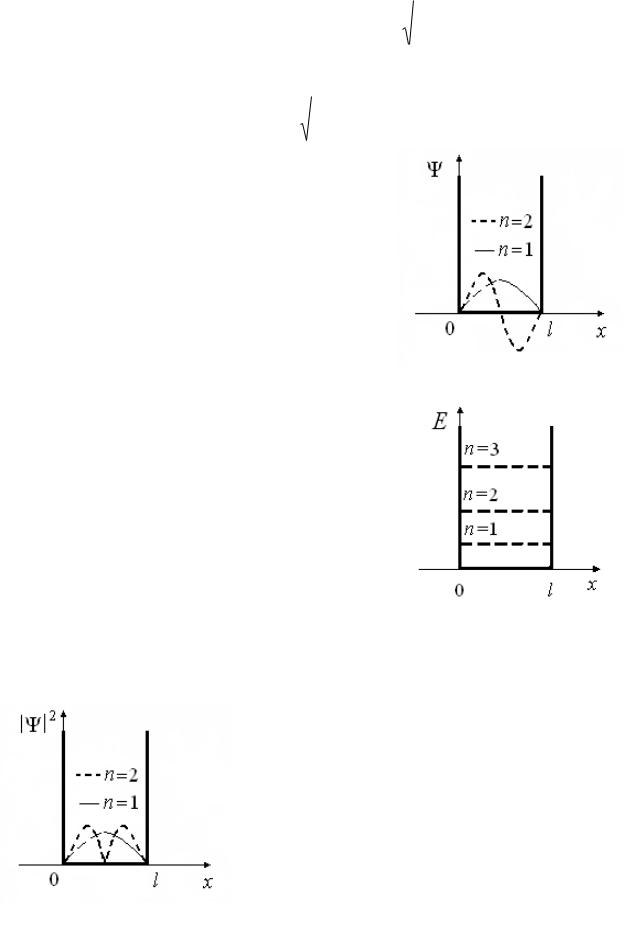
Энергетический спектр частицы в прямоугольной потенциальной яме схематически показан на рис. 4.3 системой
энергетических уровней. Отметим, что расстояние Еn между соседними уровнями с ростом n будет возрастать
Рис. 4.4
En En 1 En 2 2 (2n 1) . 2ml 2
Плотность вероятности обнаружения частицы, находящейся в n-м состоянии, в определенном месте потенциальной ямы, характеризует квадрат
модуля |
|
(x) |
|
2 |
функции |
(x) . На рис. 4.4 представлены графики |
|
(x) |
|
2 |
|
|
|
|
|||||||
|
|
n |
|
|
|
n |
|
n |
|
|
для состояний с n = 1 и n = 2. Из них видно, что вероятность обнаружения частицы в потенциальной яме зависит как от ее состояния, так и от места обнаружения.
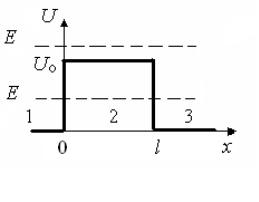
Прямоугольный потенциальный барьер. Рассмотрим прохождение микрочастицы с массой m и полной энергией Е через одномерный прямоугольной потенциальный барьер конечной высоты Uo и ширины l. Пусть координатная ось X сонаправлена с направлением движения частицы. Предположим, что движение происходит в силовом поле, в котором изменение потенциальной энергии U(х) частицы от x происходит согласно рис. 4.5. В этом случае потенциальная энергия U(х) частицы определяется как
U |
0 |
, при 0 x l , |
|
|
|
|
|
U (x) |
|
|
|
|
|
при x 0 , |
l x . |
0, |
|
||
Назовем интервал х ≤ 0 областью 1, интервал 0 < х < l областью 2
(прямоугольным потенциальным барьером
высоты Uo и ширины l), а интервал х ≥ l областью 3.
Считаем, что квантовая частица начинает движение из области 1. Для нее, в отличие от классической частицы, всегда имеется некоторая вероятность того, что при Е < Uo она пройдет через потенциальный барьер и окажется в области 3 (это явление называется
«туннельный» эффект), а при Е > Uo частица отразится от барьера и обнаружится в области 1. Характеризуют эти вероятности такие величины как коэффициент прозрачности D потенциального барьера и коэффициент его отражения R.
Коэффициент прозрачности D равен вероятности прохождения частицы сквозь потенциальный барьер и может быть определен как отношение плотности потока Iпр в прошедшей сквозь барьер волне де Бройля к плотности потока Iпад в падающей на барьер волне: D = Iпр / Iпад.
Коэффициент отражения R – это вероятность того, что частица испытает отражение от потенциального барьера, он равен отношению
плотности потока Iотр в отраженной от барьера волне де Бройля к плотности
потока Iпад в падающей на барьер волне: R = Iотр / Iпад.
Причем, для этих коэффициентов выполняется следующее равенство: D + R = 1, так как сумма D и R дает вероятность достоверного события – частица либо пройдет через барьер, либо отразится от него.
Чтобы найти коэффициенты D и R, нужно вначале решить стационарное уравнение Шредингера вида (4.8)
d 2 |
|
(x ) |
2m |
[E U (x)] |
|
(x ) = 0 . |
|
|
E |
||||
dx2 |
E |
|
2 |
|
||
|
|
|
|
|||
Поскольку здесь потенциальная энергия U(х) является разрывной функцией, это уравнение необходимо решить для каждой из областей 1, 2 и 3 в отдельности. Решениями будут функции, описывающие состояние частицы в этих областях, которые обозначим через 1 (x ), 2 (x ) и 3 (x ). Для данных
функций, в соответствие со свойством непрерывности Ψ-функции и ее первой производной (x) по координате х на границах областей, где
происходит конечный скачок функции U(х), напишем следующие граничные условия:
1 |
(0) |
2 |
(0) |
и |
2 |
(l) 3 |
(l) |
. |
(4.13) |
||
|
(0) |
|
(0) |
|
|
(l) |
(l) |
||||
|
|
|
|
|
|||||||
1 |
|
2 |
|
|
2 |
3 |
|
|
|
||
Часто представляет интерес случай, когда полная энергия Е частицы меньше высоты потенциального барьера Uo (Е < Uo). Поэтому ограничимся рассмотрением именно этого случая.
Напишем стационарное уравнение Шредингера для областей 1, 2 и 3:
d 2 |
(x) k 2 |
(x) 0 |
, |
|
где k 2 |
2m |
E , |
|
|
|||||||||
|
|
|
|
|
|
|
|
|||||||||||
dx2 |
|
|
|
1 |
|
1 |
|
|
|
|
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
d 2 |
|
|
(x) 2 |
(x) 0 |
, |
где 2 |
|
2m |
(U |
|
E) , |
||||||
|
|
|
|
|
|
0 |
||||||||||||
|
dx2 |
|
2 |
|
2 |
|
|
|
|
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
d |
2 |
|
(x) k 2 (x) 0 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
dx2 |
3 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Общие решения этих уравнений запишем соответственно в виде
1(x) a1eikx b1e ikx ,
2 (x) a2e x b2e x ,

3 (x) a3eikx b3eikx a3eikx .
0
Слагаемые в выражениях для волновых функций 1 (x ) и 3 (x ) характеризуют
волны де Бройля, которые распространяются в противоположных направлениях. Например, в выражении для 1 (x ) первое слагаемое
соответствует падающей волне с амплитудой а1, а второе слагаемое – отраженной волне с амплитудой b1. В области 3 нет отраженной волны, поэтому второе слагаемое в выражении для 3 (x ) равно нулю.
Экспоненциальные слагаемые ex , входящие в |
|
2 |
(x ), являются |
|
|
|
действительными функциями.
Исходя из определения коэффициентов D и R, а также, учитывая, что плотность потока в падающей волне де Бройля пропорциональна произведению волнового числа k и интенсивности волны (равной квадрату
модуля |
|
a |
|
2 |
ее амплитуды a ), |
|
в прошедшей волне пропорциональна: k |
|
a |
|
2 |
, |
||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
а в отраженной: k |
|
b |
|
2 |
, для D и R можно написать следующие равенства |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
3 |
|
2 |
|
|
|
|
b |
|
2 |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
|
и R |
|
|
|
1 |
|
|
|
|
. |
(4.14) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
a |
|
2 |
|
|
|
a |
|
|
|
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
||
Следовательно, для того чтобы вычислить коэффициенты D и R необходимо найти значения а1, b1 и а3. Воспользуемся для этого граничными условиями (4.13).
При х = 0 имеем:
a1 b1 a2 b2 ,
ika1 ikb1 a2 b2 .
При х = l:
a2el b2el a3eikl ,
a2el b2e l ia3 k eikl .
Разрешая эту систему из четырех уравнений, приходим к следующим выражениям для коэффициентов прозрачности D и отражения R:
|
|
(k 2 2 )2 sh 2 l 1 |
|
|
||||
D 1 |
|
|
|
|
|
|
, |
(4.15) |
|
2 |
|
2 |
|||||
|
|
4k |
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
4k 2 2 |
|
|
|
1 |
|
||||
|
|
|
|
|
|
|
|||||||
R 1 |
|
|
|
|
|
|
|
|
|
|
. |
(4.16) |
|
|
2 |
|
2 |
|
2 |
|
2 |
|
|||||
|
|
(k |
|
) |
sh |
|
|
|
|
||||
|
|
|
|
|
|
l |
|
|
|||||
Здесь использовали гиперболический синус sh( l) |
e l e l |
||
|
, для которого |
||
2 |
|||
|
|
||
выполняется равенство sin(i l) i sh( l) . |
|
|
|
Таким образом, при выполнении условия Е < U0 получаем неравенства D > 0 и R < 1 (отметим, что для классической частицы всегда справедливы равенства D = 0 и R = 1). Значит, частица проходит за барьер и при энергиях Е меньших, чем его высота U0 . Коэффициент D монотонно убывает с ростом ширины l барьера и не обращается в нуль при конечных значениях l.
Аналогичные вычисления без особых трудностей проводятся когда Е > U0. В этом случае выполняются следующие неравенства: D < 1 и R > 0 (для классической частицы: D = 1 и R = 0).
