КВАНТЫ билеты / 17.Простейшие приложения стационарной теории возмущений

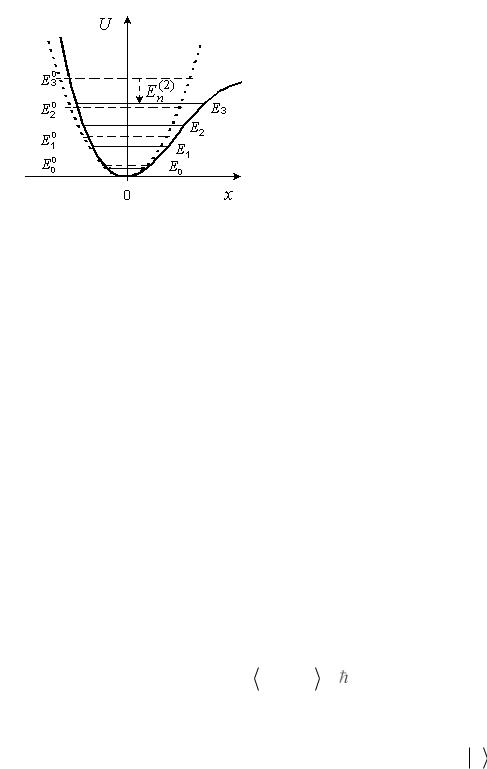
Простейшие приложения стационарной теории возмущений

Для того чтобы проиллюстрировать основные положения п. 7.1, рассмотрим применение метода теории стационарных возмущений на двух простых примерах, в одном из которых упрощенная система имеет не вырожденные энергетические уровни, а в другом – вырожденные.

Ангармонический осциллятор. В п. 4.3 было проведено изучение одномерного линейного гармонического осциллятора, решено стационарное уравнение Шредингера и найдены его точные решения. Однако такой осциллятор является модельной идеализацией реальных колебательных систем, поскольку действительный гамильтониан

ˆ , строго говоря, не представляется

H

выражением (4.18), а имеет более сложный вид.

Для потенциальной энергии зависимость U(x) не является параболой (см. рис. 7.1), так как при разложении U(x) в ряд Тейлора по степеням отклонения x от положения равновесия необходимо учитывать кроме

члены разложения. Если считать эти дополнительные члены малыми, то можно использовать теорию возмущений, а добавочные члены в разложении U(x) будут являться поправками к гармоническому приближению и описывать ангармоничность колебаний.

Напомним, что для гармонического осциллятора оператор Гамильтона

ˆ 0 записывается в виде (4.18)

H

и зависит от колебательного квантового числа n (рис. 7.1.). Собственные

векторы ˆ 0 в представлении Фока были обозначены как .

H n

Будем учитывать в разложении потенциальной энергии U(x) еще и кубический член вида x3 , где – вещественное безразмерное число, много меньшее единицы, называется коэффициент ангармоничности

Поэтому, достаточно вычислить ненулевые матричные элементы матрицы

оператора ˆ .

V

Принимая во внимание формулу (4.33), произведем в выражении (7.25) замену оператора xˆ на

действие каждого члена оператора ˆ , стоящего в квадратных скобках, на

V

кет-вектор n .

Учитывая (4.39б), запишем

(aˆ )3 n(n 3)(n 2)(n 1) n 3 .

Из (4.39а) следует

(aˆ)3 nn(n 1)(n 2) n 3 .

Несложно получить и следующие равенства:

Таким образом, отличными от нуля будут только недиагональные матричные

элементы оператора ˆ :

V

второго приближения вычисляется просто, так как в сумме по индексу k (см. 7.27) присутствуют только четыре члена (7.29) и (7.30): k n 3 и k n 1.

каждого энергетического уровня гармонического осциллятора на величину, равную поправке во втором приближении En(2) (рис. 7.1). При этом чем больше квантовое число n , тем сильнее смещение. Уровни энергии En уже

не являются эквидистантными, а расстояние между ними уменьшается с ростом числа n

Подстановка (7.29) и (7.30) в (7.28), позволяет найти в первом приближении выражение для собственного вектора nan ангармонического

осциллятора с учетом члена x3 .

Эффект Штарка в водородоподобном атоме. Если поместить атом во внешнее электрическое поле, то под действием этого поля энергия электрона, находящегося в стационарном состоянии, изменится. Это явление называется эффектом Штарка. Рассмотрим данный эффект на примере

водородоподобного атома, помещенного во внешнее постоянное однородное

электрическое поле напряженности E .

В п. 6.3 задача об энергетическом спектре и стационарных состояниях электрона (без учета спина и релятивистских эффектов) в кулоновском поле ядра водородоподобного атома была решена точно. В стационарных

а также операторов lˆ2 и lˆz , энергия электрона может принимать значения

(6.23)

Энергия зависит от главного квантового числа n , а каждый энергетический уровень En0 (исключая уровень с n 1) является вырожденным с кратностью, равной n2 .

ˆ

При включении поля E к оператору H0 добавляется оператор

радиус-вектором, проведенным от ядра к электрону), которая равна их скалярному произведению с обратным знаком:

Предполагаем электрическое поле такое, что дополнительная энергия мала по сравнению с расстоянием между соседними энергетическими уровнями атома, отличающимися числом n , но превышает расстояние между уровнями тонкой структуры, т. е. уровнями, обусловленными спин-орбитальным взаимодействием.

которого находится в состоянии, характеризуемом главным квантовым числом n 2. До включения электрического поля энергетический уровень

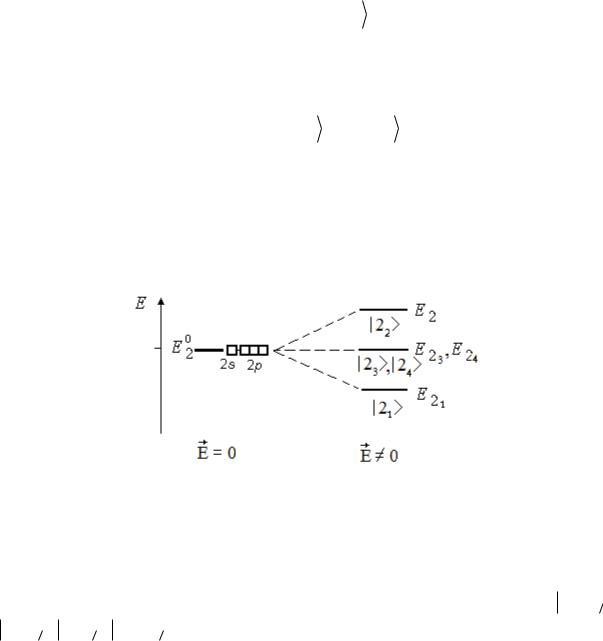
E20 является четырехкратно вырожденным (рис. 7.2).

Рис. 7.2

Энергией E20 обладает электрон, находящийся либо в одном 2s- состоянии, либо в каждом из трех 2p-состояний водородоподобного атома. Этим состояниям сопоставляются соответственно векторы состояний 2,0,0 и 2,1,0 , 2,1,1 , 2,1, 1 , которые определяются тремя квантовыми числами n , l и ml . Для удобства переобозначим эти векторы в соответствии со схемой:

первом порядке теории возмущения. При этом атом сможет находиться в

порядке теории возмущения представляется в виде линейной комбинации четырех векторов 2i0 , описывающих 2s- и 2p-состояния электрона в атоме

энергии в первом приближении.

В первом приближении, в соответствии с (7.23), имеем систему четырех однородных уравнений

Если функция (r) является четной, то выполняется равенство (7.38).

На основе данных определений получают следующее правило. Матрица нечетного оператора имеет отличные от нуля элементы только для состояний различной четности. Матрица четного оператора имеет не нулевые элементы

полярного вектора) нечетный, следовательно, его матрица имеет нулевые элементы для состояний одинаковой четности. В связи с этим, диагональный

матричный элемент ˆ равен нулю, поскольку для электрона в

2,0,0 d 2,0,0

водородоподобном атоме 2s-орбиталь является четной. Кроме того, три 2р-

нулю. Остальные шесть элементов могут быть отличными от нуля. Однако,

Определитель этой системы уравнений приравняем к нулю

Отсюда, получим уравнение 4-ой степени относительно E (1)

2 j

особых сложностей найти численное значение следующего матричного элемента декартовой координаты z

Итак, под действием электрического поля четырехкратно вырожденный энергетический уровень E20 расщепляется на три подуровня (рис. 7.2):

E23 = E24 = E20 .

Величина расщепления пропорциональна первой степени напряженности электрического поля, поэтому такое расщепление называется линейным эффектом Штарка. Один из подуровней, который соответствует

устанавливаем связь для величин eij , после чего, согласно (7.36), находим в

23 = e33 230 e43 204 ,

24 = e34 230 e44 204 ,

где числа e33 , e34 , e43 , e44 произвольны и не равны нулю.