KN_Vse_lektsii / algan16

Алгоритмический анализ. Лекция 16.

Программирование на Scheme

Бинарные деревья

Дерево — одна из наиболее широко распространѐнных структур данных в информатике, эмулирующая древовидную структуру в виде набора связанных узлов. Является связанным графом, не содержащим циклы. Большинство источников также добавляют условие на то, что рѐбра графа не должны быть ориентированными.

Узел является экземпляром одного из двух типов элементов графа, соответствующим объекту некоторой фиксированной природы. Узел может содержать значение, состояние или представление отдельной информационной структуры или самого дерева. Каждый узел дерева имеет ноль или более узлов-потомков, которые располагаются ниже по дереву (по соглашению, деревья 'растут' вниз, а не вверх, как это происходит с настоящими деревьями). Узел, имеющий потомка, называется узломродителем относительно своего потомка (или узлом-предшественником, или старшим). Каждый узел имеет не больше одного предка. Высота узла

— это максимальная длина нисходящего пути от этого узла к самому нижнему узлу (краевому узлу), называемому листом. Высота корневого узла равна высоте всего дерева. Глубина вложенности узла равна длине пути до корневого узла.

Упорядоченные деревья являются наиболее распространѐнными среди древовидных структур. Двоичное дерево поиска —

одно из разновидностей упорядоченного дерева. Это пример неупорядоченного дерева.

Двоичное дерево поиска (binary search tree, BST) —

это двоичное дерево, для которого выполняются следующие дополнительные условия (свойства дерева поиска):

Оба поддерева - левое и правое, являются двоичными деревьями поиска.

У всех узлов левого поддерева произвольного узла X значения ключей данных меньше, нежели значение ключа данных узла X.

У всех узлов правого поддерева произвольного узла X значения ключей данных не меньше, нежели значение ключа данных узла X.

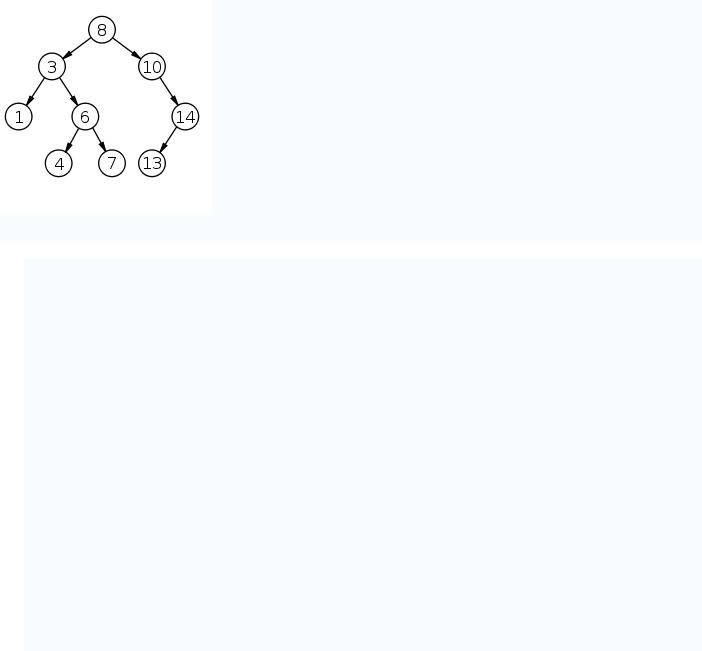
Очевидно, данные в каждом узле должны обладать ключами, на которых определена операция сравнения меньше.

Как правило, информация, представляющая каждый узел, является записью, а не единственным полем данных. Однако это касается реализации, а не природы двоичного дерева поиска.

Для целей реализации двоичное дерево поиска

можно определить так:

Двоичное дерево состоит из узлов (вершин) — записей вида (data, left, right), где data — некоторые данные привязанные к узлу, left и

right — ссылки на узлы, являющиеся детьми данного узла - левый и правый сыновья соответственно. Для оптимизации алгоритмов конкретные реализации предполагают также, определения в каждом узле кроме корневого поля parent - ссылки на родительский элемент.

Данные (data) обладают ключом (key) на котором определена операция сравнения "меньше". В конкретных реализациях это может быть пара (key, value) - (ключ и значение), или ссылка на такую пару, или простое определение операции сравнения на необходимой структуре данных или ссылке на неѐ.

Для любого узла X выполняются свойства дерева поиска:

key[left[X]] < key[X] ≤ key[right[X]], т. е. ключи данных

родительского узла больше ключей данных левого сына и нестрого меньше ключей данных правого.

Базовый интерфейс двоичного дерева поиска состоит из трех операций:

FIND(K) — поиск узла, в котором хранится пара (key, value) с key = K.

INSERT(K,V) — добавление в дерево пары (key, value) = (K, V).

REMOVE(K) — удаление узла, в котором хранится пара (key, value) с key = K.

По сути, двоичное дерево поиска — это структура данных, способная хранить таблицу пар (key, value) и поддерживающая три операции: FIND,

INSERT, REMOVE.

Поиск элемента (FIND)

Если дерево пусто, сообщить, что узел не найден, и остановиться.

Иначе сравнить K со значением ключа корневого узла X. o Если K=X, выдать ссылку на этот узел и остановиться.

o Если K>X, рекурсивно искать ключ K в правом поддереве Т. o Если K<X, рекурсивно искать ключ K в левом поддереве Т.

Добавление элемента (INSERT)

Если дерево пусто, заменить его на дерево с одним корневым узлом

((K,V), null, null) и остановиться.

Иначе сравнить K с ключом корневого узла X.

oЕсли K>=X, рекурсивно добавить (K,V) в правое поддерево Т. oЕсли K<X, рекурсивно добавить (K,V) в левое поддерево Т.

Удаление узла (REMOVE)

Если дерево T пусто, остановиться

Иначе сравнить K с ключом X корневого узла n.

o Если K>X, рекурсивно удалить K из правого поддерева Т. o Если K<X, рекурсивно удалить K из левого поддерева Т. o Если K=X, то необходимо рассмотреть три случая.

oЕсли обоих детей нет, то удаляем текущий узел и обнуляем ссылку на него у родительского узла.

o Если одного из детей нет, то значения полей второго ребѐнка m ставим вместо соответствующих значений корневого узла, затирая его старые значения, и освобождаем память, занимаемую узлом n.

o Если оба ребѐнка присутствуют, то

найдѐм узел m, являющийся самым левым узлом правого поддерева;

присвоим ссылке Left(m) значение Left(n)

ссылку на узел n в узле Parent(n) заменить на Right(n);

освободим память, занимаемую узлом n (на него теперь никто не указывает).

Множества на основе бинарных деревьев

Множества более эффективно можно реализовать с помощью упорядоченных бинарных деревьев.

К сожалению, если мы составляем произвольное упорядоченное бинарное дерево, оно может быть разной структуры. То есть, множество из одних и тех же элементов может представляться разными деревьями.

Если дерево будет близко по высоте к сбалансированному, то вычислительная сложность базовых алгоритмов равна О(log n), поскольку она определяется как раз высотой дерева. Деревья мы можем представлять при помощи списков. Каждая вершина будет списком из трех элементов: информация о вершине (ее обычно называют входом вершины), левое поддерево и правое поддерево. В случае пустых списков на месте левого и правого поддерева будет означать, что этот элемент – лист дерева.

Мы можем описать это представление при помощи следующих процедур:

(define (entry tree) (car tree)) (define (left-branch tree) (cadr tree))

(define (right-branch tree) (caddr tree)) (define (make-tree entry left right)

(list entry left right))

Теперь можно написать процедуру element-of-set? с использованием вышеописанной стратегии:

(define (element-of-set? x set) (cond ((null? set) false) ((= x (entry set)) true) ((< x (entry set))

(element-of-set? x (left-branch set))) ((> x (entry set))

(element-of-set? x (right-branch set)))))

Добавление элемента к множеству реализуется похожим образом и также требует О(log n) шагов. Чтобы добавить объект x, мы сравниваем его с содержимым вершины и определяем, должны ли мы добавить x к левой или правой ветви, а добавив x к соответствующей ветви, мы соединяем результат с изначальным входом и второй ветвью.

Если x равен входу, мы просто возвращаем вершину. Если нам требуется добавить x к пустому дереву, мы порождаем дерево, которое содержит x на входе и пустые левое и правое поддеревья. Вот процедура:

(define (adjoin-set x set)

(cond ((null? set) (make-tree x ’() ’())) ((= x (entry set)) set)

((< x (entry set)) (make-tree (entry set)

(adjoin-set x (left-branch set)) (right-branch set)))

((> x (entry set)) (make-tree (entry set)

(left-branch set)

(adjoin-set x (right-branch set))))))

Рассматривая вопрос совместимости разных типов данных, напишем функции, которые обеспечивают преобразование произвольного бинарного дерева в список. Причем, если дерево упорядоченное, то и список получится упорядоченный. Обратное преобразование превращает упорядоченный список в сбалансированное бинарное дерево.

(define (tree->list-1 tree) (if (null? tree) ’()

(append (tree->list-1 (left-branch tree)) (cons (entry tree)

(tree->list-1 (right-branch tree))))))

(define (tree->list-2 tree)

(define (copy-to-list tree result-list) (if (null? tree) result-list

(copy-to-list (left-branch tree) (cons (entry tree)

(copy-to-list (right-branch tree) result-list)))))

(copy-to-list tree ’()))

Следующая процедура list->tree преобразует упорядоченный список в сбалансированное бинарное дерево. Вспомогательная процедура partialtree принимает в качестве аргументов целое число n и список, по крайней мере, из n элементов, и строит сбалансированное дерево из первых n элементов дерева. Результат, который возвращает , — это пара (построенная через cons), car которой есть построенное дерево, а cdr — список элементов, не включенных в дерево.

(define (list->tree elements)

(car (partial-tree elements (length elements))))

(define (partial-tree elts n) (if (= n 0) (cons ’() elts)

(let ((left-size (quotient (- n 1) 2)))

(let ((left-result (partial-tree elts left-size))) (let ((left-tree (car left-result))

(non-left-elts (cdr left-result)) (right-size (- n (+ left-size 1)))) (let ((this-entry (car non-left-elts))

(right-result (partial-tree (cdr non-left-elts) right-size)))

(let ((right-tree (car right-result)) (remaining-elts (cdr right-result)))

(cons (make-tree this-entry left-tree right-tree) remaining-elts))))))))

В теории существует несколько методик самобалансирования деревьев при изменении, но наиболее популярными являются только две из них: красно-черные деревья и AVL-деревья. По большому счету, разница у них несущественная: первые несколько быстрее на вставке/удалении, вторые – на поиске. АВЛ-деревья названы по первым буквам фамилий их изобретателей, Г. М. Адельсона-Вельского и Е. М. Ландиса, которые впервые предложили использовать АВЛ-деревья в 1962.