контрольная работа № 2

Решать такие задачи легче всего, применяя законы Кирхгофа.

Первый закон Кирхгофа: алгебраическая сумма токов в узле равна нулю,

n

Ii 0 .

i 1

Узлом в цепи называют точку соединения трех и более проводников.

Токи, входящие в узел, считают положительными. Токи, выходящие из узла, считают отрицательными.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на всех участках замкнутой цепи равна алгебраической сумме ЭДС в этой же цепи,

При применении второго закона Кирхгофа необходимо учитывать знаки слагаемых в левой и правой частях уравнения. Падение напряжения на сопротивлении IR записывается в уравнении со знаком « + », если направление обхода на этом участке цепи совпадает с направлением тока на этом участке,

и наоборот, если направление обхода на этом участке цепи не совпадает с направлением тока, то произведение IR записывается со знаком « ». ЭДС источника тока считают положительным и записывают со знаком « + », если направление обхода совпадает с направлением поля сторонних сил,

действующих внутри источника. Сторонние силы разделяют заряды, и за направление этих сил принимают силы,

действующие на положительные заряды. На рисунке стрелкой показано направление поля сторонних сил внутри источника тока.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Порядок решения задач на законы Кирхгофа

1. Нарисовать схему цепи. На рисунке выбрать и показать направления токов на всех участках цепи, при этом надо учесть, что в узел токи не могут

21

только входить или только выходить из узла. Это следует из первого закона

Кирхгофа.

2.Выбрать замкнутые контуры обхода для применения второго закона Кирхгофа. Показать на рисунке направление обхода по контуру. Контуров может быть несколько. Число независимых уравнений, которые можно составить по второму закону Кирхгофа, меньше, чем число контуров. Для того чтобы составить необходимое число независимых уравнений, надо придерживаться следующего правила: выбирать контуры так, чтобы в каждый новый контур входил хотя бы один участок цепи, которого бы не было ни в одном из ранее рассмотренных контуров.

3.Используя первый закон Кирхгофа, можно написать (n – 1) уравнений,

где n число узлов в рассматриваемой цепи.

4. Воспользоваться вторым законом Кирхгофа и записать такое число уравнений, чтобы число уравнений, составленных по первому и второму законам Кирхгофа, равнялось числу неизвестных величин в задаче. При этом надо учитывать следующее правило знаков: падение напряжения на каждом участке записывается со знаком «+», если направление обхода по этому участку совпадает с направлением тока на нем. И наоборот, если обход совершался по этому сопротивлению обратно направлению тока, то ставится знак « ».

ЭДС записывается со знаком «+» в том случае, когда направление обхода совпадает с направлением поля сторонних сил в источнике тока и наоборот.

Поле сторонних сил внутри источника всегда направлено от отрицательного полюса к положительному.

5. Решить полученную систему уравнений и найти искомые величины. В

результате решения полученной системы уравнений определяемые величины могут получаться отрицательными. Отрицательное значение тока указывает на то, что фактическое направление тока на данном участке цепи обратно тому,

которое мы выбрали.

22

П р и м е р 1. 7

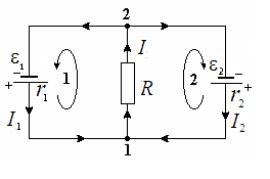
Два элемента с одинаковыми ЭДС 1 = 2 = 2В и внутренними сопротивлениями r1 = 1 Ом, r2 = 2 Ом замкнуты на внешнее сопротивление R.

Через первый элемент течет ток I1 = 1 А. Найдите сопротивление R, ток I2, теку-

щий через второй элемент, и ток I, текущий через сопротивление R. Схема

соединения показана на рисунке.

3. Составим уравнение, используя первый закон Кирхгофа. Узлов два,

поэтому можно составить только одно уравнение, например для первого узла:

I1 + I2 I = 0.

Токи, входящие в узел, пишем со знаком « + », а выходящие со знаком « – ».

Уравнение для второго узла будет тождественно первому.

4. Применим второй закон Кирхгофа для первого контура обхода.

Падение напряжения на всех участках этого контура пишем со знаком «+», так как направление обхода на всех участках совпадает с направлением тока на этих участках.

U = IR +I1 r.

23

В этот контур входит только один источник тока 1, и направление обхода по контуру совпадает с направлением поля сторонних сил, так как силы этого поля направлены от отрицательного полюса к положительному, т.е. вниз.

Запишем уравнение

IR + I1r1 = 1.

Для второго контура, рассуждая аналогично, получим U2 = I2r2 + IR. ЭДС будет входить в уравнение также со знаком «+».

Второе уравнение имеет вид I2R2 + IR = 2.

5. Получили систему из трех уравнений с тремя неизвестными.

I1 I2 I;

IR I1r1 1;IR I2r2 2.

Решая систему, находим величину тока I2.

I2 I1r1 1 2 0,5A . r2

Полный ток через сопротивление R равен сумме токов

I = I1 + I2 = 1,5 A.

Сопротивление R находим из одного из уравнений системы:

R 23 Ом 0,66Ом .

Ответ. Ток через второй источник равен I2 = 0,5 А, суммарный ток I = I1 + I2 = =1,5 А. Внешнее сопротивление R = 0,66 Ом.

П р и м е р 1. 8

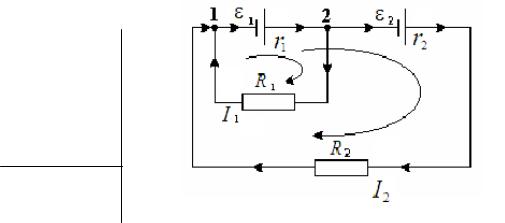
Два одинаковых элемента имеют ЭДС 1 = 2 = 2 В и внутренние сопротивления r1 = r 2 = 0,5 Ом. Найдите токи I1 и I2, текущие через сопротивления R1 = 0,5 Ом и R2 = 1,5 Ом, а также ток I через первый элемент.

Схема заданной цепи изображена на рисунке.

24

Дано:

1 = 2 = 2 В r1 =r2=0,5 Ом

R1 = 0,5 Ом

R2 = 1,5 Ом

Найти:

I1 – ? I2 – ?

I – ?

Решение:

1. Выберем направления токов на всех участках так, как показано на рисунке. Видим, что в узлах 1 и 2 есть входящие и есть выходящие токи,

значит, направления токов выбраны верно.

2.Выберем два контура обхода: большой и малый. Укажем направления обходов по контурам. Контуров обхода в заданной цепи можно выбрать три, но для нахождения трех неизвестных величин достаточно трех уравнений. Узлов всего два, поэтому можно составить только одно уравнение, применяя первый закон Кирхгофа. Недостающих два уравнения составим, используя второй закон Кирхгофа.

3.Для первого узла запишем:

I2 + I1 – I = 0.

4. Учитывая правила определения знаков всех слагаемых при применении второго закона Кирхгофа, для большого контура получаем уравнение

I r1 + I2r2 + I2R2 = 1 + 2,

для малого контура уравнение

Ir1 + I1R1 = 1.

5.Получили систему из трех уравнений с тремя неизвестными

величинами I1, I2 и I.

25

I2 I1 I;

Ir1 I2r2 I2 R2 1 2 ;Ir1 I1R1 1.

Решать систему линейных уравнений можно разными способами. В

случае, когда система состоит из большого числа уравнений, удобно пользоваться методом Крамера (методом определителей). Проиллюстрируем применение этого метода решения на нашей системе уравнений. Для этого

Если поделить правую и левую части второго и третьего уравнении на 0,5,

I1 I2 I 0;

получим 0 4I2 I 8;

I1 0 I 4.

Искомые величины токов по методу определителей находятся следующим

– определители, которые получаются заменой соответствующих столбцов определителя столбцами, полученными из свободных членов уравнений,

образующих систему (с учетом заданных числовых значений). Запишем эти определители:

26

Значение третьего тока можно найти аналогичным способом, но проще его значение получить из первого уравнения нашей системы:

I2 + I1 – I = 0, или I = I2 + I1 = 1,33 + 1,33 = 2,66 А.

Знаки у всех полученных значений силы тока положительные, это свидетельствует о том, что при произвольном выборе направлений токов,

указанных на рисунке, все направления токов были выбраны правильно.

Ответ. I1 = 1,33 А ; I2 = 1,33 А ; I = I1 + I2 = 2,66 А.

2.ЭЛЕКТРОМАГНЕТИЗМ

2.1.Магнитное поле постоянного тока

Связь магнитной индукции B с напряженностью H магнитного поля выражается формулой

B 0 H ,

где – относительная магнитная проницаемость среды;

0 4 10 7 Гн/м – магнитная проницаемость вакуума (магнитная постоянная).

Для вакуума и воздуха 1, и тогда

B0 0 H.

Закон Био-Савара-Лапласа:

где d B – индукция магнитного поля, создаваемого элементом тока Idl ; r –

радиус-вектор, проведенный от элемента тока в рассматриваемую точку пространства; – угол между векторами Idl и r .

Теорема о циркуляции вектора индукции магнитного поля

27

где в правой части теоремы стоит алгебраическая сумма токов, охватываемых контуром интегрирования.

Величина вектора магнитной индукции в центре кругового тока

B 0 I , 2R

где R – радиус кругового витка.

Величина магнитной индукции на оси кругового тока на расстоянии h от цента витка до точки, в которой определяется магнитная индукция:

Магнитная индукция поля, создаваемого отрезком прямолинейного проводника,

B 0 I cos 1 cos 2 , 4 r0

где r0 – длина перпендикуляра, опущенного из рассматриваемой

точки на проводник или его продолжение; 1, 2 – углы между первым и последним элементами тока и радиус-векторами, проведенными от них в рассматриваемую точку.

Для бесконечно длинного проводника с током

Индукция магнитного поля бесконечно длинного соленоида

B 0nI ,

где n = N/l – число витков, приходящихся на единицу длины соленоида. Эта формула верна и для тороида с равномерной намоткой плотно прилегающих друг к другу N витков.

28

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

П р и м е р 2. 1

Бесконечно длинный прямой проводник, по

которому течет ток I = 5,0 А, согнут под прямым углом так, как показано на рисунке. Найти индукцию

магнитного поля в точке А, лежащей на биссектрисе прямого угла на расстоянии d = 10 см от вершины угла.

Анализ:

Весь проводник можно разделить на три участка: участок конечной длины ОС и два полубесконечных прямолинейных проводника 1 и 3. По

BA B1A B2 A B3 A .

Для нахождения величин индукций магнитного поля, создаваемого участками 1, 2 и 3 проводника, необходимо применить формулу вычисления модуля вектора В поля, создаваемого отрезком прямолинейного проводника:

B 0 I cos 1 cos 2 .

Для определения направлений векторов магнитной индукции в разных

случаях надо воспользоваться правилом правого винта и нарисовать силовые линии поля, проходящие через интересующие нас точки.

Решение:

Силовые линии, проходящие через точку А, – это окружности радиуса r,

лежащие в плоскостях, перпендикулярных к проводникам 1 и 2. Векторы B1A и

B2 A направлены по касательным к этим линиям в точке А. Вектор B1A

направлен в точке А перпендикулярно к плоскости чертежа, к нам. Также будет направлен и вектор B2 A . Следовательно, для модуля вектора BA можно записать

ВА = В1А + В2А .

29

Модуль вектора B1 найдем, воспользовавшись формулой

B1 μμ4π0rI cos 1 cos 2 .

На рисунке показаны 1, 2 – углы между первым и последним элементами тока и радиус-

векторами, проведенными от них в рассматриваемую точку.

В данном случае 1 0 (проводник бесконечно длинный), 2 = 1350,

так как для этого участка проводника с током углы 1 = 45 и 2 = 90; это видно на рисунке, где эти углы отмечены штрихами.

Для третьего участка проводника с током все углы между радиус-

вектором и любым элементом тока будут равны нулю, поэтому получим

Таким образом, индукция магнитного поля в точке А равна:

30