контрольная работа № 3

Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу

найденные точки и получим траекторию точки, совершающей колебания в соответствии с уравнениями движения, заданными по условию.

Для того чтобы указать направление движения точки, последим за тем,

как изменяется ее положение с течением времени.

В начальный момент t = 0 координаты точки равны

х(0) = 1 см и у (0) = 2 см.

В последующий момент времени, например при t = Т/4, координаты точек изменятся и станут равными

х(Т/4) = 1 · cos ( Т4 ) = 1 · cos ( 2Т Т4 ) = 1 · cos ( 2 ) = 0 см,

у(Т/4) = 2 · cos ( Т4 ) = 1 · cos ( 2Т Т4 ) = 1 · cos ( 2 ) = 0 см .

При t = Т/2 координаты будут равны

х(Т/2) = 1· cos ( Т2 ) = 1 · cos ( 2Т Т2 ) =

= 1 · cos( π) = –1 см,

у(Т/2) = 2 · cos ( Т2 ) = 2 · cos ( 2Т Т2 ) = = 2 · cos( π) = –2 см.

Зная положения точек в начальный и последующий моменты времени, можно указать направление движения точки по

траектории. На рисунке эти направления указаны стрелками.

П р и м е р 3.4

Амплитуда затухающих колебаний математического маятника за время t1 = 1 мин уменьшилась в два раза. Во сколько раз уменьшится амплитуда за время t2 = 3 мин?

21

A(t)

Определить: A(t t2 ) = ? Решение:

Амплитуда затухающих колебаний уменьшается с течением времени по следующему закону:

А (t) = А0 е-βt ,

где А(t) – амплитуда колебаний в момент времени t; А0 – амплитуда колебаний в начальный момент времени t = 0; β – коэффициент затухания. Тогда

Прологарифмировав это уравнение, получаем ln е t1 = βt1 = ln 2 ,

отсюда выразим коэффициент затухания β :

β = ln 2 . t1

Запишем искомое отношение:

Подставим выражение для коэффициента β в показатель экспоненты и получаем

22

П р и м е р 3.5

Гиря массой m = 0,50 кг подвешена к пружине, жесткость которой

k = 32,0 Н/м, и совершает затухающие колебания. Определить их период Т в

Решение:

Сопротивление среды уменьшает частоту свободных колебаний и,

соответственно, увеличивает период колебаний. Период затухающих колебаний определяется по соотношению

соотношению

ω0 = mk .

Коэффициент затухания равен

β = Т ,

где λ – логарифмический декремент затухания. Для того чтобы найти величину

λ, обратимся к уравнению затухающих колебаний

х = А0 е-βt ∙cos (ω t + φ ) .

Уменьшающуюся со временем амплитуду выразим так:

23

Пользуясь введенными в условие задачи обозначениями, можно записать следующее:

Отсюда, логарифмируя, определяем λ:

λ = ln N . n

Подставив численные значения N и n для двух случаев, получим

Теперь запишем формулу для периода колебаний Т с учетом выражения

для β:

Получилось квадратное уравнение относительно Т. Решая его, находим

(отбросив отрицательный корень)

λ12 << 4π2, поэтому, сохраняя достаточную точность вычислений, можно пренебречь слагаемым λ1 2, тогда

2 Т1 = 0 .

Во втором случае величину λ2 2 отбросить нельзя. Производим вычисления:

24

Ответ: Т1 =0,78 с, Т2 = 0,81 с.

П р и м е р 3.6

Колебательный контур состоит из конденсатора емкостью С = 0,25 мкФ и катушки индуктивностью L =1,015 Гн. Омическим сопротивлением цепи пренебречь. В начальный момент времени заряд на обкладках конденсатора максимален и равен q0 = 2,5∙10-6 Кл. Написать для данного контура уравнения

(с числовыми коэффициентами) изменения разности потенциалов на обкладках конденсатора и силы тока в цепи от времени. Найти значения разности потенциалов на обкладках конденсатора и силы тока в цепи в моменты времени t1 = T/4 и t2 = T/2.

Дано: С = 0,025∙10-6 Ф, L = 1,015 Гн, R = 0, q0 =2,5∙1-10-6 Кл.

Определить: u(t) =? i(t) =?

Решение:

Уравнение изменения заряда на обкладках конденсатора со временем имеет вид

q = q0 ∙ cos (ω0t + φ ).

Начальная фаза колебаний равна нулю, следовательно, q = q0 ∙ cos ω0t .

Изменение напряжения на обкладках конденсатора задается уравнением u(t) = Cq qC0 cos 0t U0 cos 0t ,

где ω0 – циклическая частота собственных колебаний в контуре,

0 2Т ,

25

где Т – период собственных колебаний:

Для того чтобы записать с числовыми коэффициентами уравнение изменения разности потенциалов, произведем вычисления:

Таким образом, получаем уравнение в виде

U(t) = 100 · cos 2000πt, В .

Изменение силы тока со временем задается уравнением

Определить: 1) длину волны λ ; 2) фазу φ колебаний , смещение ξ, скорость ξ′

и ускорение ξ′′ точки, отстоящей на расстоянии l = 45 м от источника волн в

1.Длина волны равна расстоянию, на которое фронт волны перемешается за один период, поэтому

λ= T , λ = 15∙ 1,2 = 18 м.

2.Запишем уравнение волны

Подставляя в уравнение (1) найденное значение фазы, находим величину смещения частицы в заданный момент времени:

ξ = 2 ∙ сos 53 = 0,01 м.

Скорость и ускорение точки находим, взяв соответственно первую и вторую производные смещения по времени.

Скорость:

ξ′ = – ωА sin ω ( t – l / ),

27

ξ′ = – 2 ∙ 1,2 2 sin 53 = 9 ∙ 10-2 м/с .

Ускорение:

ξ′′ = – ω2 А cos ω ( t – l / ),

3. Разность фаз ∆φ колебаний двух точек волны связана с расстоянием ∆х

между этими точками соотношением

П р и м е р 3.8

На стеклянный клин (абсолютный показатель преломления стекла n = 1,5)

нормально к его грани падает монохроматический свет с длиной волны

λ = 0,6 мкм. В возникающей при этом интерференционной картине на отрезке длиной а = 1 см наблюдается N = 10 полос. Определить преломляющий угол φ клина.

Дано: λ = 6 ∙10-7м, а =1 ∙ 10-2 м, N = 10, n = 1,5.

Определить: φ =?

Решение:

Параллельный пучок света, падая нормально к грани клина, отражается как от верхней, так и от нижней

грани. Эти пучки когерентны, и поэтому наблюдается устойчивая картина интерференции. Так как интерференционные полосы наблюдаются при малых углах клина, то отраженные лучи 1 и 2 (см. рисунок) практически параллельны.

Темные полосы видны на тех участках клина, для которых оптическая разность хода кратна нечетному числу половины длины волны:

∆ = ( 2m + 1 ) 2 ,

где m = 0,1,2 . . .

Для лучей 1 и 2 оптическая разность хода

∆ = 2 dm n + 2 ,

где n – показатель преломления стекла, по условию равный 1,5, а слагаемое

λ/2 обусловлено изменением фазы луча 1 при отражении от оптически более плотной среды. Приравнивая правые части этих выражений, получаем

Искомый угол φ равен (см. рисунок на с. 28)

φ = dm N dm ,

a

так как из-за малости угла φ ≈ sin φ.

Отсюда

В соответствии с общим правилом перевода из радиан в градусы

П р и м е р 3.9

Между стеклянной пластинкой и лежащей на ней плосковыпуклой стеклянной линзой налита жидкость, показатель преломления которой меньше

показателя преломления стекла. Радиус r8 восьмого темного кольца Ньютона при наблюдении в отраженном свете (λ = 700 нм) равен 2 мм. Радиус кривизны

Решение:

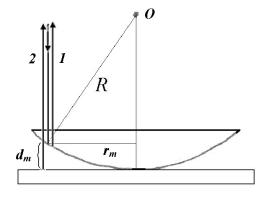
В отраженном свете кольца Ньютона образуются при наложении лучей,

отраженных от нижней поверхности линзы и верхней поверхности плоскопараллельной пластины. Так как радиус кривизны линзы велик, то лучи

1 и 2 (см. рисунок) практически параллельны.

30