
Методичка по инженерке
.pdf
Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
||
Морозова Н.Н., Зигулев А.Г. |
|||
|
|
||
Относительное положение прямой и плоскости |
|||
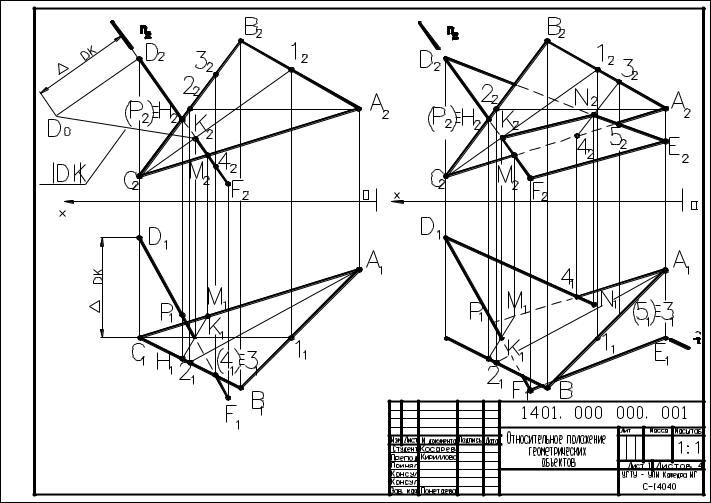
Задание 1.1. Определить расстояние от точки D |
|
||
до плоскости треугольника ABC (рис. 1). |
|
||
Прямая перпендикулярна плоскости, если она перпендикулярна |
|||
двум пересекающимся прямым, принадлежащим этой плоскости. |
|||
В качестве пересекающихся прямых выбираем горизонталь и фрон- |
|||
таль плоскости, так как при прямоугольном проецировании прямой |
|||
угол проецируется без искажения, если одна его сторона параллельна |
|||
плоскости проекций, а другая не перпендикулярна ей. |
|
||
Алгоритм решения задачи: |
|
|
|
1. Из точки D проводим перпендикуляр DF произвольной дли- |
|||
ны, используя горизонталь А2 и фронталь С1 плоскости треугольника |
|||
ABC. При этом горизонтальная проекция перпендикуляра D1F1 пер- |
|||
пендикулярна горизонтальной проекции горизонтали A121, а фрон- |
|||
тальная проекция перпендикуляра D2F2 перпендикулярна фронталь- |
|||
ной проекции фронтали C212. (D1F1 A121; D2F2 C212). |
|
||
2. Определим точку пересечения построенного перпендикуляра |
|||
DF с плоскостью треугольника АВС. Для этого перпендикуляр DF за- |
|||
ключаем во вспомогательную фронтально проецирующую плоскость |
|||
α. Находим линию пересечения плоскости треугольника АВС и вспо- |
|||
могательной плоскости α – прямую MН. Определим точку К, точку |
|||
пересечения прямой MН с перпендикуляром DF; это и есть искомая |
|||
точка пересечения перпендикуляра DF с плоскостью треугольника |
|||
ABC. |
|
|
|
3. Определим натуральную величину отрезка DК (расстояния |
|||
от точки D до плоскости треугольника АВС) способом прямоугольно- |
|||
го треугольника. Прямоугольный треугольник строим на фронтальной |
|||
плоскости проекций. В качестве одного катета выбираем проекцию |
|||
перпендикуляра D2K2, вторым катетом будет отрезок ∆YDK, равный |
|||
разности координат Y точек D и K. |
|
||
4. Видимость проекций перпендикуляра DK определим, ис- |
|||
пользуя конкурирующие точки. Точка пересечения всегда видима и |
|||
является границей видимости. |
|
|
|
ГОУ ВПО «УГТУ-УПИ» – 2005 |
|
Стр. 21 из 33 |
|

Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
На фронтальной плоскости проекций в качестве конкурирующих точек рассмотрим точки Р и Н, принадлежащие разным геометрическим объектам. Точка Р принадлежит перпендикуляру DK, а точка Н стороне треугольника СВ. Координата Y точки Н больше координаты Y точки P, следовательно, точка H расположена от фронтальной плоскости проекций дальше, чем точка Р. На фронтальной плоскости проекций сторона треугольника CB видима, DK невидима. На горизонтальной плоскости проекций в качестве конкурирующих точек выбираем точки 3 и 4, принадлежащие разным геометрическим объектам. Точка 4 принадлежит прямой DK, а точка 3 принадлежит стороне треугольника СВ. Координата Z точки 3 больше координаты Z точки 4, следовательно, точка 3 расположена выше точки 4. На горизонтальной плоскости проекций сторона треугольника CB видима, прямая DK невидима.
Относительное положение плоскостей
Задание 1.2. Построить плоскость DEF, перпендикулярную треугольнику ABC (рис. 1).
Две плоскости взаимно перпендикулярны, если одна из них содержит прямую, перпендикулярную другой плоскости. Искомая плоскость должна содержать в себе заданную прямую DE и перпендикуляр, опущенный из любой точки этой прямой на заданную плоскость треугольника АВС. (Например, из точки D – перпендикуляр DF).
Алгоритм решения задачи:
1.Строим плоскость, перпендикулярную плоскости треугольника АВС, используя исходную прямую DE и построенный в предыдущей задаче перпендикуляр DF.
2.Две плоскости пересекаются по прямой линии. Для построения линии пересечения необходимо найти две точки, одновременно принадлежащие двум плоскостям. Точка К принадлежит треугольнику ABC и треугольнику DEF. Вторую точку N определяем, используя алгоритм нахождения точки пересечения прямой DE с плоскостью ABC, как в задании 1. Линия пересечения плоскостей всегда видима.
3.Определим видимость пересекающихся плоскостей. Видимость плоскостей определяется с помощью конкурирующих точек. Видимость стороны DF определена в задании 1.1. Зная видимость стороны DF, можно определить видимость остальных сторон треугольников.
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 22 из 33 |

Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
ОТНОСИТЕЛЬНОЕ ПОЛОЖЕНИЕ ПОВЕРХНОСТИ И ПЛОСКОСТИ
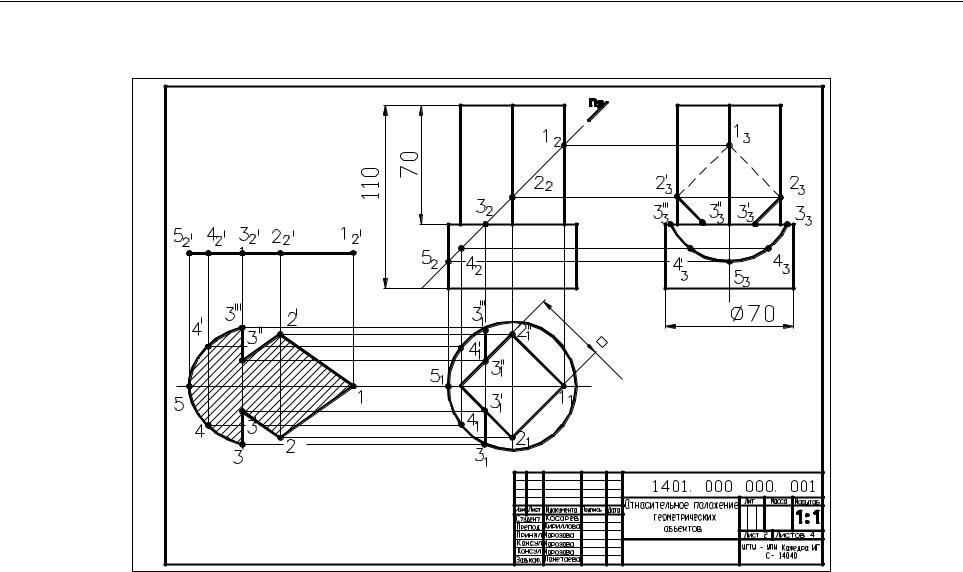
Задание 2.1. Построить проекции сечения комбинированной поверхности плоскостью α (рис. 2).
Плоскость пересекает поверхность по линии, все точки которой одновременно принадлежат поверхности и плоскости.
Эта линия называется линией сечения поверхности плоскостью.
При построении проекций точек линии сечения используют способ вспомогательных секущих плоскостей:
проводят вспомогательные плоскости-посредники, которые пересекают поверхность по простым сечениям (окружность, прямоугольник, треугольник); строят несколько сечений;
искомые точки, принадлежащие поверхности и заданной плоскости α, определяющие контур сечения, находятся на пересечении заданной плоскости α и плоскости-посредника.
Алгоритм решения задачи:
1. Заданная плоскость α является фронтально проецирующей,
поэтому фронтальная проекция сечения (12 – 52) поверхности совпадает с фронтальным следом плоскости α.
Построим горизонтальную и профильную проекции сечения.
2.Точки пересечения фронтального следа плоскости и очерков поверхностей определяют характерные точки сечения 12; 32; 52.
Сечение призмы заданной плоскостью α – пятиугольник. Определим характерные точки сечения – точки пересечения плоскости α с ребрами призмы (т. 1, 2) и точку, лежащую в основании призмы (т.3). Промежуточные точки для построения пятиугольника не нужны.
3. Плоскость α рассекает цилиндр по эллипсу. Фронтальная проекция эллипса (отрезок 32 – 52) принадлежит фронтальному следу плоскости. Горизонтальная проекция точек сечения совпадает с горизонтальной проекцией цилиндра. Профильную проекцию эллипса строим в проекционной связи по горизонтальной и фронтальной проекциям.
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 23 из 33 |

Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
Задание 2.2 Построить натуральную величину сечения поверхности плоскостью (рис.2).
Натуральную величину сечения строим способом плоскопараллельного перемещения. При этом способе все точки сечения перемещаются в плоскостях, параллельных плоскости проекций, без изменения вида и размеров геометрического объекта. Геометрический объект – сечение поверхности перемещается из общего положения в частное.
Плоскость α преобразуем в горизонтальную плоскость уровня. При этом фронтальная проекция сечения поверхностей располагается параллельно оси OX и не изменяется по величине. Координаты Y точек, принадлежащих сечению, не меняются, т. к. точки перемещаются в плоскостях, параллельных фронтальной плоскости проекций.
Относительное положение поверхностей
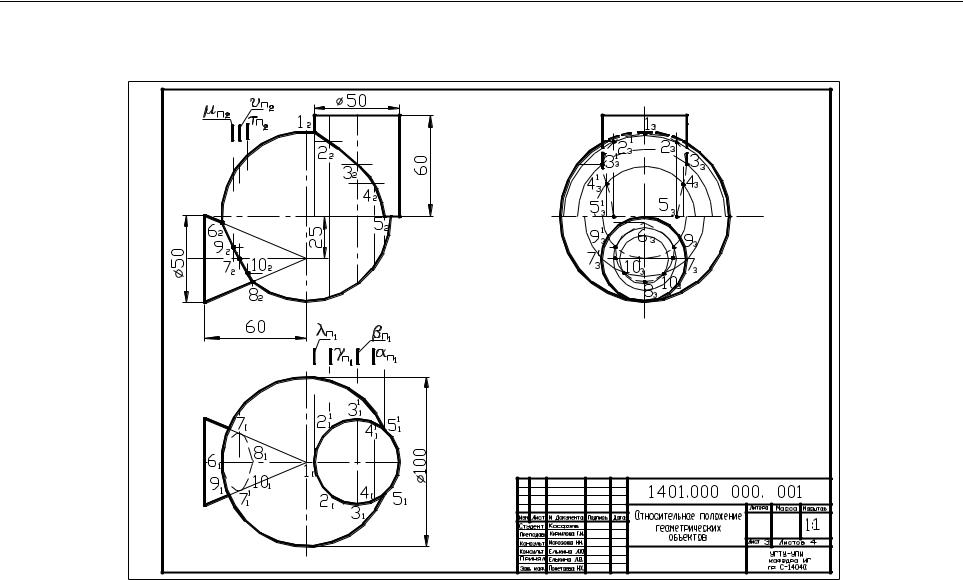
Задание 3.1. Построить линии пересечения заданных поверхностей способом секущих плоскостей (рис. 3).
1.Заданная фигура состоит из сферы, цилиндра прямого кругового и конуса прямого кругового.
2.Цилиндр – поверхность вращения с прямолинейной образующей. Ось вращения цилиндра перпендикулярна горизонтальной
плоскости проекций П1, все его образующие являются горизонтально проецирующими прямыми, поэтому линия пересечения цилиндра со сферой на горизонтальной плоскости проекций совпадает очерком цилиндра.
Конус – поверхность вращения с прямолинейной образующей, которая пересекает ось вращения в постоянной точке S. Ось вращения конуса перпендикулярна профильной плоскости проекций.
Сфера – нелинейчатая поверхность вращения, образующей является окружность.
3.Линия пересечения цилиндра и сферы – пространственная кривая четвертого порядка. Характерными точками линии пересечения цилиндра и сферы, являются:
точки пересечения очерков поверхностей 5;
крайняя левая точка очерка цилиндра 1; самая ближняя 3 и самая удаленная 31 точки линии пересечения по отношению к наблюдателю.
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 24 из 33 |

Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
Для построения линии пересечения сферы и цилиндра проводим вспомогательные профильные секущие плоскости α, β, γ, λ, которые пересекают цилиндр по прямоугольникам, а сферу по окружности. Прямоугольник и окружность проецируются в натуральную величину на профильную плоскость проекций и пересекаются в точках (1, 2, 3, 4, 5 и т.д.), принадлежащих линии пересечения сферы и цилиндра.
4.Фронтальную проекцию линии пересечения цилиндра и сферы строим в проекционной связи по горизонтальной и профильной проекциям.
5.На фронтальной плоскости проекций линия пересечения видима, на профильной плоскости проекций не видима.
6.Линия пересечения конуса и сферы пространственная кривая четвертого порядка. Характерными точками линии пересечения сферы и конуса являются точки пересечения очерков поверхностей на фронтальной плоскости проекций: точки 6 и 8.
7.Для построения промежуточных точек 7, 9, 10 проводим вспомогательные профильные секущие плоскости µ, υ, τ, которые пересекают сферу и конус по окружностям. Радиусы окружностей – расстояние от оси вращения поверхности до очерка поверхности. Сечения (окружности) проецируются в натуральную величину на профильную плоскость проекций. Точки пересечения окружностей – искомые точки линии пересечения поверхностей. Для построения фронтальных проекций точек 7, 9, 10 проводим горизонтальные линии связи до фронтальных проекции секущих плоскостей µп2, υп2, τп2.
8.Горизонтальную проекцию линии пересечения конуса и сферы строим в проекционной связи по фронтальной и профильной проекциям.
9.На фронтальной плоскости проекций линия пересечения видима. На профильной и горизонтальной плоскостях проекций линия невидима.
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 25 из 33 |

Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
Относительное положение поверхностей Построение развертки поверхности
Задание 4.1. Построить линию пересечения поверхностей способом вспомогательных концентрических сфер (рис.4).
1.В условии задачи заданы поверхности: самопересекающийся тор с профильно-проецирующей осью вращения и конус круговой наклонный усеченный.
2.Обе поверхности являются поверхностями вращения, оси вращения поверхностей пересекаются в точке О и лежат в одной плоскости. Эта плоскость параллельна фронтальной плоскости проекций и является плоскостью симметрии для заданных поверхностей. Следовательно, задачу можно решить способом концентрических вспомогательных сфер. Линия пересечения поверхностей вращения – пространственная кривая четвертого порядка.
3.Точки пересечения очерков поверхностей А и D принадлежат линии пересечения поверхностей, т. к. располагаются в плоскости симметрии и являются характерными точками линии пересечения. Центром концентрических сфер является точка пересечения осей вращения поверхностей – точка О.
4.Для определения величины минимальной вспомогательной сферы, из точки пересечения осей вращения О проводим перпендикуляры на очерковые образующие пересекающихся поверхностей. Минимальная сфера должна быть вписана в большую поверхность. В рассматриваемой задаче большей поверхностью является тор. Радиус ми-
нимальной сферы обозначим Rmin. Радиус максимальной сферы Rmax равен расстоянию от центра концентрических сфер О до наиболее удаленной точки пересечения очерков D.
5.Вспомогательные промежуточные сферы проводим произ-
вольным радиусом, но больше Rmin и меньше Rmax. Вспомогательная сфера пересекает каждую из заданных поверхностей по окружности, плоскость которой перпендикулярна оси вращения поверхности и проецируется на фронтальной плоскости проекций в прямую линию, перпендикулярную оси вращения поверхности. Проекции окружностей пересекаются в точках С и В, принадлежащих обеим поверхностям. Это искомые точки, принадлежащие линии пересечения поверхностей.
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 26 из 33 |

Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
6. Построенные фронтальные проекции точек А2, В2, С2, D2 соединим плавной видимой кривой линией.
Задание 4.2 Построить развертку поверхности Р (рис.4).
1. Для построения развертки поверхности, часть конуса ограниченную линией пересечения и верхним основанием начертим отдельно. Развертку прямого кругового конуса строим способом нормального сечения. Аппроксимируем поверхность конуса вписанной в него многогранной пирамидой. Для этого в круговое основание конуса впишем правильный двенадцатиугольник. Через вершины многоугольника проводим ребра пирамиды. Развертка прямого кругового конуса – часть кругового сектора, радиус которого равен величине очерковой образующей конуса S1 или S7. Очерковые образующие S1 и S7 проецируются в натуральную величину на фронтальную плоскость проекций, так как являются фронтальными прямыми. Длина дуги сектора равна периметру двенадцатиугольника, вписанного в кру-
говое основание 1121 – 2131 – 3141… – 101111 – 111121.
2.Натуральную величину образующих конуса SM, SH, SG, SF, SE определим способом вращения вокруг оси ОS, перпендикулярной горизонтальной плоскости проекций.
3.Построенные точки A, E, F, G, H, M, D соединим плавной кривой линией.
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 27 из 33 |
Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
α |
α |
Y
Y


 β
β



Рис. 1. Относительное положение прямой и плоскости, плоскостей
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 28 из 33 |
Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
||
|
α |
|
|
4 |
|
|
0 |
|
|
Рис. 2. Относительное положение поверхности и плоскости |
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 29 из 33 |
Кириллова Т.И., Елькина Л.Ю., |
Относительное положениегеометрических объектов |
|
Морозова Н.Н., Зигулев А.Г. |
||
|
||
Рис. 3. Относительное положение поверхностей. Способ вспомогательных секущих плоскостей |
||
ГОУ ВПО «УГТУ-УПИ» – 2005 |
Стр. 30 из 33 |
