Руководство ЛР ТМП. Редакция 8

После несложных преобразований, справедливых, если для всех диффузионных этапов v << vп,

приходим к следующему выражению:

Теперь его можно упрощать для отдельных частных случаев. Если в знаменателе можно пренеб-

речь всеми слагаемыми по сравнению с единицей, то реализуется кинетический режим. Уравнение связи в этом случае имеет вид:

В этом случае должна наблюдаться линейная зависимость в координатах v / [Mn] – (MnO)·[Si]0.5 / [Mn]. Если же лимитирующей стадией является диффузия марганца в металле, то в знаменателе самым большим слагаемым станет второе. В этом случае уравнение связи примет вид:

Если учесть, что предельная скорость диффузии марганца в металле пропорциональна ее концентрации: v[Mn] = k[Mn] · [Mn], то приходим к уравнению такого же вида, как для кинетического режима, но коэффициенты в нем имеют другой смысл:

В этом случае выявить режим процесса можно, меняя условия перемешивания, что не предусмот-

рено для моделируемой установки.

Наиболее сложный случай реализуется, когда наибольшим слагаемым в знаменателе формулы ()

является последнее. Здесь лимитирующей стадией может быть диффузия кремния в металле или оксида марганца в шлаке. В первом случае уравнение () может быть преобразовано к виду:

а во втором – к виду:

В зависимости от того, в каких координатах удается линеаризовать экспериментальные данные можно судить о лимитирующей стадии процесса.

Кинетическое уравнение реакции 5 имеет вид

С учетом связи объемных концентраций с поверхностными и приповерхностными приходим к со-

отношению вида:

51

Если лимитирующей стадией является диффузия оксида марганца в шлаке, то последнее уравне-

ние приводится к виду:

Для кинетического режима уравнение имеет такой же вид, но постоянные коэффициенты имеют другой смысл и, соответственно, другие обозначения.

Если лимитирующей стадией является диффузия марганца в металле, то уравнение приобретает вид:

Наконец, если затруднена доставка к межфазной границе оксида железа, то получается соотноше-

ние:

Константа равновесия реакции, выраженная через активности

(18.1)

является функцией только температуры.

Отношение равновесных концентраций марганца в шлаке и металле

(18.2)

называют коэффициентом распределения марганца, который, в отличие от 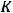, зависит от состава фаз и служит количественной характеристикой распределения этого элемента между шлаком и металлом.

2.6.2Модель процесса

Вимитационной модели рассмотрены три электродные полуреакции, которые могут проте-

кать между оксидным расплавом CaO – MnO – FeO – SiO2 – Al2O3 и жидким железом, содержа-

щим в качестве примесей Мn и Si. Сделано допущение о диффузионном режиме их протекания.

Учтена заторможенность диффузии частиц Fe2+ в шлаке, кремния в металле, марганца в обеих фа-

зах. Общая система уравнений, описывающая модель, имеет вид

52

(18.4)

(18.5)

(18.6)

(18.7)

(18.8)

где υј – скорость электродной полуреакции, ηj – поляризация, ij – плотность предельного тока диффузии, Dj – коэффициент диффузии, β – конвективная постоянная, Cj – концентрация.

Программа имитационной модели позволяет решить систему уравнений (18.4) – (18.8), что дает возможность установить, как изменяется объемная концентрация компонентов и скорости их перехода со временем при взаимодействии металла со шлаком. Результаты расчета выводятся на дисплей. Информация, получаемая с экрана монитора, включает в себя графическое изображение изменения концентраций основных компонентов, их текущие значения, а также значения темпера-

туры и константы конвекции (рисунок 8).

Блок-схема программы имитационной модели взаимодействия металла и шлака представ-

лена на рисунке 7. Программа работает в цикле, который прекращается только после истечения заданного времени моделирования (примерно 10 мин).

53

Рисунок 7 – Блок-схема программы имитационной модели

2.6.3 Порядок проведения работы

Изображение, генерируемое имитационной программой, представлено на рис 8 (правая па-

нель). В верхней части панели приводятся выборочные числовые значения измеряемых величин,

на графике отображены все значения, полученные в ходе моделирования процесса. В обозначени-

ях компонентов металлического и шлакового расплавов использованы принятые литервтуре ме-

таллургической тематики дополнительные знаки. Квадратные скобки обозначают принадлежность компонента металлическому расплаву, а круглые – шлаковому. Множители при обозначениях компонентов используются только для построения графика, их не следует учитывать при интер-

претации значений. Во время работы модели в каждый данный момент отображается только зна-

чение одной из измеряемых величин. Через 6 сек оно исчезает и появляется значение следующей величины. За этот промежуток времени надо успеть записать очередное значение. Для экономии времени рекомендуется неизменные цифры не записывать, например, ведущую единицу в значе-

нии температуры.

54

Рис 8. Изображение экрана монитора при выполнении работы № 18 на разных стадиях процессов.,

Через пять-шесть минут после начала работы установки произведите добавку предварительно прогретого оксида марганца в шлак, что реализуется при одновременном нажатии клавиши

Alt и цифровой клавиши на основной клавиатуре с номером Вашей установки.

2.6.4 Обработка и представление результатов измерений

Результаты экспериментов на промышленных установках, получение которых в работе реализуется на имитационной модели, как правило, отличаются от лабораторных испытаний одновременным изменением большого числа параметров и повышенной погрешностью результатов измерений, что затрудняет их интерпретацию и обсуждение. В этом случае приходится использовать для анализа максимально упрощенные модели и простейшие функциональные зависимости. Здесь очень важно хорошо представлять все используемые упрощения и границы их применимости. Результатом измерений в работе № 18 являются наборы дискретных значений концентраций основных реагентов в металлической ([Si], [Mn]) и шлаковой ((MnO), (FeO)) фазах, характеризующие их изменение со временем. Они дают возможность оценить численными методами скорости реакций 4 и 5, а также общую скорость перехода кремния. Реализация таких методов описана

55

во вводной части пособия. Анализ результатов становится намного проще и понятнее, когда вза-

мосвязи между всей совокупностью данных отражены на графиках. В данном случае ограничимся

4-мя графиками (диаграммами XY): 1 - зависимость температуры от времени (одна кривая), 2 - за-

висимости концентраций компонентов металла (кремния и марганца) от времени (две кривые), 3 -

зависимости концентраций компонентов шлака (оксиды марганца и железа) от времени (две кри-

вые) и 4 – зависимости скоростей перехода марганца и реакций 4 и 5, определенные по изменению содержаний кремния в металле и оксида железа в шлаке (три кривые). Методом наименьших квадратов следует оценить константы скоростей прямой и обратной реакций процесса 4 по урав-

нению (18.4) отдельно до и после увеличения содержания марганца в шлаке и погрешности опре-

деления этих величин. Учтите, что в уравнении (18.4) отсутствует свободный член.

Порядок обработки результатов

1.Ввести результаты ручной записи информации в файл электронных таблиц.

2.Вычислить скорости процессов по концентрациям кремния и марганца в металле и оксида железа в шлаке. Используйте значение массы металла 100 кг и не забудьте учесть стехиометрические множители. Площадь межфазной поверхности не учитывайте.

3.Построить на отдельных листах графики зависимостей температуры в агрегате и концентраций реагентов от времени, скоростей перехода кремния и отдельных процессов от времени.

4.Вычислить константы kf4 и kr4 процесса 4 по уравнению (18.4) до и после увеличения содержания марганца в шлаке и погрешности их определения.

5.Сделать выводы по полученным данным.

Зачетные результаты:

1.Правильно оформленные графики (четыре графика – восемь кривых) на отдельном листе электронных таблиц со всеми необходимыми подписями обозначениями.

2.Значения констант скоростей и погрешностей их определения.

3.Выводы по работе.

Контрольные вопросы

1.Почему возникает необходимость моделирования процессов производства стали?

2.Какова природа взаимодействия металла со шлаком и в чем это проявляется?

3.Какой потенциал называется стационарным?

4.Какой потенциал называется равновесным?

5.Что называется электродной поляризацией (перенапряжением)?

6.Что называется коэффициентом распределения марганца между металлом и шлаком?

7.От чего зависит константа распределения марганца между металлом и шлаком?

8.Какие факторы влияют на скорость перехода марганца из металла в шлак в диффузионном режиме?

9.Перечислите определяемые по результатам опытов физические величины.

10.Выберите комбинации величин для построения регламентированных в работе графиков (Ось Х, Ось Y)

11.Перечислите физические величины, определяемые по результатам опытов.

12.Перечислите ожидаемые наблюдения по результатам работы.

13.Укажите количество электронов в электродной полуреакции перехода марганца (кремния, железа) через границу металл-шлак.

56

14.Укажите формы существования реагентов (кремний, марганец, железо) в фазах, в которых они присутствуют.

15.Последовательно перечислите этапы восстановления марганца (железа, кремния) и механизмы их реализации.

57

Список литературы

1.Линчевский, Б.В. Техника металлургического эксперимента [Текст] / Б.В. Линчевский. –

М.: Металлургия, 1992. – 240 с.

2.Арсентьев, П.П. Физико-химические методы исследования металлургических процессов

[Текст]: учебник для вузов / П.П. Арсентьев, В.В. Яковлев, М.Г. Крашенинников,

Л.А. Пронин и др. – М.: Металлургия, 1988. – 511 с.

3.Попель, С.И. Взаимодействие расплавленного металла с газом и шлаком [Текст]: учебное пособие / С.И. Попель, Ю.П. Никитин, Л.А. Бармин и др. – Свердловск: изд. УПИ им.

С.М. Кирова, 1975, – 184 с.

4.Попель, С.И. Теория металлургических процессов [Текст]: учебное пособие / С.И. Попель,

А.И. Сотников, В.Н. Бороненков. – М.: Металлургия, 1986. – 463 с.

5.Лепинских, Б.М. Транспортные свойства металлических и шлаковых расплавов [Текст]:

Справочник / Б.М. Лепинских, А.А. Белоусов / Под. ред. Ватолина Н.А. – М.: Металлургия,

1995. – 649 с.

6.Белай, Г.Е. Организация металлургического эксперимента [Текст]: учебное пособие /

Г.Е. Белай, В.В. Дембовский, О.В. Соценко. – М.: Химия, 1982. – 228 с.

7.Панфилов, А.М. Расчет термодинамических свойств при высоких температурах [Электрон-

ный ресурс] : учебно-методическое пособие для студентов металлургического и физико-

технического факультетов всех форм обучения / А.М. Панфилов, Н.С. Семенова – Екате-

ринбург : УГТУ-УПИ, 2009. – 33 c.

8.Панфилов, А.М. Термодинамические расчеты в электронных таблицах Excel [Электронный ресурс] : методические указания для студентов металлургического и физико-технического факультетов всех форм обучения / А.М.Панфилов, Н.С. Семенова – Екатеринбург : УГТУ-

УПИ, 2009. – 31 с.

9.Краткий справочник физико-химических величин / Под. ред. А.А. Равделя и А.М. Пономаре-

ва. Л. : Химия, 1983. – 232 с.

58