Окончание табл. 12

Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Уральский Федеральный университет им. Б.Н. Ельцина «УПИ»

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Методичка по строительной механике.pdf

Скачиваний:

291

Добавлен:

23.02.2015

Размер:

2.3 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1615 16 > Следующая >>>

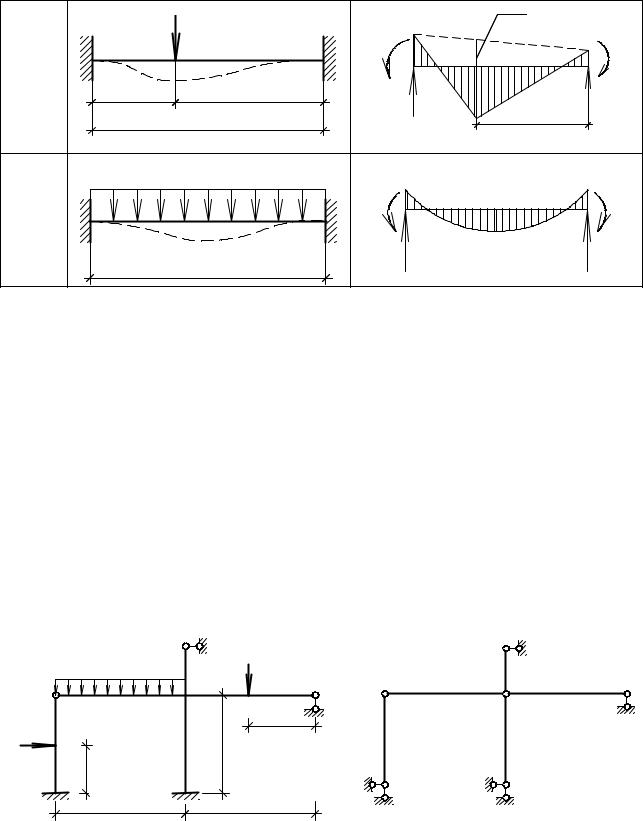
							Окончание табл. 12
			MA =uv 2Pl				vuPl
			MA =uv 2Pl					2
A	P	B						MB =u vPl
A	P	B
9	ul	vl
	ul	vl	RA					RB
	l		RA					RB
	l		RA =v 2(1+2u)P					vl
			RA =v 2(1+2u)P				R =u 2(1+2v)P
							B
	q		M =M = ql			2		RA =RB = ql
			M =M = ql					RA =RB = ql
			A	B	12			2	MB
			MA		12			2	MB
10			A					B
A	l	B	RA				ql 2	RB
	l		RA				24	RB

Порядок расчета рам методом перемещений аналогичен порядку расчета стержневых систем методом сил. При проведении кинематической проверки необходимо производить перемножение окончательной эпюры изгибающих моментов с единичной эпюрой, построенной в любой основной системе метода сил.

Пример решения задачи № 7. Расчет рамы со смещаемыми узлами

Расчетная схема рамы представлена на рис. 58.

Число жестких узлов nу = 1 (узел С), число независимых линейных перемещений определим по шарнирной схеме (рис. 59).

nл = 2У −С −С0 = 2 6 −5 −6 =1.

Степень кинематической неопределимости n = nу + nл =1 +1 = 2.

q= 3 êÍ/ì

Ð1 =8 êÍ

À	h/2	F
À		F
		l= 8 ì

h=6ì h/2

	E
Ð2 =6 êÍ	C
D	C
B	D
l/2
À	F

l= 8 ì

Рис. 58. Расчетная схема рамы

Рис. 59. Шарнирная схема рамы

Заданная рама два раза кинематически неопределима. Образуем основную систему, введя в узел С заделку, препятствующую возможному угловому смещению, в дополнительной связи возникает реакция, которую обозначим через Z1. Вторая дополнительная связь в виде горизонтального опорного стержня будет препятствовать линейному смещению узлов рамы (рис. 60). Реакция в дополнительном опорном стержне Z2.

	E		Канонические уравнения
	Z1	Ð2 =6 êÍ	метода перемещений запишутся
Z2	q= 3 êÍ/ì	Ð2 =6 êÍ	в виде
Z2		D	в виде
B	C		r11Z1 + r12 Z2 + R1P = 0;
Ð1 =8 êÍ			r11Z1 + r12 Z2 + R1P = 0;
	ÎÑ		r21Z1 + r22 Z2 + R2P = 0.
À	F

Рис. 60. Основная система метода перемещений

Для определения коэффициентов при неизвестных строим единичные эпюры. Первую эпюру получаем, придав единичное угловое перемещение в первую связь узел С (рис. 61). Изображаем деформированную схему рамы, на стержни которой со стороны растянутых волокон накладываем эпюры моментов балок из табл. 12 (схемы № 1 и 6). Определяем значения опорных моментов и реакций по формулам табл. 12.

Коэффициент r11 определяем из рассмотрения условия равенству нулю моментов в узле С: r11 − EJ − 83 EJ − 23 EJ − 83 EJ = 0, r11 = 1229 EJ .

Коэффициент r21 определяем из условия равенства нулю горизонтальных сил: r21 + 13 EJ − 16 EJ = 0, r21 = − 16 EJ.

		3	E
		8 EJ	EJ			r11
r	B		EJ		D	3		EJ
r						3
21						8 EJ
	2					8 EJ		3	EJ
	2	EJ					C	3
	3	EJ	3	1			C	8
			3	1		2
			8 EJ			2	EJ
	M 1		1 EJ		1	3	EJ
A		F	1 EJ	B	1	EJ			D
A		F	3	B	3				D

r	1
21	6 EJ
21

Рис. 61. Схема определения коэффициентов r11 и r21

Вторую единичную эпюру получим, если придадим единичное линейное перемещение во второй связи (рис. 62). Так же изображаем деформированную схему рамы, на стержни которой со стороны растянутых волокон накладываем эпюры из табл. 12 (балки № 2 и 7). Значения опорных моментов и реакций определяем по формулам табл. 12.

Коэффициент r22 определяем, рассматривая условие равенства нулю горизонтальных сил: r22 − 633 EJ − 333 EJ −1263 EJ = 0, r22 = 7229 EJ.

Коэффициент r12 определим, рассматривая условие равенства нулю момен-

тов в узле С:		r12	+	1	EJ −		1	EJ = 0,		r12	= −	1	EJ.
				3			6					6
	1							E
	1														r12
						1									r12
				EJ		1										1
r22	B					3							D			3 EJ
r22	B												D		C	3 EJ
															C
				EJ		1								1
				EJ		6								1	EJ
											M 2			6
											M 2
																3 EJ
	A	1					F			r22				B		3 3	D
		EJ 12						1	EJ				33		C	12	EJ
								1							C	12
								6						EJ		6 3
													6

Рис. 62. Схема определения коэффициентов r12 и r22

Для определения свободных членов канонического уравнения необходимо построить в основной системе эпюры от заданных внешних сил (рис. 63).

Из табл. 12 переносим эпюры моментов от силового воздействия (балки № 4 и 5), определяем численные значения опорных моментов и реакций.

				E
				24
R2P		B		9			R
R2P						D	R
						D		1P
			12	R1P	7,5	ql	2	3Pl	=9
			12			8	=24	16
		7,5				8		C
		7,5			R2P
		M P			R2P	B			D
	9	A		F	5P1		C
	9					=2,5
						=2,5
					16
		Рис. 63. Схема определения свободных членов R1P и R2Р
					70

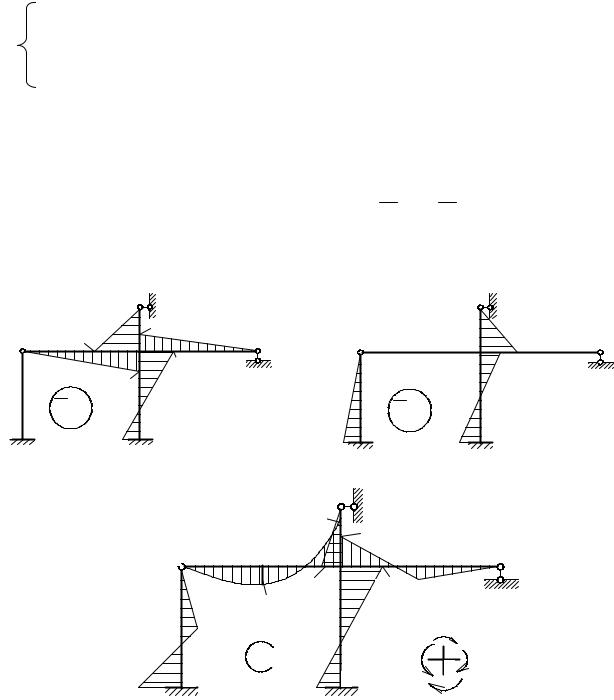
Рассматриваем равновесие узла С, определяем R1Р:

∑МC = 0, R1P +9 −24 = 0, R1P =15.

Рассматриваем условие равновесие горизонтальных сил:

∑x = 0, − 2,5 + R2 P = 0, R2P = 2,5.

Найденные значения коэффициентов подставляем в каноническое уравнение метода перемещений, решая систему уравнений определяем неизвестные Z1 и Z2.

29 EJZ1 −	1 EJZ2 +15	= 0,			7,65				21
12	6		Z1	= −	7,65	,	Z2	= −	21	.
− 1 EJZ1 +	29 EJZ2 +2,5 = 0.		Z1	= −		,	Z2	= −		.
− 1 EJZ1 +	29 EJZ2 +2,5 = 0.				EJ				EJ
6	72

Строим «исправленные» эпюры, для этого ординаты единичных эпюр умножаем на найденные значения Z1 и Z2 (рис. 64, а и б).

Для получения окончательной эпюры изгибающих моментов необходимо произвести сложение «исправленных» эпюр и грузовой эпюры, построенной в

основной системе метода перемещений Mок = M 1Z1 +M 2 Z2 +M P . Окончательная эпюра моментов в заданной системе представлена на рис. 64, в.

а)				E		б)		E
				E				E
	B	7,65		2,87	D	B			D
		7,65						6,97
								6,97
				5,1				3,49
			2,87
		M 1 Z1				M	2	Z
							2	2
A			2,55	F		A		F
			2,55

	1,74		3,49
в)	E
	E
	21,13
	IV	11,87
	IV			D
B	V	II	I
B	V	II
	C	8,59
	0,68	8,59	6,065

VI	13,44
	6,63	III	0,68
	6,63		0,68
VII	M îê	21,13	11,87
A		F	C
A	6,04	F	8,59
10,74	6,04		8,59
10,74

Рис. 64. Схема построения окончательной эпюры изгибающих моментов в заданной системе

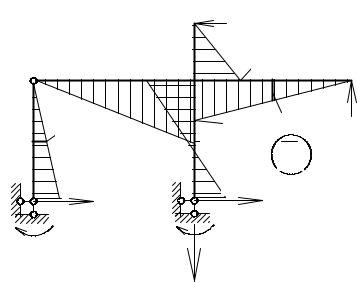
Условие равенства нулю моментов в узлах рамы является необходимым условием правильности построения окончательной эпюры моментов. В нашем

случае ∑МC =0,68 +11,87 +8,59 −21,13 =−0,01. Такое отклонение допустимо,

т. к. относительная погрешность составляет 0,02 %.

Произведем кинематическую проверку. Для этого построим единичную эпюру изгибающих моментов в основной системе метода сил и перемножим ее с окончательной эпюрой моментов в заданной системе с использованием таблицы выражений интеграла Мора для различных сочетаний эпюр (табл. 8).

Статическая неопределимость заданной системы:

n = 2Ш +C0 −3D = 2 +8 −3 2 = 4. Следовательно заданная рама имеет

4 «лишних» связи.

Для построения суммарной единичной эпюры удаляем «лишние» связи, их действие заменяем единичными усилиями и получаем основную систему метода сил (рис. 65).

				E	1
				E
	B		4	C	3	D
						1
					8	4
	0,5				8
	0,5				15	M S
						M S
A	1			F	1
A	HA	=1/6		F	HF	=5/6
1	HA	=1/6		1	HF	=5/6
1				1
					RF =2,875

Рис. 65. Суммарная единичная эпюра в основной системе метода сил

S M

ок

∑

∫

[10,74(−2 1 −0,5) − 6,63(−0,5 2 −1)] 3 +

0,5 6,63 3 +

6EJ

3EJ

21,13

15 8 − 1

15 8 − 1 3 0,68 3 +

[8,59(−4 2 +1)

−6,04(2 1 − 4)] 6 +

3EJ

6EJ

[11,87(−8 2 − 4) −6,065(−4 2 −8)] 4 +

6,065 4 4 =

6EJ

3EJ

= −

993,615

995,662

2,047

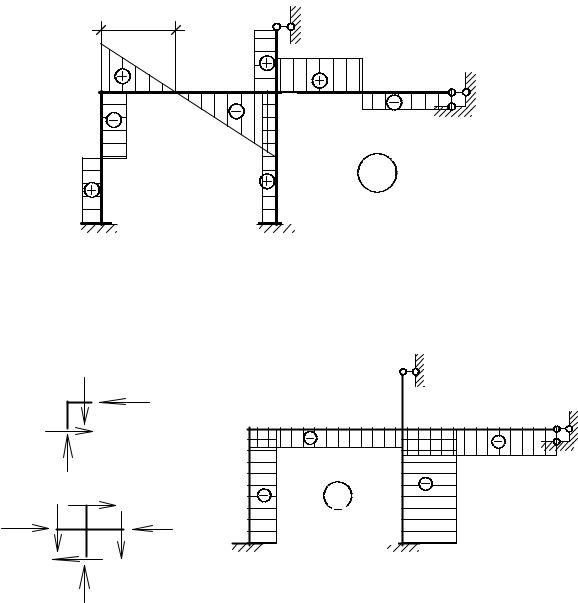
При перемножении эпюр по формуле ∑∫M SEJM ок грузовую эпюру из-

гибающих моментов на участке ВС предварительно расслоили на треугольную эпюру и параболу (рис. 66).

21,13

Относительная погрешность составила:

A − B

2,047

ε = min{A, B} 100%

= 993,615 100% ≈ 0,2% ,

13,44

21,13

что допускается.

По окончательной эпюре изгибающих

моментов строим эпюру поперечных сил по

участкам (рис. 67).

8 ì (ql 2)/8=24

Q = 0 −6,065

= −1,52

кН.

Рис. 66. Схема расслоения эпюры

Q = 6,065 −(−11,87) = 4,48 кН.

III

= 6,04 −(−8,59)

= 2,44 кН.

= 0 −(−0,68)

= 0,23 кН.

пр = −21,13 −0 − 3 8 = −14,64 кН.

Qлев

= −21,13 −0 + 3 8 =9,36 кН.

= 0 −6,63

= −2,21 кН. Q

= 6,63 −(−10,74)

=5,79 кН.

0,23

4,48

9,36

2,21

1,52

5,79

14,64

		III	Q
VII			Q
VII
A	2,44	F
	2,44

Рис. 67. Эпюра поперечных сил

Поперечная сила обращается в нуль на участке рамы ВС при

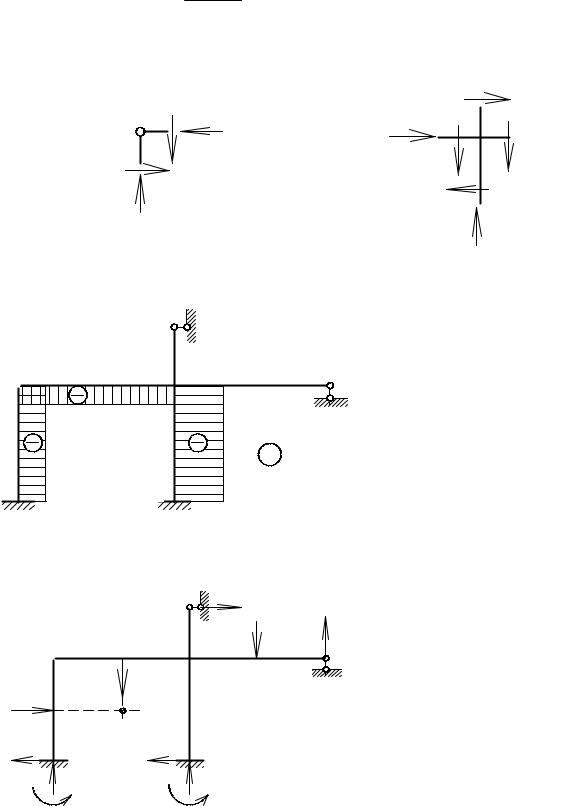
x0	=	9,36	=	9,36	= 3,12 м.
		q		3

В этом случае экстремальное значение изгибающего момента составит:

M max = 9,36 3,12 − 3 32,122 =14,6 кН м.

По эпюре поперечных сил построим эпюру продольных сил, используя метод вырезания узлов (рис. 68).

	Q V =9,36	Q IV =0,23	C
B	N V =2,21	N V =2,21	C
B	N V =2,21	N V =2,21	Q II =4,48
Q VI =2,21		Q V =14,64	Q II =4,48
		Q V =14,64	Q III =2,44

	N VI =9,36
	N VI =9,36
			N III =19,12

Рис. 68. Схема вырезания узлов для определения продольных сил

2,21

9,36

19,12

Рис. 69. Эпюра продольных сил

E	HE =0,23
			RD =1,52
C	P2	=6	D
C			D

ql=24

P1 =8

				G
HA =5,79 A				HF =2,44	F
R	=9,36	mA	=10,74	RF =19,12	m =6,04
A		mA	=10,74		m =6,04
					F

Рис. 70. Схема сил, приложенных к раме

Эпюра продольных сил представлена на рис. 69.

Приложим к раме все внешние нагрузки в том числе и реакции внешних связей (рис. 70).

Произведем статическую проверку.

∑y = 0.

RA + RF + RD −ql − P2 = 0.

9,36 +19,12 +1,52 −24 −6 = 0.

∑x = 0.

− H A + P1 + H E −F = 0.

−5,79 +8 +0,23 −2,44 = 0.

Проверки по силам выполняются.

∑mG = 0.

mA +mF − H A 3 − RA 4 − H F 3 + + RF 4 − H E 6 − P2 8 + RD 12 = 0

10,74 +6,04 −5,79 3 −9,36 4 −2,44 3 +19,12 4 −0,23 6 −6 8 +1,52 12 = =111,5 −111,51 = −0,01.

Относительная погрешность составляет примерно 0,01 %, что допускается.

Пример расчета рамы без линейного смещения узлов.

Схема рамы представлена на рис. 71. Число угловых перемещений равно числу жестких узлов nу = 2. Число независимых линейным перемещений определяем по шарнирной схеме (рис. 72).

nл = 2Y −C −C0 = 2 6 −5 −7 = 0. Таким образом, степень кинематической

неопределимости рамы составляет 2. Для предотвращения возможных угловых перемещений в жесткие узлы (В и С) устанавливаем жесткие заделки и получаем основную систему метода перемещений (рис. 73).

			E
		q=3 êÍ/ì	P2 =6 êÍ	h/2
B			P2 =6 êÍ	h/2
B
			C	l/2
P1 =8 êÍ		h=6ì		l/2
P1 =8 êÍ	h/2
	h/2			ÇÑ
				ÇÑ
A			F
		l=8 ì	l=8 ì

Рис. 71. Заданная расчетная схема рамы	Рис. 72. Шарнирная схема рамы

Z1	q=3 êÍ/ì	Z2	P =6 êÍ	В дополнительных связях воз-
			2	никают реакции Z1 и Z2, которые
			D	никают реакции Z1 и Z2, которые
	B	C		определим из канонических уравне-
P1 =8 êÍ				ний метода перемещений:

	ÎÑ	r11Z1	+ r12 Z2	+ R1P = 0,
A	F
		r21Z1	+ r22 Z2	+ R2P = 0.

Рис. 73. Основная схема метода перемещений

Для определения коэффициентов при неизвестных необходимо построить единичные эпюры, которые получаем путем последовательного введения единичного углового перемещения в наложенные связи.

Первая единичная эпюра (рис. 74) получена путем введения единичного углового смещения в первой связи. На деформированную схему рамы накладываем эпюры из табл. 12 (балка № 6).

Условие равновесия узла В:

∑M B = 0, r11	−	EJ	− 2EJ	= 0, r11		=	7EJ
		2	3				6
Условие равновесия узла С:
∑M C = 0, r21	−	EJ	= 0, r21	=	EJ .
		4			4
					E
B							2EJ
B							l
4EJ
h						C
	4EJ		1
		l

A	2EJ	M1	F
	h

		D
	r11		r21
B	EJ	EJ
B	2	EJ
	2	4	C
	2EJ	4	C
	2EJ
	3

Рис. 74. Схема определения коэффициентов r11 и r21

Придаем единичное угловое перемещение во второй связи, строим вторую единичную эпюрe, используя схемы балок из табл. 12 (рис. 75).

	4EJ	E
	l	3EJ
		h/2
B

2EJ	4EJ	C
	h	3EJ
l
		l
	M2

A	F	2EJ
		h

D		r22
		r22
			EJ
r12	EJ		3EJ
r12	EJ	C	8
B	2	C	8
B	2EJ
	2EJ
EJ	3

Рис. 75. Схема определения коэффициентов r22 и r12

Равновесие узла В:

∑M B = 0, r12 − EJ4 = 0, r12 = EJ4 .

Равновесие узла С:

∑M C = 0, r22 − EJ − 3EJ8 − 2EJ3 − EJ2 = 0, r22 = 6124EJ .

В основной системе строим эпюры изгибающих моментов от заданной внешней нагрузки и получаем грузовую эпюру (рис. 76). Рассматривая равновесие узлов определяем свободные члены канонических уравнений.

Равновесие узла В:

∑M B = 0, R1P +16 −6 = 0, R1P = −10.

Равновесие узла С:

∑MC = 0, R2P +9 −16 = 0, R2P = 7.

	ql	2	ql		2 E	3P2 l
	ql		ql
	12			12
	12			12		16
P1 h						16	D
P1 h							D
8	B					C
	B					C
			ql	2		5P2 l
		P1 h	ql	2		32	R2P
		P1 h	24			32	R2P
		8	24			R1P
		8				R1P

P1 h	A	M P	F	B	16	C
8					16	C	9
					16		9

Рис. 76. Схема определения свободных членов R1P и R2Р

Подставляем найденные коэффициенты и свободные члены в каноническое уравнение метода перемещений и определяем неизвестные Z1 и Z2.

7EJ

Z1 +

Z2 −10

= 0,

9,36

3,67 .

= −

Z1 +

61EJ

+ 7

= 0.

Строим «исправленные» эпюры, умножив ординаты единичных эпюр на соответствующие значения Z1 и Z2 (рис. 77).

		E			E
B		2,34	D	0,92	1,38	0,62
6,24		C	D	3,67		D
	1,17	C		B	C	2,45
	1,17			B	C	2,45
1,56	4,68			0,46	1,84
	4,68

	M Z		F	M2 Z2
A	1	1
	3,12			1,22	F
			A

Рис. 77. «Исправленные» эпюры моментов

Производим суммирование «исправленных» эпюр и грузовой эпюры мо-

ментов M 1Z1 + M 2 Z2 + M P = M ок.

Получаем окончательную эпюру изгибающих моментов в заданной системе (рис. 78). Необходимое условие – равенство нулю моментов сил в узлах рамы выполнено.

	12,24	16,5		E
	12,24			E
				10,38
12,24		V		II	I	D
	B	3,67	C	2,45
	VI	3,67		2,45
	VI	6,37		6,81
	4,44	6,37	III	6,81				3,67
			III			12,24		3,67
				Mîê	B	12,24		10,38
	VII			Mîê	B		16,5	10,38
2,88	A	1,22	F				16,5	C
2,88	A	1,22	F		12,24			C
					12,24			2,45
								2,45

Рис. 78. Окончательная эпюра изгибающих моментов в заданной системе

Статическая неопределимость заданной системы:

n = 2Ш +C0 −3D = 2 0 +9 −3 1 = 6. Следовательно заданная рама имеет 6

«лишних» связей.

Для построения суммарной единичной эпюры удаляем «лишние» связи, их действие заменяем единичными усилиями и получаем основную систему метода сил (рис. 79).

		E		1		1
				1
		5 C	3
B	16	5 C	3			D
					4	1
16			8		4
16			8
	19		16

A		F	1	MS
	22		1	1
	22			1
		1	1
			1

Рис. 79. Суммарная единичная эпюра в основной системе метода сил

∑∫

S M ок

[4,44(2 19 +22) −2,88(2 22 +19)] 3 +

6EJ

[4,44(2 19 +16) −12,24(2 16 +19)]

3 − (12,24 +16,5)

16 8 +

24 16 8 −

6EJ

2EJ

3EJ

−

3 3,67 3 +

[2,45(−2 5 +1) −1,22(2 1−5)] 6 +

3EJ

6EJ

[10,38(−2 8 −4) −6,8(−2 4 −8)] 4 +

6,81 4 4 =

2126,8

−

2126,75

0,05

6EJ

3EJ

При перемножении эпюр по формуле ∑∫

S M ок

грузовую эпюру из-

гибающих моментов на участке ВС предварительно расслоили на трапецию и параболу (рис. 80).

12,24	16,5		Относительная погрешность составила:
		ε =	A − B	100% =	0,05	100% ≈ 0,002%	,
	C		min{A, B}		2126,75
B	C	что допускается.
12,24	16,5		По окончательной эпюре изгибающих
12,24		моментов строим эпюру поперечных сил по
		моментов строим эпюру поперечных сил по
		участкам (рис. 81).
	(ql 2)/8=24		QI = 0 −6,81 = −1,7 кН.
				4

8 ì

= 6,81−(−10,38) =

QII 4 4,3 кН.

Рис. 80. Схема расслоения эпюры

QIII		=1,22 −(−2,45)	= 0,61 кН..	QIV =		0 −(−3,67)	=1,22	кН.
		6				3
Q	пр = −16,5 −(−12,24) − 3 8 = −12,53 кН.
V		8	2
		8	2
Q	лев = −16,5 −(−12,24) + 3 8 =11,47			кН.
V		8	2
		8	2
Q	VI	= −12,24 −4,44	= −5,56 кН. Q	VI	= 4,44 −(−2,88)		= 2,44	кН.
	VI	3		VI		3
		3				3

На участке ВС поперечная сила обращается в нуль, для сечения, располо-

женного на расстоянии x0		=11,47 / q =11,47 / 3 = 3,8 м экстремальное значение
изгибающего момента составит:
Mmax =11,47 3,8 −q 3,82 / 2 −12,24 =9,69 кН м.
	x0	1,22	E
11,47		IV	4,3
			I D
B		V
		C	II

VI	5,56		1,7
		12,53
			Q
		III

2,44 VII

0,61

Рис. 81. Эпюра поперечных сил

Методом вырезания узлов (рис. 82) и уравновешивая силы, определим значения продольных сил. Эпюра продольных сил представлена на рис. 83.

		QV =11,47				E
		NV =5,56
		B
	QVI =5,56			B		C	D
	QVI =5,56			B
		NVI =11,47			5,56		6,17
		QIV =1,22					6,17
		QIV =1,22			N
	QV =12,53		N	=6,17	N
	QV =12,53		N	=6,17
			CD		11,47		16,83
NV	=5,56	C		A	11,47	F	16,83
NV	=5,56			A		F

	Q =0,61	QII	=4,3
	III

		Рис. 83. Эпюра продольных сил
	NIII =16,83	Рис. 83. Эпюра продольных сил
	NIII =16,83
Рис. 82. Схема вырезания узлов рамы
		80

<<< < Предыдущая 1 2 3 4 5 6 7 8 9 10 11 12 13 1415 / 1615 16 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.07.2025168.45 Кб0методичка по селекции исправленный вариант (1).doc
#
11.11.2018315.9 Кб38Методичка по синтаксису.doc
#
22.02.2015305.15 Кб17методичка по социологии.doc
#
01.05.20251.01 Mб1методичка по статистике (для юристов).doc
#
22.02.201552.37 Кб720методичка по стилистике.docx
#
23.02.20152.3 Mб291Методичка по строительной механике.pdf
#
28.08.2019196.1 Кб7Методичка по технике и технологии.doc
#
01.05.20258.14 Mб0Методичка по ТИиК.doc
#
11.12.2018524.8 Кб140методичка по ТРИЗ и АРИЗ.doc
#
01.04.20251.34 Mб0методичка по ТЭА.doc
#
01.04.2025161.28 Кб1методичка по философии.doc