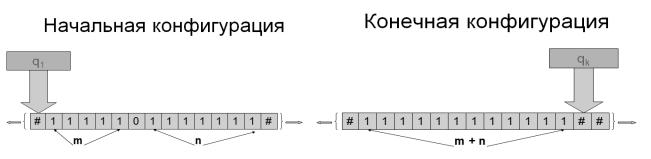
А = { #,1,0 } , где

# - отсутствие символа в ячейке ленты 1 - символ кода числа 0 – символ разделения двух чисел

Начальная конфигурация q1 a1 Конечная конфигурация a2 qk

Покажем, что число 4 характеризует сложность алгоритма сложения и не зависит от длины входных данных. Для этого запишем набор команд машины Тьюринга и найдем необходимое число внутренних состояний машины.

Понятие алгоритмически неразрешимой задачи

Появление точного понятия алгоритма позволило сформулировать алгоритмически не разрешимые проблемы, т.е. задачи, для решения которых невозможно построить алгоритм. Задача называется алгоритмически неразрешимой, если не существует машины Тьюринга (или рекурсивной функции, или нормального алгоритма Маркова), которая её решает. Например, неразрешимой оказалась проблема распознавания эквивалентности алгоритмов: нельзя построить алгоритм, который по любым двум алгоритмам (программам) выяснял бы, вычисляют они одну и ту же функцию или нет. Знание основных неразрешимостей теории алгоритмов необходимо для специалиста по информатике. Оно предостережёт его от увлечения глобальными прожектами всеобщей алгоритмизации точно так же, как знание основных законов физики предостерегает от попыток создания вечного двигателя.

Раздел 3 (Лекции 4-5)

Системы счисления

Ввопросах организации обработки информации на ЦВМ важное место занимают системы счисления, формы представления данных, специальное кодирование чисел.

Системой счисления называется совокупность приемов наименования и записи чисел.

Системы счисления различаются выбором алфавита, базисных чисел и правилами образования из них остальных чисел.

Алфавит систем счисления

Напомним, что алфавитом называется фиксированный конечный (упорядоченный) набор символов любой природы.

Всовременных системах счисления используется алфавит, включающий как арабские цифры 0, 1, 2, …9., так и буквы латинского алфавита, например, I, V, X, L, C, D, M и т.д.

Страница 11 из 45

Базисные числа систем счисления

Влюбой системе счисления каждому символу из набора алфавита – букве - приписывается базисное число. Например, в римской системе используются буквы I, V, X, L, С, D, М, которым соответствуют базисные числа 1, 5, 10, 50, 100, 500, 1000.

В16-чной системе счисления используется алфавит, состоящий из 9 арабских цифр и 6 латинских букв: 0, 1, 2, 3, …9, A, B, C, D, E, F. Базисные числа 0, 1, 2, 3, …9, 10, 11, 12,…15.

Аддитивно-мультипликативные системы счисления

Системы счисления, в которых любое число получается путем умножения и сложения базисных чисел, называются аддитивно-мультипликативными.

Все известные позиционные системы счисления являются аддитивно-мультипликативными. Особенно отчетливо аддитивно-мультипликативный способ образования чисел из базисных выражен в числительных русского языка, например пятьсот шестьдесят восемь (т.е. пять сотен плюс шесть десятков плюс восемь).

Позиционные системы счисления

Для изображения (или представления) чисел в настоящее время используются в основном позиционные системы счисления.

Система называется позиционной, если числовое значение каждой буквы алфавита зависит не только от приписанного ей базисного числа, но и от ее положения (позиции) в слове, изображающем число.

Основание позиционной системы счисления

Число К единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют

основанием позиционной системы счисления, а сама система счисления называется К-ичной.

Например, основанием десятичной СС является число К=10, троичной – число К=3, двоичной – число К=2, шестнадцатеричной – число К=16. В Древнем Вавилоне широко использовалась система счисления с основанием К=60.

Запись и изображение произвольного числа X в К-ичной позиционной системе счисления

Запись произвольного числа X в К-ичной позиционной системе счисления основывается на представлении этого числа в виде полинома:

где каждый коэффициент аi может быть одной из букв алфавита данной СС и изображается одним знаком.

Число X, представленное в К-ичной системе счисления, можно кратко записать писать в виде

аnаn-1...а1а0.а-1...а-т...

т.е. путем перечисления всех коэффициентов полинома с указанием позиционной точки.

Изображением числа X в К-ичной системе счисления является запись вида:

аnаn-1...а1а0.а-1...а -т... -к

где аi - любая буква алфавита данной системы счисления, количество букв в К-ичной системе счисления равно К.

Упорядоченной последовательности букв алфавита приписываются базисные числа: последовательные целые числа от нуля до К-1 включительно, 0 ≤ |аi | ≤ К-1, поскольку только в этом случае любое число Х может быть представлено в виде полинома.

Двоичная система счисления

В современной вычислительной технике, в устройствах автоматики и связи широко используется двоичная система счисления. Это система счисления с наименьшим возможным основанием. В ней для изображения числа используются только две цифры: 0 и 1.

Двоичная система удобна потому, что: простота технической реализации простота арифметических операций простота шифрования.

Система неудобна из-за громоздкости записи чисел. Однако для ЭВМ этот факт не имеет существенного значения

Арифметические операции в двоичной системе счисления

Страница 12 из 45

Постановка задачи перевода чисел из одной системы счисления в другую

При решении задач с помощью ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получить и окончательные результаты.

При рассмотрении правил перевода чисел из одной системы счисления в другую ограничимся только такими системами счисления, у которых базисными числами являются последовательные целые числа от 0 до Р-1 включительно, где Р — основание системы счисления.

Пусть известна запись числа Х в системе счисления с каким-либо основанием Р:

pnpn-1...p1p0.p-1...p-т...

где pi – известные буквы, 0 ≤ |pi | ≤ P-1.

Требуется найти запись этого же числа X в системе счисления с основанием Q:

qnqn-1...q1q0.q-1...q-т...

где qi – искомые буквы, 0 ≤ |qi | ≤ Q-1

Перевод целых чисел

Перевод дробных чисел

Понятие смешанной системы счисления

Страница 13 из 45

Вряде случаев числа, заданные в СС с основанием P, приходится изображать с помощью цифр другой СС с основанием Q, где Q < P.

Такая ситуация возникает, например, когда в ЭВМ, способной непосредственно воспринимать только двоичные числа, необходимо изобразить десятичные числа, с которыми мы привыкли работать.

Вэтих случаях используются смешанные системы счисления, в которых каждый коэффициент Р- ичного разложения числа записывается в Q-ичной системе.

Втакой системе P называется старшим основанием, Q – младшим, а сама система называется

(Q-P)-ичной.

Условие однозначности записи чисел в смешанной системе счисления

Для того чтобы запись числа в смешанной системе счисления была однозначной, для представления любой Р-ичной цифры отводится одно и то же количество Q-ичных разрядов, достаточное для представления любого базисного числа Р-ичной системы.

Условимся изображать принадлежность числа к (Q - Р)-ичной системе счисления с помощью

Двоично-десятичная система

В смешанной двоично-десятичной системе счисления для изображения каждой десятичной цифры отводится 4 двоичных разряда.

Например, десятичное число х = 729 в двоично-десятичной системе запишется в виде 0111 0010 1001. Здесь последовательные четверки (тетрады) двоичных разрядов изображают цифры 7, 2, 9 записи числа в десятичной системе.

Еще пример: 92510 = 1001 0010 0101(2 – 10)

Заметим, что 1001001001012 = 234110

Двоично-шестнадцатеричная система

Двоично-шестнадцатеричная система: 2E.916 = 0010 1110.1001(2-16)

Свойство смешанных систем и использование его в практических целях

Особого внимания заслуживает случай, когда Р = Ql, где / — целое положительное число.

В этом случае запись какого-либо числа в смешанной системе тождественно совпадает с изображением этого числа в системе счисления с основанием Q (что не имеет места в двоичнодесятичной системе в общем случае).

Двоично-восьмеричная система 57.58 =101 111.101 (2-8) = 101111.101 2

Двоично-шестнадцатеричная система 2E.916 = 0010 1110.1001(2-16) = 101110.10012 Двоично-четверичная система 232.34= 10 11 10. 11 (2-4) = 101110.11 2 Рассмотренное выше свойство используется на практике для сокращенной записи чисел, заданных

в системе счисления с небольшим основанием.

Для этого в исходной записи числа разряды объединяются вправо и влево от точки в группы длиной l (добавляя в случае необходимости левее старшей или правее младшей значащих цифр соответствующее количество нулей), и каждая такая группа записывается одной цифрой другой системы, основание которой равно соответствующей степени l исходного основания.

Цели кодирования информации

Цели кодирования информации Формирование представления информации называется ее кодированием. В более узком смысле

под кодированием понимается переход от исходного представления информации, удобного для восприятия человеком, к

представлению, удобному для хранения, передачи и обработки. В этом случае обратный переход к исходному представлению называется декодированием.

При кодировании информации ставятся следующие цели:

удобство физической реализации; удобство восприятия; высокая скорость передачи и обработки;

экономичность, т.е. уменьшение избыточности сообщения; надёжность, т.е. защита от случайных искажений;

сохранность, т.е. защита от нежелательного доступа к информации. Эти цели часто противоречат друг другу

Страница 14 из 45