
Численные методы. Интегрирование. Решение ОДУ
.pdf2345678901234567890123 |
|
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
2345678901234567890123 |
|
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ УРАЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ им. А. М. ГОРЬКОГО
РЕШЕНИЕ ЗАДАЧ ПО ЧИСЛЕННЫМ МЕТОДАМ
(численное интегрирование, решение обыкновенных дифференциальных уравнений)
Методические указания по курсу «Численные методы и математическое моделирование» для студентов 2 курса физического факультета
2345678901234567890123 |
|
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
234567890123456789012 |
3 |
Екатеринбург Издательство Уральского университета 2005
Методические указания подготовлены кафедрой компьютерной физики
Составитель В. А. Чернышев
Утверждено учебно-методической комиссией физического факультета 6 октября 2004 г.
Рассматриваются методы приближенного вычисления определенных интегралов, численного решения обыкновенных дифференциальных уравнений. Приводятся краткие теоретические сведения, необходимые для правильного применения рассматриваемых методов. Подробно разбирается ряд задач, предлагаемых студентам 2-го курса физического факультета на практических занятиях по курсу «Численные методы и математическое моделирование».
©Уральский государственный университет, 2005
©В. А. Чернышев, составление, 2005
1. ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ
Пусть функция f(x) непрерывна на [a; b], тогда определенный интеграл
b |
|
J = ò f (x)dx |
(1.1) |
a |
|
равен |
|
b |
|
J = ò f (x)dx = F(b) − F (a) |
(1.2) |
a
по формуле Ньютона – Лейбница. В тех случаях, когда первообразная функция F(x) не может быть выражена через элементарные функции или f(x) задана в виде таблицы, используют приближенные методы вычисления определенных интегралов. Рассмотрим несколько таких методов.
1.1. Методы левых, правых, средних прямоугольников
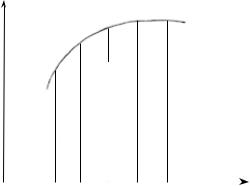
Определенный интеграл (1.1), согласно его геометрическому смыслу, численно равен площади S криволинейной трапеции, ограниченной осью абсцисс, двумя прямыми x = a и x = b и графиком функции y = f(x) (рис. 1).
Разобьем отрезок [a; b] на n равных частей точками x1, x2, x3, |
|||
…, xn – 1. Длина каждой части равна |
|
||
h = |
b − a |
. |
(1.3) |
|
|||
|
n |
|
|
Обозначим a = x0 è b = xn. Через точки x1, x2, x3, …, xn – 1 проведем прямые, параллельные оси ординат (см. рис. 1). Площадь S будет равна сумме площадей n элементарных криволинейных трапеций:
J = S = s1 + s2 + … + sn. |
(1.4) |
Y |
y = |
f(x) |
|
|
S
|
s1 |
s2 |
|
|
sn |
|
0 |
|
|
|
h |
|
X |
|
|
|
|
|
||
|
|
|
|
|
||
|
x0 = a x1 |
x2 |
|
b = xn |
||
Ðèñ. 1
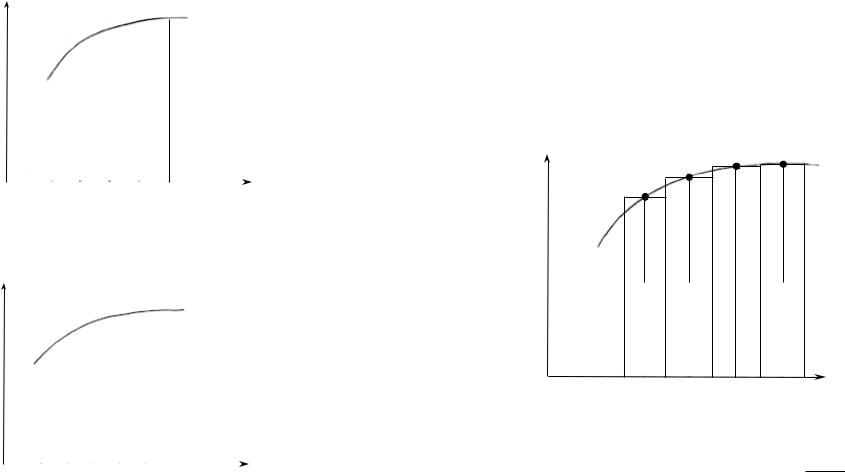
Чтобы найти приближенное значение площади S в правой ча- сти равенства (1.4), заменим сумму площадей n криволинейных трапеций суммой площадей n прямоугольников (рис. 2). Высоту i-го прямоугольника будем считать равной значению функции f(x) на левом конце отрезка [xi – 1; xi]:
−
J= S ≈ h f (x0 ) + h f (x1) + ... + h f (xn−1) = h å f (xi ).
i=0n 1
Правую часть последнего равенства обозначим
n−1 |
|
J ë.ï = h å f (xi ). |
(1.5) |
i=0
Формула (1.5) называется формулой левых прямоугольников. Если в качестве высоты i-го прямоугольника при нахождении
приближенного значения S брать значение функции f(x) на правом конце отрезка [xi – 1; xi] (рис. 3), получим
n
J = S ≈ h f (x1) + h f (x2 ) + ... + h f (xn ) = h å f (xi ).
i=1
4 |
5 |
Y |
|
x) |
|
y= |
f( |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
s2 |
|
|
|
sn |
|
|
0 |
|
|
h |
|
|
h |
|
|
X |
|
|
|
|
|
|
|
|
||
x0 = a x1 |
x2 |
|
b = xn |
||||||
|
|
|
|||||||
|
|
|
|
Ðèñ. 2 |
|
|
|||
Y |
|
|
|
|
|
|
y = f(x) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s1 |
s2 |
|
|
|
sn |
|
|
|
0 |
|
|
|
|
|
h |
|
|
|
X |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
x0 = a x1 x2 |
|
|
b = xn |
||||||
Ðèñ. 3.
Правую часть последнего равенства обозначим
n |
|
Jï.ï. = h å f (xi ). |
(1.6) |
i=1
Формула (1.6) называется формулой правых прямоугольников.
Заметим, что если функция f (x) выпукла вверх на отрезке интегрирования [a; b], то точное значение интеграла
Jë.ï. ≤ J ≤ Jï.ï.
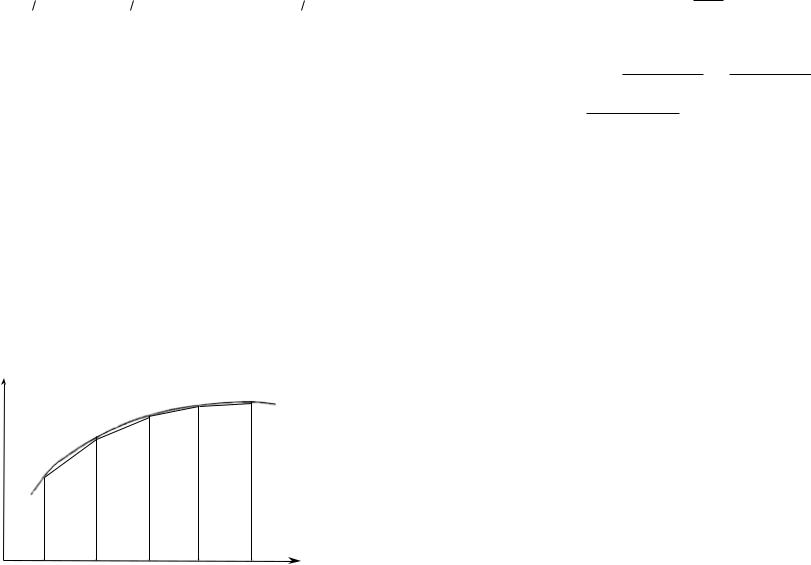
Теперь при нахождении приближенного значения S в качестве высоты i-го прямоугольника возьмем значение функции f(x) в середине отрезка [xi – 1; xi] (ðèñ. 4).
Y |
y = f(x) |
|
s1 |
|
s2 |
|
sn |
0 |
|
|
|
X |
|
|
|||
x0 = a x1/2 x1 x3/2 x2 |
b = xn |
|||
Ðèñ. 4 |
|
|||
Середина первого отрезка определится формулой x1 + x0 , второ-
|
|
|
|
|
|
|
|
|
2 |
|
|
ãî |
x2 + x1 |
, n-ãî |
|
xn + xn−1 |
. Для значения интеграла J получим при- |
||||||
|
|
|
|
||||||||
2 |
|
2 |
|
|
|
|
|
|
|
||
ближенное равенство |
|
|
|
|
|
|
|
||||
|
J = S ≈ h f ( |
x1 + x0 |
) + h f ( |
x2 + x1 |
) + |
... + h f ( |
xn + xn−1 |
). |
|||
|
|
|
|
||||||||
|
|
|
2 |
|
2 |
|
2 |
|
|||
Обозначим середины отрезков [xi – 1; xi] буквами x с дробными индексами:
6 |
7 |
x1 + x0 |
= x |
; |
x2 + x1 |
= x |
; ... ; |
xn + xn−1 |
= x |
n−1 2 |
. |
|
|
|
|||||||
2 |
1 2 |
|
2 |
3 2 |
|
2 |
|
|
|
|
|
|
|
|
|
|
Тогда правая часть приближенного равенства запишется в виде
n |
(1.7) |
Jñð.ïð = h å f (xi−1 2 ).
2 ).
i=1
Формула (1.7) называется формулой средних прямоугольников.
1.2. Метод трапеций
Криволинейную трапецию площади S разделим, как и в предыдущих случаях, на n криволинейных трапеций (ñì. ðèñ. 1).
J = S = s1 + s2 + … + sn.
Верхние концы отрезков, параллельных оси ординат, последовательно соединим прямыми линиями (рис. 5). Таким образом, мы заменим криволинейные трапеции прямолинейными. Основания i-й трапеции равны соответственно f(xi – 1) è f(xi). Высоты всех трапеций
Y |
y = f(x) |
|
|
s1 |
s2 |
sn |
0 |
|
|
X |
x0 = a |
x1 |
x2 |
b = xn |
Ðèñ. 5
h = b - a . n
Для приближенного значения интеграла запишем
J = S » h f (x0 ) + f (x1) + h f (x1) + f (x2 ) + ...
2 2 (1.8)
+ h f (xn−1) + f (xn ) . 2
Правую часть приближенного равенства обозначим
|
æ |
f (x |
) + f (x |
n |
) |
n−1 |
ö |
|
J òð |
ç |
0 |
|
|
|
÷ |
(1.9) |
|
|
2 |
|
|
|
||||
= h ç |
|
|
|
+ å f (xi ) ÷. |
|
|||
|
è |
|
|
|
|
i=1 |
ø |
|
Формула (1.9) называется формулой трапеций. Из равенства (1.8) следует, что Jòð = (Jë. ï+Jï. ï)/2.
1.3. Метод Симпсона
Так же, как и ранее, разделим криволинейную трапецию площади S на n элементарных криволинейных трапеций с помощью прямых, проходящих через точки x1, x2, x3, …, xn – 1 (см. рис. 1). Метод Симпсона основан на замене частей кривой y = f(x) не прямыми, как было в методах прямоугольников и трапеций, а дугами парабол, оси которых параллельны оси OY.
Перенесем начало координат в точку a, сохраняя направление осей. По сути, это замена переменной. Возьмем участок кривой y = f(x), соответствующий отрезку [x0; x2] (рис. 6). Площадь двух элементарных трапеций, соответствующих этому отрезку, –
2h
S1 = ò f (x)dx.
0
Часть LKM кривой y = f(x) см. рис. 6) заменим частью параболы, ось которой параллельна оси OY. Уравнение параболы
y = ax2 + bx + c. |
(*) |
8 |
9 |
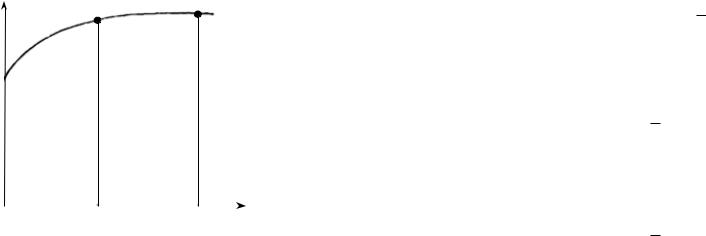
Y |
K(x1, y1) |
M(x2, y2) |
|
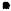 L(x0, y0)
L(x0, y0)
0 |
|
h |
h |
|
|
|
|
X |
|
|
|
|
||
x0 |
x1 |
x2 |
||
Ðèñ. 6
Коэффициенты a, b и c определим так, чтобы парабола проходила через точки L(x0, y0), K(x1, y1) è M(x2, y2). Координаты точек должны удовлетворять уравнениям
ìy0 = c |
|
|
|
|
|
ï |
= a h2 |
+ b h + c |
. |
(1.10) |
|
íy1 |
|||||
ï |
= a 4h |
2 |
+ 2b h |
+ c |
|
îy2 |
|
|
|||
Площадь фигуры, ограниченной параболой (*), осью OX и прямыми y = x0 è y = x2, равна
2h |
|
h |
|
|
|
2 |
2 |
|
|
ò(ax + bx + c) dx = |
|
|
(1.11) |
|
3 (8 a h + 6b h + 6c). |
||||
0 |
|
|
|
|
Ñдругой стороны, из системы (1.10) следует, что выражение
âскобках в правой части равенства (1.11) равно y0 + 4y1 + y2, поэтому
2òh(ax2 + bx + c)dx = h ( y0 + 4 y1 + y2 ). 3
0
Для площади двух элементарных криволинейных трапеций, соответствующих отрезку [x0; x2], запишем приближенное равенство
S1 » h ( y0 + 4 y1 + y2 ). 3
Для следующей пары элементарных криволинейных трапеций, соответствующих отрезку [x2; x4], заменив кривую y = f(x) частью параболы, получим
S2 » h ( y2 + 4 y3 + y4 ). 3
Аналогичные соотношения могут быть записаны для следующих пар криволинейных трапеций. Если число n элементарных криволинейных трапеций четное, n = 2k, то площадь S можно представить в виде суммы
S = S1 + S2 + ....+ Sk |
» |
h |
( y0 + 4 y1 + y2 + y2 + 4 y3 + y4 + ... |
|
|||
|
3 |
|
|
+ y2k − 2 + 4 y2k −1 + y2k ) .
Правую часть приближенного равенства обозначим
JÑèìï |
= |
h |
( y0 + y2k |
+ 4( y1 + y3 + y5 + ....+ y2k −1) + 2( y2 |
+ |
|
|
(1.12) |
|||||
|
3 |
|
|
|
||
y4 + 4 y6 + ....+ y2k −2 )) .
Формула (1.12) называется формулой Симпсона. Заметим, что число отрезков n, на которое в данном случае разбит отрезок интегрирования [a; b], должно быть четным: n = 2k.
10 |
11 |

1.4. Погрешность квадратурных формул
Соотношения для строгой оценки погрешности
В рассмотренных выше методах определенный интеграл заменялся конечной суммой
b |
f (x)dx ≈ |
å |
|
|
ò |
αi f (xi ), |
(1.13) |
||
|
|
|||
a |
|
i |
|
|
ãäå αi – некие числа. Соотношение (1.13) называется квадратурной формулой, его правая часть – квадратурной суммой. В зависимости от способа вычисления квадратурной суммы получаются разные методы приближенного интегрирования – прямоугольников, трапеций, Симпсона и т. д. Точки xi называются узлами, a числа αi – весовыми коэффициентами (весами) квадратурной формулы.
Погрешность при вычислении интеграла по квадратурной формуле равна
b
R = ò f (x)dx − åαi f (xi ).
a |
i |
Погрешность при интегрировании на отрезке [a; b] можно представить в виде суммы погрешностей на каждом элементарном отрезке [xi – 1; xi]:
|
n |
R = åri , n – число отрезков; |
|
|
i=1 |
x |
|
ri = òi |
f (x) dx − σi , ãäå σi – выражение, соответствующее квадратур- |
xi−1
ной формуле на отрезке [xi – 1; xi]. Разложим функцию f(x) в ряд Тейлора вблизи точки xi – 1/2 (середины отрезка [xi – 1; xi]):
f (x) = yi−1 2 |
+ yi′−1 2 |
(x − xi−1 2 ) + |
1 |
f ′′(ξi )(x − xi−1 2 )2 , |
|
||||
|
|
2 ! |
||
ξi (xi−1; xi ). |
|
|
|
|
Проинтегрируем обе части этого равенства на отрезке [xi – 1; xi]
xi |
|
|
|
24 |
|
|
|
|
|
|
|
|
ò |
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) dx = y |
i−1 2 |
h + |
1 |
f ′′(ξ |
|
) h3 |
, ξ |
|
(x |
; x |
). (1.14) |
|
|
i |
i |
|||||||||
|
|
|
|
|
|
|
i−1 |
i |
|
|||
xi |
1 |
|
|
|
|
|
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
Для метода средних прямоугольников σi = yi – 1/2 h, что соответствует первому слагаемому в правой части формулы (1.14). Поэтому
|
|
|
|
|
|
|
|
r = |
|
1 |
|
|
f ′′(ξ |
) h3 , |
|
ξ |
|
(x |
|
; x |
). |
|
(1.15) |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
i |
24 |
|
|
|
|
|
|
i |
|
|
|
|
|
i−1 |
|
i |
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Погрешность на всем отрезке [a; b] будет равна |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
h3 |
|
|
|
n |
|
′′ |
|
|
|
|
h3 |
|
n |
|
|
′′ |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
Rñð.ïð |
= |
|
å |
ri |
|
= |
|
|
|
å |
|
≤ |
å |
|
|
|
≤ |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
24 |
|
f (ξi ) |
24 |
|
|
f (ξi ) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
h3 n |
|
|
|
|
|
|
|
h3 |
|
|
|
|
(b − a) h2 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
≤ |
|
|
|
|
|
å |
M |
2 |
= |
|
|
|
n M |
2 |
= |
|
|
|
|
|
|
|
M |
2 |
, |
|
|||||
|
|
|
|
|
|
24 |
|
|
24 |
|
24 |
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ãäå M |
2 |
= max |
|
f ′′(x) |
|
|
|
– максимальное значение модуля второй про- |
|||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||
|
|
a≤x≤b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
изводной функции f(x) на отрезке [a; b]. Таким образом, погрешность метода средних прямоугольников оценивается по формуле
|
|
|
|
|
≤ |
(b − a) h2 |
|
. |
(1.16) |
|||||
|
|
|
|
|
|
|||||||||
|
R |
|
|
|
|
|
|
|
M |
2 |
||||
|
|
|
|
|
||||||||||
|
ñð.ïð |
|
|
|
24 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Аналогично можно получить для метода трапеций |
|
|||||||||||||
|
R |
òðàï |
|
≤ |
(b − a) h |
2 |
|
M |
2 |
; |
(1.17) |
|||
|
|
|
||||||||||||
|
|
|
|
|
|
|||||||||
|
|
12 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
метода левых (правых) прямоугольников |
|
|
|
|||||||||||
|
|
|
|
≤ |
(b − a) h |
|
|
|
(1.18) |
|||||
|
R ë.ï |
|
|
M1, |
|
|
||||||||
|
|
|
|
|
||||||||||
|
(ïð.ï) |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
12 |
13 |

метода Симпсона
RÑèìï |
|
£ |
(b - a) h4 |
M |
4 , |
(1.19) |
|
||||||
|
180 |
|
||||
|
|
|
|
|
|
ãäå M1 è Ì4 – максимальные значения модуля первой и четвертой производной функции f(x) на отрезке [a; b].
При выводе соотношения (1.17) для метода трапеций получа- ется выражение для погрешности на i-м отрезке:
ri = − h3 f ′′(ξi ). 12
Из сравнения этого выражения с соотношением (1.15) – погрешностью на i-м отрезке в методе средних прямоугольников, следует, что погрешность метода трапеций имеет другой знак и приблизительно вдвое больше по модулю. Поэтому можно записать уточненную формулу для приближенного вычисления интеграла:
J » |
(2 Jñð.ïð + J òðàï ) |
. |
(1.20) |
|
|||
3 |
|
|
|
Погрешность R зависит от шага разбиения h и имеет вид
R = O( hr)
(R есть O большое* îò hr при h ® 0). Показатель степени r называют порядком точности данного метода (данной квадратурной формулы).
Соотношения (1.16)–(1.19) дают строгую оценку погрешности, но их можно применять, когда существуют и могут быть вычислены соответствующие производные подынтегральной функции. Поэтому на практике часто используется способ приближенной оценки погрешности – метод двойного пересчета (метод Рунге), не связанный с вычислением производных.
* О понятии «O большое» см. прил., с. 52.
Учет погрешностей квадратурных формул методом двойного пересчета (метод Рунге)
Для погрешности метода средних прямоугольников на i-м элементарном отрезке мы записывали
r |
|
= |
1 |
f ¢¢(x |
) h3 , |
x |
|
Î(x |
; x |
|
); |
|||||||
i |
|
i |
|
|||||||||||||||
|
24 |
|
|
|
i |
|
|
|
|
|
|
i−1 |
i |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
ri |
= |
(b - a)3 |
|
f ¢¢(xi ). |
|
|
|
|
|
|
||||||||
24 n3 |
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если отрезок [a; b] разбить на 2n частей, получим |
||||||||||||||||||
r |
i |
= |
(b - a)3 |
|
f ¢¢(x* ), |
|
|
x* Î(x |
; x ). |
|||||||||
|
|
|
|
|||||||||||||||
|
|
24 ×8n3 |
|
|
|
|
i |
|
|
|
i |
i−1 |
|
i |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Для погрешности на всем отрезке [a; b] можно записать |
||||||||||||||||||
|
|
R n = |
(b |
- a)3 |
n |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
3 |
|
|
å f ¢¢(xi ); |
|
|
(1.21) |
||||||
|
|
|
|
|
|
24 n |
|
|
|
i=1 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
(b |
- a)3 |
2 |
n |
* |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
R 2 n = |
|
|
|
|
|
|
|
å f ¢¢(xi ). |
|
(1.22) |
||||||
|
|
|
|
|
|
|
3 |
|
|
|||||||||
|
|
|
|
|
|
24 ×8 n |
|
|
i=1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Будем считать, что значения производной f ²(x) мало меняются на отрезке [a; b], т. е.
f ²(x*i) » f ²(xi).
Тогда из соотношений (1.21) и (1.22) получим приближенное равенство
|
R 2n |
» |
Rn |
. |
1.23) |
|
|
||||
|
|
4 |
|
|
|
По определению, R2n |
= J – J2n, Rn = J – Jn (здесь J – точное зна- |
||||
чение интеграла). Поэтому |
|
|
|
|
|
R2n = Jn + Rn – J2n,
J2n – Jn = Rn – R2n.
14 |
15 |

С учетом приближенного равенства (1.23) получим
J2n – Jn » 3R2n, |
|
|
|
|
||||||
|
R 2 n » |
J2 n |
- Jn |
, |
|
|
|
|||
|
|
|
3 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
R 2 n |
|
» |
|
J2 n - Jn |
|
. |
(1.24) |
||
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Соотношение (1.24) дает приближенную оценку погрешности значения J2n, полученного по формуле средних прямоугольников. Для получения такой оценки расчет необходимо провести дважды: с разбиением отрезка интегрирования на n частей и на 2n частей.
Аналогичные оценки существуют для других квадратурных формул. Для формулы левых (правых) прямоугольников:
|
½R2n½»½J2n – Jn½, |
(1.25) |
||||||||
для формулы трапеций: |
|
|
|
|
|
|
|
|
|
|
|
R 2 n |
|
» |
|
J |
2 n - Jn |
|
, |
(1.26) |
|
|
|
|
|
|||||||
|
|
|
|
|||||||
|
|
|
|
3 |
|
|
||||
для формулы Симпсона: |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||
|
R 2 n |
|
|
» |
|
J |
2 n - Jn |
|
. |
(1.27) |
|
|
|
|
|
||||||
|
|
|
|
|
||||||
|
|
|
|
|
15 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
По соотношениям (1.24)–(1.27) оценивается погрешность зна- чения J2n: например, из формулы (1.27) для метода Симпсона следует, что число верных знаков значения J2n на единицу больше числа общих знаков, которые имеют Jn è J2n.
Пример 1. Вычислить с точностью 0,00001 интеграл
ϕ
F (j; k) = ò dt
0  1 - k 2 sin 2 t
1 - k 2 sin 2 t
ïðè j = 360 è k = 0,754710.
Р е ш е н и е. Воспользуемся методом Симпсона. Возьмем n = 4.
Поскольку a = 0, b = 360, |
h = |
b - a |
= 90 , |
h |
= 30 = 0,05235988 ðàä. |
|
Подынтегральная функция |
n |
3 |
|
|||
|
|
|
|
|||
|
f (t) = |
1 |
. |
|
||
|
1 - k 2 sin 2 t |
|
||||
|
|
|
|
|
||
Вычисления приведены в табл. 1. |
|
|
||||
|
|
|
|
|
Ò à á ë è ö à 1 |
|
|
|
|
|
|
|
|
i |
|
|
t 0 |
|
f(t ) |
|
|
|
|
i |
|
i |
|
|
|
|
|
|
|
|
0 |
|
|
0 |
|
1,00000 |
|
1 |
|
|
9 |
|
1,00704 |
|
2 |
|
|
18 |
|
1,02836 |
|
3 |
|
|
27 |
|
1,06443 |
|
4 |
|
|
36 |
|
1,11580 |
|
|
|
|
|
|
|
|
Согласно формуле (1.12)
JÑèìï = h [f (t0 ) + f (t4 ) + 4( f (t1 ) + f (t3 ) ) + 2 f (t2 )]= 3
= 0,6523205 .
Оценим погрешность этого результата методом Рунге. Для этого проведем вычисления при n = 2, взяв точки с i = 0, 2, 4. При этом h увеличится вдвое. Получим
JÑèìï = h¢ [f (t0 ) + 4 f (t2 ) + f (t4 )]= 0,6523230. 3
Таким образом,
JÑèìï = 0,6523205 ïðè n = 4; JÑèìï = 0,6523230 ïðè n = 2.
Согласно (1.27),
R 4 |
|
|
J4 - J 2 |
|
|
|
0,6523205 - 0,6523230 |
|
|
= 0,00000017. |
|
|
|
|
= |
|
|
||||||
|
|
|
|||||||||
» |
|
|
|||||||||
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
||||||
|
|
15 |
|
15 |
|
|
|
||||
|
|
|
|
||||||||
16 |
17 |

Пример 2. Вычислить по формуле трапеций и формуле Симпсона число p исходя из равенства
1 |
dx |
|
|
= p |
|
|
= arctg x |
10 |
|||
ò0 1+ x2 |
|||||
|
|
4 |
|||
|
|
||||
èопределить погрешность вычислений при n = 10.
Ðе ш е н и е. В данном примере b = 1, a = 0, n = 10, h = 0,1. Подынтегральная функция
f (x) = |
1 |
. |
1+ x2 |
Значения xi è yi = f (xi) приведены в табл. 2.
|
|
Ò à á ë è ö à 2 |
|
|
|
i |
xi |
yi |
|
|
|
0 |
0,0 |
1,00000000 |
1 |
0,1 |
0,99009901 |
2 |
0,2 |
0,96153846 |
3 |
0,3 |
0,91743119 |
4 |
0,4 |
0,86206897 |
5 |
0,5 |
0,80000000 |
6 |
0,6 |
0,73529412 |
7 |
0,7 |
0,67114094 |
8 |
0,8 |
0,60975610 |
9 |
0,9 |
0,55248619 |
10 |
1,0 |
0,50000000 |
|
|
|
По формуле Симпсона (1.12) получим
J |
|
= |
h |
[ y |
|
+ y + 4( y + y |
|
+ y + y |
|
+ y |
|
) + |
|
Ñèìï |
|
0 |
3 |
7 |
9 |
||||||||
|
3 |
|
10 |
1 |
5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
+ 2( y2 + y4 + y6 + y8 ) ] =0,785398154.
Исходя из формулы трапеций (1.9), имеем
J |
òð |
= h [ |
y0 + y10 |
+ y + y |
2 |
+ y |
3 |
+ y |
4 |
+ y + y |
6 |
+ y |
7 |
+ |
|
||||||||||||||
|
|
2 |
1 |
|
|
5 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ y8 + y9 ] = 0,784981497.
Сделаем точную оценку погрешности по формулам (1.19) и (1.17). В данном примере
|
|
f (x) = |
1 |
, |
|
|
||
|
|
1+ x2 |
|
|
||||
òàê ÷òî f ¢¢(x) = - 2 |
1- 3x2 |
|
; |
f IV (x) = + 24 |
1-10x2 + 5x4 |
. |
||
|
|
|
||||||
|
(1+ x2 )3 |
|
|
|
(1+ x2 )5 |
|||
На отрезке [a; b] = [0; 1] вторая и четвертая производные функции f (x) принимают максимальное по модулю значение в точке x = 0. Следовательно,
M2 = f ¢¢(0) = 2;
M4 = f IV (0) = 24.
По формулам (1.19) и (1.17) находим
R |
|
£ |
|
(b - a) h4 |
M |
4 |
= |
24 × 0,0001 |
= 0,000013, |
|||||
|
||||||||||||||
|
|
|
|
|
|
|
||||||||
Ñèìï |
|
|
180 |
|
|
|
|
180 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
R |
|
£ |
(b - a) h2 |
M |
2 |
= |
2 × 0,01 |
= 0,0017. |
||||||
|
||||||||||||||
|
|
|
|
|
|
|||||||||
òðàï |
|
|
|
12 |
|
|
|
12 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
||||
Поскольку точное значение интеграла p = 0,785398163..., ôàê-
4
тические погрешности
RÑèìï = 0,0000000099, Ròðàï = 0,000417.
Как видим, формулы для точной оценки погрешности дают завышенные результаты.
18 |
19 |
