лаб_р

4. Сделать несколько измерений величин y и C с помощью индикаторов 7 и 8 соответственно, последовательно увеличивая нагрузку равными ступенями P. Данные опыта занести в таблицу 1 (см. форму отчета). При выполнении опыта максимальная нагрузка Pmax на балку должна определятся из условия, чтобы возникающие в балке напряжения не превышали предела пропорциональности:

σmax = MWmax ≤ σпц . z

Для малоуглеродистой стали можно принять σпц = 200 МПа.

5.Определить опытный прогиб yоп как среднее арифметическое нескольких измерений y.

6.Найти опытный угол поворота ϕоп опорного сечения по формуле (3),

где С определяется как среднее арифметическое нескольких измерений С.

61

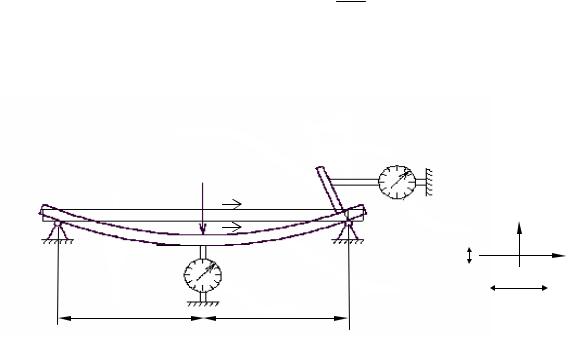
ЛАБОРАТОРНАЯ РАБОТА № 7

Отчет Определение перемещений при изгибе балки

Цель работы:……………………………………………………………………..….. …….…………….…………………………………………….……………………… Испытательная машина………………………………………………………………

Измерительные приборы……………..……………………………………………..

мм

Цена деления шкалы индикатора: Ku = ……….. дел

Схема нагружения балки и расположение измерительных приборов

P

Размеры балки и геометрические характеристики сечения

62

Результаты наблюдений

Теоретические значения максимального прогиба и угла поворота соответственно:

Выводы по работе…………………………………………………….……….……..

………………………………………………………………………….………....……

………………………………………………………………………….……...……….

………………………………………………………………………….………...…….

Отчет принял

……………………………..

63

ЛАБОРАТОРНАЯ РАБОТА № 8 Испытание на растяжение цилиндрической винтовой пружины

с малым шагом витка

Цель работы:

1)опытная проверка линейной зависимости между нагрузкой на пружину и её удлинением (закон Гука).

2)определение модуля сдвига материала проволоки и податливости пружины.

Общие сведения

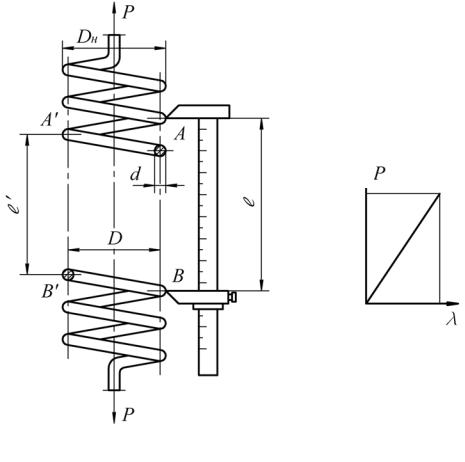
Цилиндрические винтовые пружины с малым шагом имеют углы наклона витков, не превышающие 8°-10°. Ввиду малости этих углов при расчетах таких пружин на прочность и жёсткость считают, что витки лежат в плоскости, перпендикулярной оси пружины. Кроме того, при определении удлинения (осадки при сжатии) пружины витки рассматривают в виде прямого стержня, испытывающего только кручение, а влиянием продольных, изгибающих деформаций, срезом, кривизной витков пренебрегают. С учётом этих упрощений формула для определения удлинений цилиндрической пружины, изготовленной из прутка круглого поперечного сечения (рис. 1, а), имеет вид:

где λ – удлинение пружины, то есть изменение длины пружины (её участка) вдоль оси; Р – сила, приложенная вдоль оси пружины;

D – средний диаметр пружины; d – диаметр проволоки пружины;

n – число витков пружины в пределах расчётной длины;

G – модуль упругости материала пружины при сдвиге.

64

Формула (1) справедлива в пределах упругих деформаций. Из неё следует, что между удлинением λ пружины и нагрузкой имеется линейная зависимость (рис. 1, б). Для проверки линейной зависимости (закона Гука) между удлинением и нагрузкой производится нагружение пружины равными ступенями и измеряются удлинения участка пружины, соответствующие этим приращениям нагрузки. Равным ступеням нагрузки должны соответствовать приблизительно равные приращения удлинений на измеряемом участке.

По результатам опыта строится график изменения удлинения λ пружины от нагрузки Р, из которого убеждаются в линейности зависимости между нагрузкой и удлинением пружины.

а

б

Рис. 1

Модуль сдвига материала пружины определяется на основе формулы (1):

λср d 4

65

Податливость − это деформация одного витка пружины, приходящийся на единицу нагрузки. Величина, обратная податливости, называется

жёсткостью.

Опытным путём коэффициент податливости находится как отношение измеренного удлинения участка пружины (всей пружины) к величине нагрузки, вызвавшей это удлинение, и числу витков участка (общему числу витков пружины), т.е.:

Порядок выполнения работы

1.Замерить диаметр сечения витка пружины d. Диаметр проволоки определяется штангенциркулем с точностью до 0,1 мм. Измерительный инструмент устанавливается перпендикулярно к оси витка пружины, чтобы исключить погрешность в определении диаметра проволоки, вызванную кривизной витка. Замеры сделать не менее 3 раз и в расчёт принять среднеарифметическое значение.

2.Определить средний диаметр пружины. Средний диаметр может быть определён как разность между наружным диаметром Dн и диаметром витка пружины d.

3.Подсчитать расчётное число витков, заключённое между точками А

иВ, А' и В' (рис. 1).Точки А, В и А', В' нанесены керном на диаметрально противоположных сторонах пружины.

66

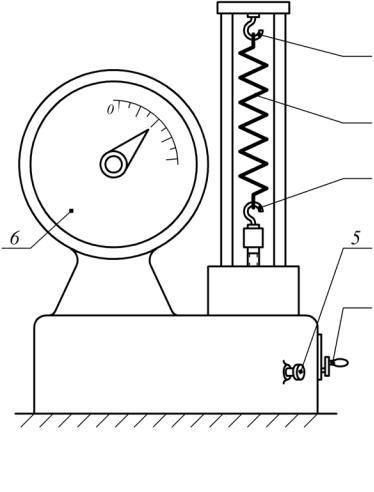
4. Установить пружину в испытательную машину марки МИП-100-2, предельная нагрузка которой 100 кг (1000 Н) (рис. 2). Пружина 1 подвешивается на крюки 2 и 3. Нижний крюк – подвижный. Расстояние между ними регулируется вращением рукоятки 4.

2

1

3

4

Рис. 2

5.Установить стрелку силоизмерителя на 6 на ноль путём вращения ручки настройки 5.

6.Дать начальное натяжение пружины Р0 = 10 кг (100 Н) вращением рукоятки 4.

7.Замерить штангенциркулем расстояние l0 и l′0 между точками А и В, А′

иВ'. В расчёт принять среднеарифметическое значение l0,ср (рис. 1).

8. Дать три дополнительных загружения пружины ступенями

Р = 25 кг с (250 Н). После каждой ступени приращения нагрузки производить замеры расстояний между точками А, В и А', В' и по среднему их значению li,ср

67

и l0,ср вычислять приращения отсчётов удлинения Δλi. Величина наибольшей нагрузки не должна превышать 90 кг с (900 Н).

9.Данные замеров и вычислений Δλi занести в таблицу (см. форму отчёта) и подсчитать среднее значение приращения удлинения измеряемого участка пружины Δλср.

10.По данным таблицы построить график изменения удлинения λ от нагрузки Р и провести его анализ.

11.Вычислить по формуле (2) модуль сдвига и сравнить его со средним значением G = 80 ГПа, которое принимается при расчётах.

12.Вычислить удлинение пружины λ по формуле (1) при нагрузке, указанной преподавателем.

13.При этой нагрузке определить удлинение пружины по формуле:

λоп = lср(р) − l0,ср.

14.Вычислить теоретический λ′ и опытный λ′оп коэффициенты податливости пружины по формулам (3) и (4).

15.Сравнить теоретическую и опытную величины коэффициентов податливости пружины:

δ = λ′−λоп 100% .

λ′оп

16. Оформить отчёт по прилагаемой форме.

68

ЛАБОРАТОРНАЯ РАБОТА № 8

Отчет

Испытание на растяжение цилиндрической винтовой пружины с малым шагом витка

Цель работы:……………………………………………………………………..….. …….…………….…………………………………………….……………………… Испытательная машина………………………………………………………………

Измерительные приборы……………..……………………………………………..

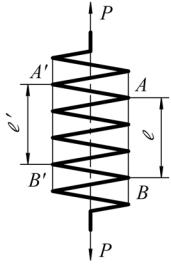
Схема нагружения и измерения

Данные пружины

1.Наружный диаметр Dн =…………………………..см

2.Диаметр проволоки d =……………………………см

3.Средний диаметр пружины D =..…………………см

4.Число витков на участке измерения n =………….шт

69

Таблица наблюдений

Диаграмма растяжения пружины

Р

λ

Определение модуля сдвига:

G = 8 P D3 n =…………………………=…………Па

λср d 4

Удлинение пружины, найденное аналитически:

λ = 8 P D3 n =……………………………=……….мм

G d 4

Удлинение пружины, определённое из опыта:

λоп = ………………..мм

70