
C2-2013-MIET
.pdf
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Тренировочные упражнения
84. В единичном кубе ABCDA1B1C1D1
найдите угол между прямой А1B1 и плос-
костью BDC1 .
85. В кубе ABCDA1B1C1D1 найдите угол между прямой AВ1 и плоскостью
ABC1.
86. В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой AA1 и плос-
костью BC1D .
87. В кубе ABCDA1B1C1D1 найдите тангенс угла между прямой AC1 и плос-
костью BCC1 .
88. В кубе ABCDA1B1C1D1 точка E –
середина ребра A1В1 . Найдите синус угла между прямой AE и плоскостью
ВDD1.
89. В кубе ABCDA1B1C1D1 точка E –
середина ребра A1В1 . Найдите синус угла между прямой AE и плоскостью
ВDC1 .
90. (ЕГЭ, 2012). В прямоугольном па-
раллелепипеде |
ABCDA1B1C1D1 , AB 2, |
AD AA1 1. |
Найдите угол между пря- |
мой AB1 и плоскостью ABC1 .
91. В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью AA1C и прямой A1В, если
AA1 3, AB 4, BC 4.
92. В прямоугольном параллелепипеде ABCDA1B1C1D1 найдите угол между плоскостью A1BC и прямой BC1, если
AA1 8, AB 6, BC 15.
93. В прямоугольном параллелепипеде
ABCDA1B1C1D1 , у которого AA1 4,
A1D1 6, C1D1 6 найдите тангенс угла между плоскостью ADD1 и прямой EF, проходящей через середины ребер AB и B1C1.
94. В прямоугольном параллелепипеде ABCDA1B1C1D1 , у которого AB 4,
BC 6, CC1 4 найдите тангенс угла между плоскостью АВС и прямой EF,
05.12.2012 |
41 |
проходящей через середины ребер AA1 и
C1D1 .
95. (ЕГЭ, 2011). В правильной четырехугольной призме ABCDA1B1C1D1 , сто-
роны основания которой равны 5, а боковые рёбра 7, найдите угол между прямой AB1 и плоскостью BDD1 .
96. В правильной треугольной призме ABCA1B1C1 , все стороны которой равны,
найдите угол между прямой AA1 и плос-
костью ABС1 .
97. В правильной треугольной призме ABCA1B1C1 , все рёбра которой равны 1,
точка D середина ребра A1В1 . Найдите синус угла между прямой AD и плоскостью BСC1 .
98. В основании прямой призмы MNKM1N1K1 лежит прямоугольный треугольник MNK, у которого угол N равен 90 , угол M равен 60 , NK 18. Диагональ боковой грани M1N составляет угол 30 с плоскостью MM1K1 . Найдите высоту призмы.
99. В основании прямой призмы ABCA1B1C1 лежит прямоугольный треугольник АВС, в котором угол С равен
90 , угол А равен 30 , AC 10
 3 . Диагональ боковой грани B1C составляет угол 30 с плоскостью AA1B1 . Найдите высоту призмы.
3 . Диагональ боковой грани B1C составляет угол 30 с плоскостью AA1B1 . Найдите высоту призмы.
100. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 3, а высота равна 1. Найдите угол между прямой F1B1 и плоско-
стью AF1C1 .
101. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, найдите угол между прямой AB1 и плоскостью ACE1.
102. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, точка G – середина ребра A1В1 . Найдите синус угла между прямой AG и плоскостью BСС1 .
www.abiturient.ru

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
103. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, точка G – середина ребра C1D1 . Найдите синус угла между пря-
мой AG и плоскостью BСС1 .
104. В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 , все рёбра которой равны 1, точка G – середина ребра A1В1 . Найдите синус угла между пря-
мой AG и плоскостью BDD1.
105. (МИОО). В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1 сторона основания равна 7, а высота равна 1. Найдите угол между прямой F1B1 и
плоскостью AF1C1 .
106. (ЕГЭ, 2010). В правильной треугольной пирамиде SABC с основанием
ABC известны ребра: AB 20
 3 , SC 29. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и ВС.
3 , SC 29. Найдите угол, образованный плоскостью основания и прямой, проходящей через середины ребер AS и ВС.
107. (ЕГЭ, 2010). В правильной треугольной пирамиде SABC с основанием
ABC известны |
рёбра: |
AB 12 3 , |
SC 13. Найдите |
угол, |
образованный |
плоскостью основания и |
прямой AM , |
|
где M точка пересечения медиан грани
SBC .
108.В правильной треугольной пирамиде SABC с основанием ABC сторона основания равна 2, а боковое ребро равно 3. Найдите угол между плоскостью BSC и прямой MN, где точка N – середина ребра AC, а точка M лежит на ребре SB так, что BM 1.
109.Дана правильная треугольная пирамиде ABCD, сторона основания и вы-
сота которой равны 6
 3 и 4 соответственно. Найдите угол между прямой EF и плоскостью основания ABC, если F середина ребра DB, а E лежит на AD так,
3 и 4 соответственно. Найдите угол между прямой EF и плоскостью основания ABC, если F середина ребра DB, а E лежит на AD так,
что AE : ED 3:1.
110. (МИОО). В правильной треугольной пирамиде SABC с основанием
ABC сторона основания равна 6
 3, а боковое ребро равно 10. Найдите угол между плоскостью АВС и прямой МN, где
3, а боковое ребро равно 10. Найдите угол между плоскостью АВС и прямой МN, где
05.12.2012 |
42 |
точка N – середина ребра АС, а точка М делит ребро BS так, что BM : MS 2:1.
111.В правильной четырехугольной пирамиде SABCD , все рёбра которой равны 1, найдите косинус угла между прямой AB и плоскостью SAD.
112.(ЕГЭ, 2011). В правильной четырехугольной пирамиде SABCD, в которой AB 3, SA 7, точка E середина ребра SB . Найдите угол между прямой CE
иплоскостью SBD.
113.В правильной четырехугольной пирамиде MABCD , все ребра которой равны 1, точка E середина ребра MC. Найдите синус угла между прямой DE и плоскостью AMB .
114.В правильной шестиугольной пирамиде MABCDEF, стороны основания
которой равны 1, а боковые рёбра равны 4, найдите синус угла между прямой BC
иплоскостью EMD.
115.В правильной шестиугольной пирамиде SABCDEF, боковые рёбра которой равны 2, а стороны основания – 1, найдите косинус угла между прямой АС и плоскостью SAF.
www.abiturient.ru
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
1.7.Угол между плоскостями
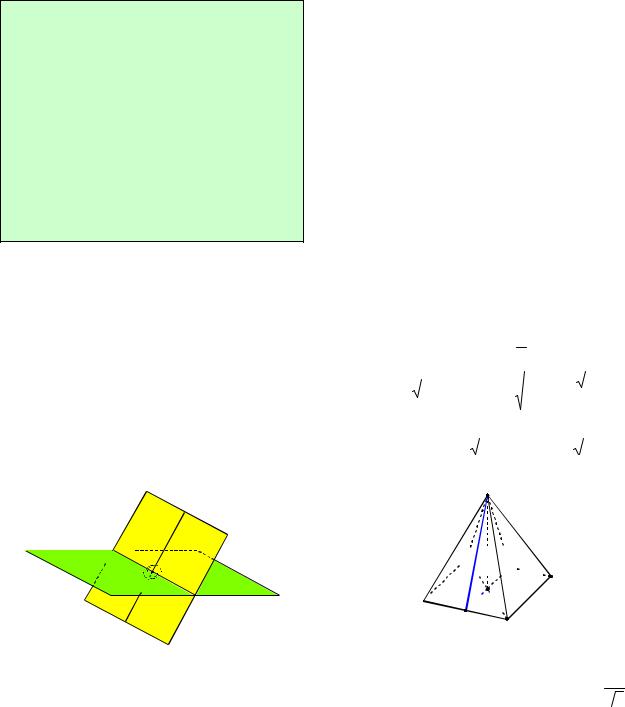
Двугранный угол, образованный полуплоскостями измеряется величиной его линейного угла, получаемого при пересечении двугранного угла плоскостью, перпендикулярной его ребру.
Величина двугранного угла принадлежит промежутку (0 , 180 ).
Величина угла между пересекающими-
ся плоскостями принадлежит проме-
жутку (0 , 90 ].
Угол между двумя параллельными плоскостями считается равным 0 .
Построение линейного угла двугранного угла или поэтапновычислительный метод
Рассматриваемый метод позволяет находить поэтапно искомый угол при решении известных задач, к которым сводится данная задача. Перечислим типы этих задач, связанных с нахождением угла:
●между пересекающимися прямыми a
иb, лежащими в рассматриваемых плоскостях и перпендикулярными их линии пересечения (см. рис. 63);
ствующий линейный угол строится с помощью двух перпендикуляров a и b, проведенных в указанных плоскостях к прямой их пересечения, а его величина в дальнейшем находится либо из некоторого прямоугольного треугольника, либо из некоторого треугольника с применением теоремы косинусов.
Пример 54. В правильной четырехугольной пирамиде SABCD , все рёбра которой равны 1, найти двугранный угол между основанием и боковой гранью.
Решение. Пусть E и K – середины ребер AD и BC соответственно, О – центр основания ABCD (см. рис. 64). Тогда SE AD, EK AD и поэтомуSEK – линейный угол данного двугранного угла.
Так как AD 1, OE 1 , SD 1, то
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
||
|
|
|
|
|
|
|
|
1 |
1 |
3 |
|||||||||
SE |
SD2 ED2 |
||||||||||||||||||
|
2 |
|
|
||||||||||||||||
|
|
OE |
|
4 |
|
|
|
|
|
||||||||||
cos |
|
1 |
|
, arccos |
|
1 |
|
. |
|||||||||||
|
|
|
|
|
|
|
|||||||||||||
|
|
SE |
3 |
|
|
|
|
|
|
|
3 |
|
|
|
|||||
S


 c
c
 A
A
Рис. 63
●между прямыми, параллельными прямым a и b или между b и прямой, параллельной a;
●между плоскостями, параллельными данным плоскостям и или между
и плоскостью, параллельной ;
●между перпендикулярами к данным плоскостям.
Решение задачи этим методом сводится непосредственно к построению линейного угла двугранного угла, образованного пересекающимися плоскостями и, и вычислению его значения. Соответ-
05.12.2012 |
43 |
B

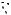



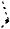
 K
K

 C
C
A



 O
O

E
D
Рис. 64
Ответ: arccos 1 .  3
3
Пример 55. В правильной шестиугольной пирамиде, стороны основания которой равны 1, а боковые рёбра равны 2, найти косинусы двугранных углов при основании и при боковом ребре.
Решение. Рассмотрим пирамиду MABCDEF. Поскольку пирамида правильная, то равны все ее двугранные углы при основании и равны все углы между любыми ее смежными боковыми гранями. Найдем, например, угол между
www.abiturient.ru
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
плоскостью основания и боковой гранью MAF и угол между боковыми гранями
FME и MDE (см. рис. 65).
M
C

 D
D N
N

 K
K 
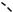
B 







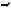



 E
E
 O
O
A L F
Рис. 65
Прямая AF – ребро двугранного угла MAFЕ. Пусть O – центр основания, тогда MO – высота пирамиды. Пусть L – середина отрезка AF, тогда ML – апофема грани AMF,
|
|
4 |
1 |
|
15 |
. |
|
ML |
AM2 AL2 |
||||||
|
|
||||||
|
4 |
2 |
|
||||
По теореме о трех перпендикулярах прямая LO перпендикулярна AF. Следовательно, MLO – линейный угол дву-
гранного угла MAFB. LO 3, так как
2
является высотой равностороннего треугольника AOF со стороной 1. Из прямоугольного треугольника LMO находим
cos MLO |
LO |
|
3 |
|
2 |
|
|
1 |
|
. |
||
|
2 |
|
|
|
|
|
|
|||||
|
ML |
|
15 |
5 |
|
|
||||||
Прямая ME – ребро двугранного угла FMED. В треугольниках FME и MDЕ проведём высоты к стороне ME из точек F и D соответственно. ПосколькуFME DME , то эти высоты «сойдутся» в одной точке N. Следовательно,DNF – линейный угол двугранного уг-
ла FMED.
Из равенства треугольников FME и MDЕ следует равенство высот FN и DN. Найдем FN. Для этого вычислим площадь треугольника FME. Поскольку апофема
05.12.2012 |
44 |
грани |
|
FME |
равна ML |
15 |
, |
SFME |
||||||||
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
||||
|
1 |
|
|
|
15 |
|
1 |
|
15 |
|
, то высота FN, опущен- |
|||
|
|
2 |
|
4 |
|
|||||||||
2 |
|
|
|
|
|
|
|
|
|
|||||
ная на ME, равна:
FN 2SFME 
 15 .
15 .
ME 4
Далее, рассмотрим равнобедренный треугольник FDN. В нем FD 2LO 
 3. Косинус угла DNF можно найти, воспользовавшись теоремой косинусов для стороны DF:
3. Косинус угла DNF можно найти, воспользовавшись теоремой косинусов для стороны DF:
cos FND FN2 DN2 FD2 3 .
2 FN DN |
5 |
Таким образом, искомые косинусы двугранных углов при основании и при
боковом ребре равны |
1 |
|
и |
3 |
|
соответ- |
||||||
|
|
|
|
|
||||||||
5 |
5 |
|
|
|
|
|
|
|||||
ственно. |
|
|
|
|
1 |
|
|
3 |
|
|||
Ответ: |
|
|
и |
. |
||||||||
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
5 |
5 |
|
|||
Так как в подобных телах соответствующие углы равны, а линейные элементы (стороны, высоты, медианы и т.п.) пропорциональны, то при вычислении углов в какой-либо конфигурации (обычно в треугольнике) важно учитывать лишь отношение длин соответствующих отрезков. Поэтому, если все линейные элементы конфигурации зависят от одного параметра, то можно принимать значение этого параметра равным какомунибудь числу. В частности, в кубе при нахождении угловых величин часто полагают длину его ребра равным единице.
Пример 56. В кубе ABCDABC1 1 1D1
найти угол между плоскостями сечений
ABC1 1D и CB1AD1 .
Решение. Пусть ребро куба равно 1. Прямая B1D – линия пересечения плос-
костей сечений ABC1 1D и CB1AD1 , так как B1 и D – их общие точки (см. рис. 66).
В прямоугольных треугольниках B1AD1 и
BC1 1D проведем высоты к гипотенузе
www.abiturient.ru
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
B1D из точек A1 и C1 соответственно.
Поскольку треугольники B1A1D и B1C1D
равны, то эти высоты «сойдутся» в одной точке N. Следовательно, A1NC1 – ли-
нейный угол двугранного угла A1B1DC1 .
B1 C1
A1

 D1
D1 



 N
N
 B
B 












 C
C
A D
Рис. 66
Поскольку прямоугольные треугольники B1A1D и B1C1D равны, то равны и высоты A1N и C1N , опущенные на гипоте-
нузу B1D. Длины указанных высот можно
найти, например, через площадь любого из этих треугольников:
A1N C1N 
 2 . 3
2 . 3
Далее, рассмотрим равнобедренный
треугольник AC1 1N . В нем AC 2 .
1 1
Найдём угол A1NC1, воспользовавшись теоремой косинусов для стороны AC1 1 :
cos ANC |
|
AN2 C N2 AC2 |
|||||||||||||||||||||
1 |
|
|
|
1 |
|
|
1 1 |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
2 A1N C1N |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
2) |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
3 |
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,5. |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Отсюда A1NC1 2 . 3
Следовательно, искомый угол между плоскостями сечений A1B1D и B1C1D ра-
вен . 3
Ответ: . 3
05.12.2012
Пример 57. В правильной треугольной призме ABCABC1 1 1 боковое ребро равно b,
а сторона основания a. Найти косинус угла между плоскостями ABC1 и ABC1 1 .
Решение. Построим линию пересечения
плоскостей ABC и ABC (см. рис.67). |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Диагонали |
AC1 |
|
|
M |
|
|
B1 |
|
|
|
|
|
||||||||||
и A1C в боковой |
|
A1 |
|
|
|
|
|
|
|
|
|
|
C1 |
|||||||||
грани |
AAC C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
призмы |
пересе- |
|
|
|
|
|
|
|
|
|
|
E |
|
|
|
|||||||
каются в точке D |
|
|
|
|
|
D |
|
N |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
и |
делятся |
этой |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
точкой пополам. |
|
|
|
|
|
|
|
B |
|
|
|
|
C |
|||||||||
Аналогично, |
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
диагонали BC1 и |
|
|
|
Рис. 67 |
|
|
|
|||||||||||||||
B1C в боковой |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
грани BB1C1C призмы пересекаются |
в |
|
||||||||||||||||||||
точке E и также делятся этой точкой по- |
|
|||||||||||||||||||||
полам. Точки D и E – общие точки плос- |
|
|||||||||||||||||||||
костей ABC и ABC, поэтому прямая DE |
|
|||||||||||||||||||||
|
|
1 |
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
является линией их пересечения. Кроме |
|
|||||||||||||||||||||
того, отрезок DE является средней линией |
|
|||||||||||||||||||||
равнобедренных треугольников ABC1 и |
|
|||||||||||||||||||||
ABC, а значит, DE || AB и DE || |
A B . |
|
|
|
||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
Рассмотрим |
равнобедренные |
тре- |
|
||||||||||||||||||
угольники C1DE и CDE. |
Они равны по |
|
||||||||||||||||||||
трем сторонам. Проведем в этих тре- |
|
|||||||||||||||||||||
угольниках медианы C1N и CN к общему |
|
|||||||||||||||||||||
основанию |
DE. |
|
Тогда |
C1N DE |
и |
|
||||||||||||||||
CN DE . Следовательно, |
C1NC – ли- |
|
||||||||||||||||||||
нейный угол двугранного угла C1DEC . |
|
|
|
|||||||||||||||||||
|
Найдем теперь косинус угла C1NC. С |
|
||||||||||||||||||||
этой целью рассмотрим равнобедренный |
|
|||||||||||||||||||||
треугольник C1NC. В |
нем |
C1N |
|
|||||||||||||||||||
CN |
CM |
|
|
CB12 MB12 |
|
|
|
|
|
3a2 |
4b2 |
|
, |
|
|
|||||||
2 |
|
|
|
2 |
|
|
|
|
|
|
4 |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
CC1 b. Воспользовавшись теоремой ко- |
|
|||||||||||||||||||||
синусов для стороны CC1 , получим: |
|
|
|
|||||||||||||||||||
cos C NC |
C N2 |
CN2 CC |
2 |
|
|
3a2 4b2 |
. |
|||||||||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
3a2 4b2 |
||||||||||||||
|
1 |
|
|
|
2 C N CN |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В рассматриваемом примере требуется найти косинус угла между плоскостя-
ми ABC1 и ABC1 1 . Встает закономерный вопрос. Нашли ли мы косинус того угла,
45
www.abiturient.ru
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
который требуется в условии, или же нам необходим косинус смежного с ним угла C1NM (кстати, на рис. 67 через обозначена величина именно этого угла)? На этот вопрос можно ответить следующим образом. Согласно определению угла между плоскостями, его величина может
быть в пределах от 0 до , т.е. косинус
2
такого угла должен быть положитель-
ным. Поэтому, если |
3a2 4b2 0, |
то |
||
cos cos C NC |
3a2 |
4b2 |
, если |
же |
|
|
|||
1 |
3a2 4b2 |
|
|
|
|
|
|
||
3a2 4b2 0, то
4b2 3a2 cos cos C1NM 3a2 4b2
(поскольку косинусы смежных углов равны по абсолютной величине и противоположны по знаку). Таким образом,
|3a2 4b2 |
окончательно: cos 3a2 4b2 .
|3a2 4b2 |
Ответ: 3a2 4b2 .
Метод параллельных прямых
В некоторых задачах построение линейного угла затруднительно. И тогда вместо линейного угла можно рассмотреть угол с соответственно параллельными сторонами по отношению к линейному углу.
Пример 58. В кубе ABCDABC1 1 1D1 с
ребром, равным a, через точки M на реб-
ре BB и N на DD такие, что BM |
3a |
|
|
||
1 |
1 |
4 |
|
|
|
и DN a , параллельно AC проведена се-
4
кущая плоскость. Определить угол между секущей плоскостью и плоскостью
ABC.
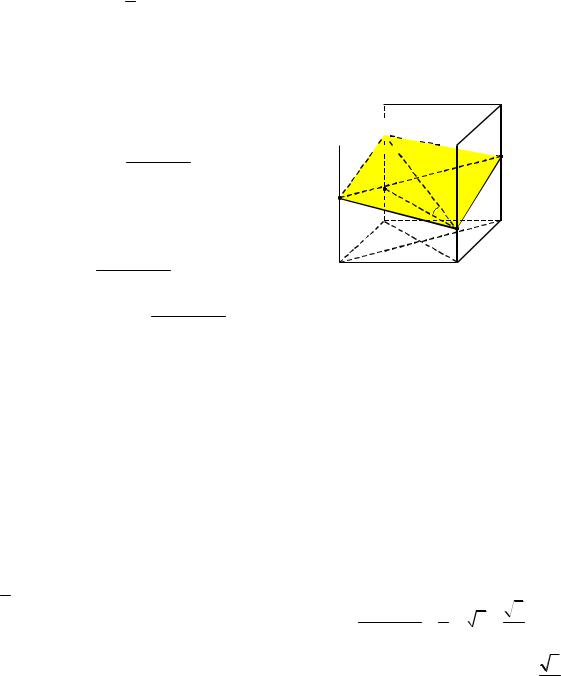
Решение. Построим сечение куба плоскостью, проходящей через точки M и
Nпараллельно AC (см. рис. 68).
Сэтой целью рассмотрим диагональ-
ную плоскость AA1C1 . Соединим точки M
и N, тогда AA1C1 MN O , где точка O –
05.12.2012 |
46 |
середина отрезка MN. Поскольку, согласно условию, секущая плоскость параллельна AC, то прямая l ее пересечения с плоскостью AA1C1 также будет параллельна AC. Поэтому проведем через точку O прямую QP (QP || AC). Соединив последовательно отрезками точки Q, M, P и N, получим сечение QMPN. Так как секущая плоскость пересекает параллельные грани куба по параллельным прямым, то четырехугольник QMPN является параллелограммом.
B1 |
C1 |
A1  M
M D1
D1



 P
P
K |
O |
|
|
Q |
|
B |
C |
|
N |
A D
Рис. 68
В квадрате ABCD диагонали перпендикулярны ( BD AC ), значит, BD l .
Проведем в плоскости BDD1 прямую KN, параллельную BD. Тогда KN l . Прямая BD является проекцией наклонной MN на плоскость АВС, поэтому по теореме о трех перпендикулярах MN l. Прямая MN лежит в плоскости MPNQ, а прямая КN параллельна плоскости ABC . Следовательно, угол KNM равен линейному углу искомого двугранного угла (как углы с соответственно параллельными сторонами).
Пусть MNK , тогда
tg MB ND a :a
 2
2 
 2 .
2 .
BD |
2 |
4 |
Ответ: arctg 2 . 4
Метод параллельных плоскостей
В некоторых задачах является эффективным подход, при котором вместо угла между пересекающимися плоскостями и ищется угол между плоскостями, па-
www.abiturient.ru
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
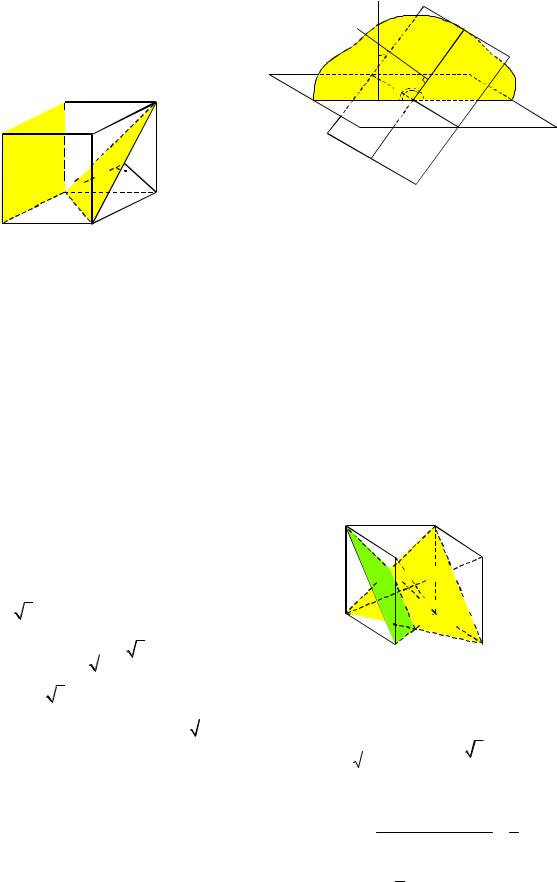
раллельными рассматриваемым (или между одной из данных плоскостей и плоскостью, параллельной другой из них).
Пример 59. В кубе ABCDA1B1C1D1
найти угол между плоскостью грани AABB1 1 и плоскостью BC1D.
B1 C1
A1 D1
D1
 E
E





B


C
A D
Рис. 69
Решение. Так как плоскость AAB1 1 па-
раллельна плоскости DDC1 1 , то искомый угол равен углу между плоскостями BC1D и DDC1 1 (см. рис. 69). Диагонали
грани куба перпендикулярны и точкой пересечения делятся пополам. Поэтому EC DC1 , где точка E – середина от-
резка DC1. Также BE DC1, как высота
равностороннего треугольника BC1D. |
||||||||||||||||||||||
Следовательно, угол BEC есть линейный |
||||||||||||||||||||||
угол двугранного угла BDCC. |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Треугольник |
BEC |
|
|
прямоугольный |
||||||||||||||||||
(BC DDC ) и |
BCE прямой. Пусть |
|||||||||||||||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
тогда BC 1, |
||||||
ребро |
куба |
|
равно 1, |
|||||||||||||||||||
EC |
DC |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
|
|
|
|
|
|
|
|
. Следовательно, |
|||||||||||||
2 |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
2 |
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
tg |
BC |
1: |
|
1 |
|
|
. |
|
|
|||||||||||
|
|
|
2 |
|||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
EC |
2 |
|
|
|
|
|
||||||
Отсюда arctg |
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||
2 |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: arctg |
|
. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
Метод использования перпендикуляров к плоскостям
На рис. |
70 прямые l и l лежат в |
плоскости и перпендикулярны плоско- |
|
стям и |
соответственно. Тогда угол |
между ними равен углу между плоско- |
|
05.12.2012 |
47 |
стями и . В общем случае прямые l
и l могут быть скрещивающимися.
l |
l |
|
|
|
|
|
|||
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 70 |
|
|
Пример |
60. |
В кубе |
ABCDA1B1C1D1 |
|
найти угол между плоскостями AB1C и |
||||
BC1D . |
|
|
|
|
Решение. |
Диагональ |
куба A1C пер- |
||
пендикулярна плоскости BC1D (см. рис.
71), так как A1C BC1 и A1C DC1 (по теореме о трех перпендикулярах). Аналогично диагональ куба BD1 перпендику-
лярна плоскости AB1C . Таким образом, задача сводится к нахождению острого угла между диагоналями A1C и BD1
прямоугольника BCD1A1 .
B1 |
C1 |
A1 |
D1 |



 O
O





 C
C 
B












A
 D
D
Рис. 71
Пусть O – точка пересечения диагоналей и ребро куба равно 1. Тогда
A C BD |
|
|
3 |
. Из тре- |
||
3, OC OB |
||||||
|
||||||
1 |
1 |
2 |
|
|||
|
|
|
||||
угольника ОВС находим
cos BOC OB2 OC2 BC2 1 , 2 OB OC 3
т.е. BOC arccos1. 3
www.abiturient.ru

Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Ответ: arccos1 .
|
|
3 |
|
Пример 61. |
Дан куб ABCDA1B1C1D1 . |
||
Найти угол между плоскостями AB1C1 |
и |
||
A1B1C . |
|
|
|
Решение. Каждая из прямых AD1 |
и |
||
CD1 (см. рис. 72) перпендикулярна плос- |
|||
костям A1B1C |
и AB1C1 соответственно |
||
(докажите самостоятельно). |
|
||
|
|
C1 |
|
B1 |
|
D1 |
|
|
|
|
|
|
A1 |
C |
|
B |
|
D |
|
|
|
|
|
|
A |
|
|
|
Рис. 72 |
|
|
Поэтому величина искомого угла рав- |
|||
на величине угла между прямыми AD1 |
и |
||
CD1 . Так как треугольник AD1C – равно-
сторонний, то получаем ответ: . 3
Ответ: . 3
Пример 62. (МИОО, 2010). Дана пря-
мая четырехугольная призма ABCDA1B1C1D1 , в основании которой лежит прямоугольник ABCD, в котором
AB 5, AD 
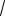 33 . Через середину ребра CD проведена плоскость перпендикулярно прямой B1D. Найти тангенс угла между этой плоскостью и плоскостью грани AA1D1D, если расстояние между прямыми A1C1 и BD равно
33 . Через середину ребра CD проведена плоскость перпендикулярно прямой B1D. Найти тангенс угла между этой плоскостью и плоскостью грани AA1D1D, если расстояние между прямыми A1C1 и BD равно 
 3.
3.
Решение. Так как прямая B1D перпендикулярна проведенной плоскости (на рис. 73 эта плоскость изображена условно), а прямая CD AA1D1 (CD D1D так
как призма и CD AD так как |
ABCD |
прямоугольник), то угол между рассмат- |
|
риваемыми плоскостями равен углу меж- |
|
ду прямыми B1D и CD. |
|
05.12.2012 |
48 |
Тангенс этого угла найдем из прямоугольного треугольника CB1D
(CD AA1D1, следовательно CD B1C). Так как скрещивающиеся прямые A1C1 и BD лежат в параллельных плоскостях, то расстояние между ними равно расстоянию между этими плоскостями. Значит высота и боковое ребро призмы равны
|
|
|
BC2 BB |
2 |
|
||||
|
3. Тогда BC |
6 и ис- |
|||||||
1 |
1 |
|
|||||||
комый тангенс равен |
B1C |
|
6 |
|
1,2. |
||||
|
|
||||||||
|
|
|
|
CD 5 |
|
|
|||
C1
B1

 D1
D1





 A1
A1


 C
C 





B





















 D
D
 A
A
Рис. 73
Ответ: 1,2.
Метод опорных задач
При решении задач этого типа можно
воспользоваться |
|
|
опорными |
задачами |
№ 2, 4, 6 (глава 3 п. 3.4). |
|
|||
Применение «теоремы косинусов |
||||
для трехгранного угла» |
|
|||
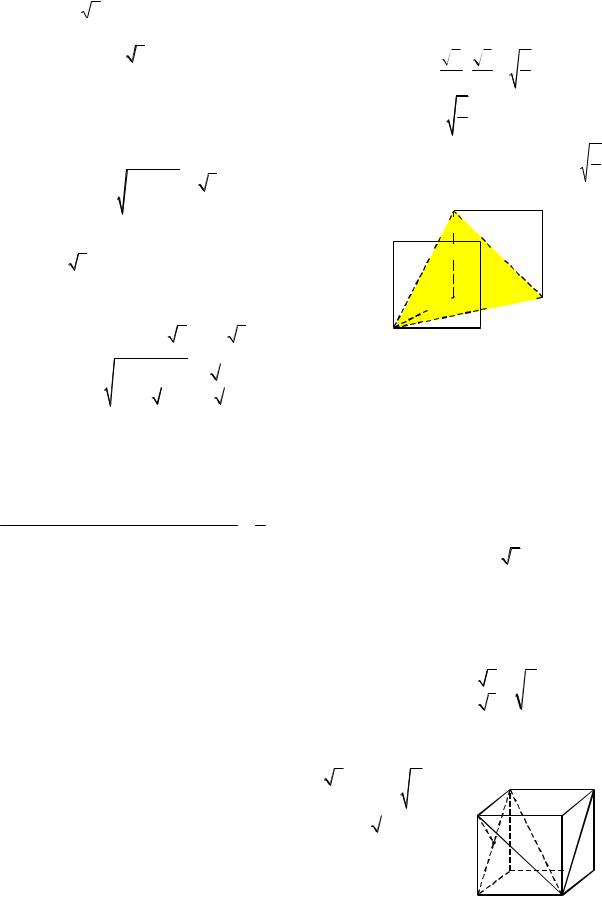
Пример 63. В правильной треугольной |
||||
призме ABCABC |
все рёбра |
равны 1. |
||
1 |
1 |
1 |
|
|
Найти косинус угла между плоскостями
ABC и ABC. |
|
B1 |
C1 |
||||
1 |
|
1 |
1 |
|
|||
Решение. |
Рас- |
|
A1 |
||||
смотрим |
трехгран- |
|
|
||||
ный угол при вер- |
|
||||||
|
|
||||||
шине B1 |
пирамиды |
|
D |
||||
AACB . Обозначим |
|
||||||
B |
C |
||||||
1 |
1 |
|
|
|
|||
|
|
|
|
|
|||
через |
|
|
плоский |
|
A |
||
угол |
двугранного |
|
|||||
угла |
ABCA |
(см. |
|
Рис. 74 |
|||
|
|
1 |
1 |
|
|
|
|
рис. 74). Найдем значения синусов и косинусов плоских углов при вершине B1.
www.abiturient.ru
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
Грань ABB1A1 – квадрат, поэтому
cos AB A |
|
2 |
|
. В треугольнике |
|
ABC |
|||||||||||||||||||||||||||||||||||||||||
2 |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||
AC 1, |
AB1 B1C |
|
|
|
|
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
cos ABC |
|
AB2 |
|
BC2 AC |
2 |
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
2 AB1 B1C |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
2 2 1 |
|
3 |
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 2 |
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3 |
2 |
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|||||||||||||||||||||||
|
sin ABC |
1 |
|
|
|
|
7 |
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
В |
треугольнике |
|
|
|
|
|
|
B AC |
|
|
|
|
|
|
B A 1, |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|||||||||||
AC BC |
|
. Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cos CB1A1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
2 1 2 |
|
|
|
1 |
|
|
|||||||||||||||||||||||||
|
BC B A1 AC |
|
|
|
|
|
|
, |
|||||||||||||||||||||||||||||||||||||||
1 |
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
2 BC B A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
1 |
|
|
2 |
2 |
1 |
|
|
|
2 |
|
2 |
|
||||||||||||||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
. |
|
||||||||||||||||||||||||
|
sin CB A |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
7 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Применяя теорему косинусов для трехгранного угла (опорная задача 2) при вершине B1, получим
cos
cos AB1A1 cos AB1C cos CB1A1 5.
sin AB1C sin CB1A1 |
7 |
Ответ: 5/7.
Применение теоремы «о трех синусах»
Пусть в одной из граней двугранного угла, величина которого равна , проведена прямая, составляющая с ребром двугранного угла угол (0 /2),
– величина угла между этой прямой и другой гранью. Тогда справедливо следующее соотношение:
sin sin sin .
Доказательство этой формулы приведено в главе 3 п. 3.4, опорная задача №4.
Пример 64. В кубе ABCDA1B1C1D1
найдите угол между плоскостями AB1C и АВС.
Решение. Пусть искомый угол.
Так как B1AC 60 , |
B1AB |
05.12.2012 |
49 |
45 (см. рис. 75), то по теореме «о трех синусах» имеем:
sin45 sin sin60 ,
sin 
 2 :
2 : 
 3
3 
 2 . 2 2 3
2 . 2 2 3
Отсюда arcsin 2 . 3
Ответ: arcsin 2 . 3
B1 C1
A1



 D1
D1 
B













 C
C
A D
Рис. 75
Пример 65. Диагональ A1C куба
ABCDA1B1C1D1 служит ребром двугранного угла, грани которого проходят через B1 и D1. Найти величину этого угла.
Решение. Будем считать куб единичным. Пусть Е – середина отрезка A1D, тогда из треугольника A1D1E получаем
sin sin |
|
|
2 |
|
|
|
|
|||||
4 |
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||
( – угол между прямой |
A1D1 |
|
и плоско- |
|||||||||
стью A1B1C ) (см. рис. 76). |
|
|
|
|
|
|||||||
Из треугольника A1D1C находим |
||||||||||||
|
CD1 |
|
|
|
|
|
|
|
|
|
|
|
sin |
|
2 |
|
|
2 |
, |
||||||
|
|
|
|
|
|
3 |
||||||
|
CA1 |
3 |
|
|
|
|
||||||
где – угол между прямой |
|
A1D1 и реб- |
||||||||||
ром A1C двугранного угла. Далее имеем
|
2 |
sin |
|
2 |
, |
A1 |
|||||
2 |
3 |
D1 |
|||||||||
|
|
|
|
|
|
||||||
sin |
|
3 |
|
. |
|
|
|
E |
|||
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
||||
|
Так как точка |
A |
|||||||||
Е (проекция точ- |
|||||||||||
ки D1 |
на |
плос- |
D |
||||||||
B1
C1


 B
B
C
кость |
A1B1C ) |
Рис. 76 |
www.abiturient.ru
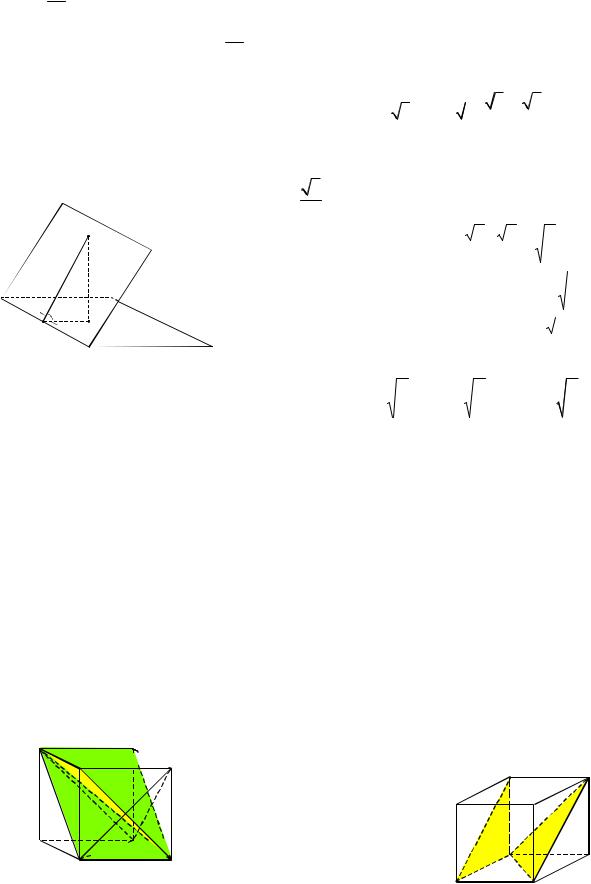
Корянов А.Г., Прокофьев А.А. Многогранники: типы задач и методы их решения.
расположена вне искомого двугранного
угла, то 2 . 3
Ответ: 2 . 3
Использование расстояний от точки до плоскости и до прямой
Решение задач этого пункта основано на применении таких понятий, как расстояние от точки до прямой и расстояние от точки до плоскости.
M
Рис. 77
Пусть даны две плоскости и (см. рис. 77), пересекающиеся по прямой l. Если известны расстояния от точки М, лежащей в плоскости , до плоскости и до прямой l, то угол между плоскостями и можно вычислить, используя
формулу |
|
||
sin ( , ) |
(M, ) |
, |
(7) |
|
|||
|
(M,l) |
|
|
где (M, ) – расстояние от точки М до
плоскости , M,l – расстояние от
точки М до прямой l.
Пример 66. В кубе ABCDA1B1C1D1
найти угол между плоскостями AB1C и A1B1C .
B1 C1
A1 




 D1
D1
B 

 C
C
A D
Рис. 78
05.12.2012
Решение. Пусть сторона куба равна 1. Плоскости AB1C и A1B1C пересекаются по прямой B1C (см. рис. 78). Расстояние от точки А, принадлежащей плоскости AB1C , до прямой B1C равно длине высо-
ты равностороннего треугольника AB1C
со стороной |
|
, т.е. |
|
|
3 |
|
6 |
. Рас- |
|
2 |
2 |
||||||||
2 |
2 |
||||||||
|
|
|
|
|
|
|
стояние от точки А до плоскости A1B1C равно половине диагонали квадрата, т.е.
2 . По формуле (7) имеем
2
sin (ABC, ABC) |
2 |
: |
6 |
|
1 |
. |
|
|
|
|
|
|||||
|
|
|
||||||||||||||
1 |
1 |
1 |
2 |
|
2 |
|
3 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Отсюда искомый угол равен arcsin |
|
|
|
1 |
. |
|||||||||||
3 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
Ответ: arcsin |
|
|
|
. |
|||||||||
|
|
|
|
1/3 |
||||||||||||
Замечание. В зависимости от способа решения ответ может быть записан в разной
форме: arcsin |
1 |
, arccos |
2 |
или arctg |
1 |
. |
|
3 |
2 |
||||
3 |
|
|
|
|||
Использование теоремы о площади ортогональной проекции многоугольника
При применении этого метода угол между плоскостями и можно вычислить, используя формулу
|
|
cos |
Sпр |
, |
(8) |
|
|
|
|
|
|
||||
|
|
|
|
S |
|
|
|
где S |
– площадь многоугольника, лежа- |
|
|||||
щего в плоскости , Sпр – площадь его |
|
||||||
ортогональной проекции на плоскость . |
|
||||||
Пример |
67. В |
кубе |
ABCDA1B1C1D1 |
|
|||
найти угол между плоскостью грани |
|
||||||
AA1B1B и плоскостью BC1D. |
|
||||||
Решение. Пусть ребро куба равно 1. |
|
||||||
Ортогональной |
|
|
|
B1 |
C1 |
||
проекцией |
тре- |
A1 |
D1 |
|
|||
угольника |
BC D |
|
|||||
|
|
1 |
|
|
|
|
|
на |
плоскость |
|
|
|
|
|
|
AA1B1 |
является |
|
|
|
B |
C |
|
треугольник |
|
|
|
|
|||
AB1B |
(см. |
рис. |
A |
D |
|
||
79), площадь ко- |
|
|
|
Рис. 79 |
|
||
|
|
|
|
|
|
|
|
50
www.abiturient.ru
